4.4 平行线的判定方法 课件(共24张PPT) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 4.4 平行线的判定方法 课件(共24张PPT) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 459.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 08:51:43 | ||
图片预览







文档简介
(共24张PPT)
第4章 相交线与平行线
4.4(第1课时) 平行线的判定方法1
学习目标
1.掌握基本事实——同位角相等,两直线平行;(重点)
2.能用三角尺和直尺过已知直线外一点画这条直线的平行线,并能理解这种画法的理论依据.
新课导入
探究
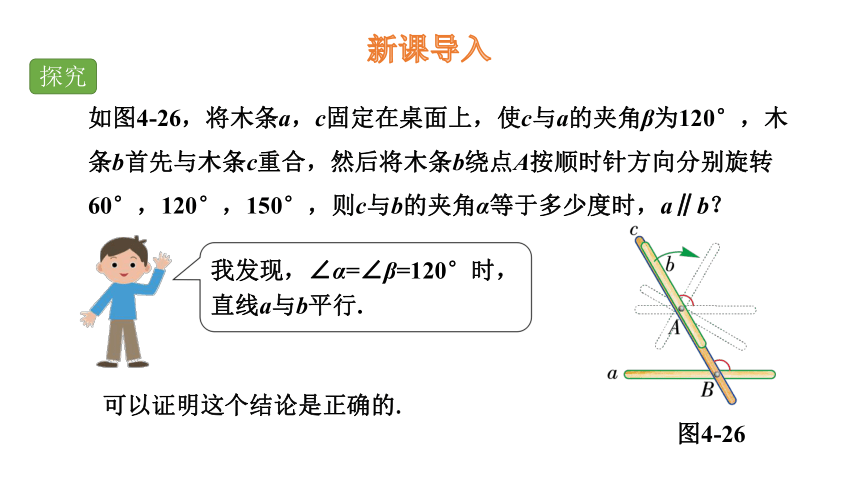
如图4-26,将木条a,c固定在桌面上,使c与a的夹角β为120°,木条b首先与木条c重合,然后将木条b绕点A按顺时针方向分别旋转60°,120°,150°,则c与b的夹角α等于多少度时,a∥b?
我发现,∠α=∠β=120°时,直线a与b平行.
可以证明这个结论是正确的.
图4-26
如图4-27,直线AB,CD被直线EF所截,交于M,N两点,同位角∠α与∠β相等.
过点N作直线PQ∥AB,则∠ENQ=∠α.由于∠α=∠β,因此∠ENQ=∠β,从而射线NQ与射线ND重合,于是直线PQ与直线CD重合.因此CD∥AB.
Q
P
N
M
F
E
D
C
B
A
图4-27
于是,我们有以下基本事实(平行线的判定方法1):
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
通常可以简单地说成:同位角相等,两直线平行.
α
β
在4.1节中,我们学习了一种画平行线的方法(如图4-28),你能说明这种画法的理由吗?
说一说
a
·
P
A
B
C
b
B'
C'
解析:因为三角尺ABC和三角尺A'B'C'是同一把尺子,
所以∠CC'B'=∠ACB,
所以a∥b(同位角相等,两直线平行).
图4-28
【例1】如图4-29,直线 AB,CD被直线EF所截, ∠1+∠2= 180o, AB与CD平行吗?为什么?
解 因为∠1+∠2=180o,而∠3是∠1的补角,
即∠1+∠3=180o,
所以∠2=∠3.
所以 AB∥CD (同位角相等,两直线平行).
1
2
3
A
B
C
D
E
F
图4-29
【例2】如图4-30,直线 a,b被直线c,d所截,∠1=∠2,说明为什么∠4=∠5.
解 因为∠1=∠2 (已知),
∠2=∠3(对顶角相等),
所以∠1=∠3(等量代换) ,
所以a∥b(同位角相等, 两直线平行),
因此∠4=∠5(两直线平行,同位角相等) .
图4-30
a
b
c
d
1
2
3
4
5
练习
1.如图,已知点B、C、D在同一直线上,∠B=∠3,∠2=54°,则∠1=( )
A. 54° B. 36° C. 48° D. 42°
解析:因为∠B=∠3,
所以AB∥CE,
所以∠1=∠2=54°.
A
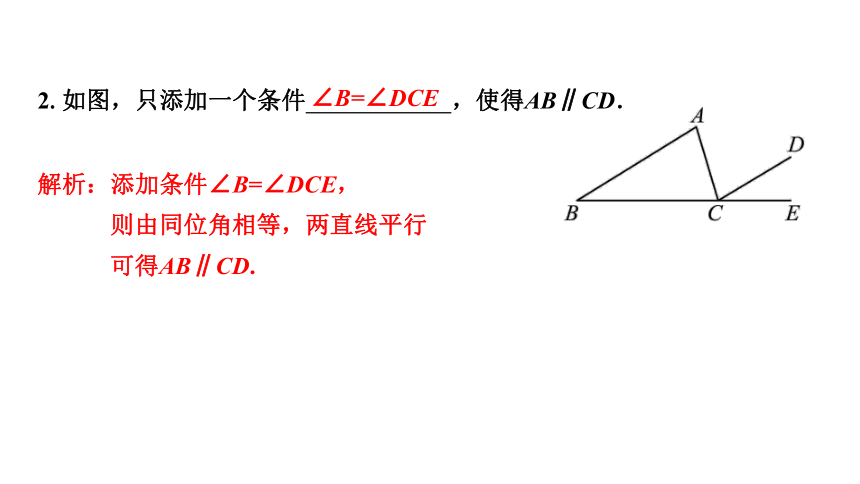
2.如图,只添加一个条件 ,使得AB∥CD.
解析:添加条件∠B=∠DCE,
则由同位角相等,两直线平行
可得AB∥CD.
∠B=∠DCE
3. 如图所示,已知直线EF和AB,CD分别相交于K,H,且∠EGB=90°,∠CHF=60°,∠E=30°,试说明AB∥CD.
解析:因为∠EGB=90° ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°
所以∠AKF=∠CHF,
所以AB∥CD.
4.如图,BDE是一条直线,∠ABD=∠CDE,BF平分∠ABD,DG平分∠CDE,试问BF∥DG吗?为什么?
解析:因为BF平分∠ABD,
所以∠ABF=∠DBF= ∠ABD.
因为DG平分∠CDE,
所以∠CDG=∠EDG= ∠CDE .
因为∠ABD=∠CDE,
所以∠DBF=∠EDG,
所以BF∥DG.
B
A
C
D
E
F
G
课堂小结
由同位角的关系判断两直线平行的三个步骤:
3.得出两条被截直线平行.
2.若相等判断截线和被截直线.
1.判断两个同位角是否相等.
第4章 相交线与平行线
4.4(第2课时) 平行线的判定方法2,3
学习目标
探索并证明平行线的判定方法2,3.(难点)
新课导入
说一说
两条直线被第三条直线所截,由同位角相等可以判定两条直线平行,那么内错角相等可以判定两条直线平行吗?同旁内角互补呢?
由此,我们得到判定两条直线平行的另一种方法:
如图4-31,直线AB,CD被直线EF所截,∠2与∠3是内错角,
已知∠2=∠3,
又因为∠3=∠1(对顶角相等),
所以∠1=∠2.
所以AB∥CD(同位角相等,两直线平行).
F
E
D
C
B
A
图4-31
平行线的判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
通常可以简单地说成:内错角相等,两直线平行.
由此,我们得到判定两条直线平行的第三种方法:
如图4-32,直线AB,CD被直线EF所截,∠1与∠2是同旁内角,
已知∠1+∠2=180°,
又因为∠2+∠3=180°,
所以∠3=∠1.
所以AB∥CD(同位角相等,两直线平行).
F
E
B
A
D
C
图4-32
平行线的判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
通常可以简单地说成:同旁内角互补,两直线平行.
【例3】如图4-33 ,AB∥DC,∠BAD=∠BCD.那么 AD∥BC 吗?
解 因为AB∥DC,
所以∠1=∠2 (两直线平行,内错角相等).
又因为∠BAD=∠BCD,
所以∠BAD-∠1=∠BCD- ∠2.
即∠3=∠4.
所以 AD∥BC(内错角相等,两直线平行).
A
B
C
D
2
1
3
4
图4-33
【例4】如图4-34,∠1=∠2= 50o , AD∥BC, 那么 AB∥DC 吗?
解 因为AD∥BC,
所以∠1 + ∠3 =180°(两直线平行,同旁内角互补).
则∠3 = 180°-∠1=180°- 50°=130° .
所以∠2+∠3 = 50°+130°=180°.
所以 AB∥DC(同旁内角互补,两直线平行).
1
2
3
A
C
D
B
图4-34
练习
1.如图,直线a、b被直线c所截,下列条件中,能判定a∥b的是( )
A. ∠2=∠5 B. ∠3=∠4 C. ∠3+∠4=180° D. ∠4+∠5=180°
解析:A选项∠2=∠5,不能判断ab;
B选项∠3=∠4,不能判断ab;
C选项由∠3+∠4=180°,∠3=∠1得∠1+∠4=180°,
由同旁内角互补,两直线平行,可判断ab;
D选项∠4+∠5=180°,不能判断ab.
C
1
2
3
4
5
a
b
2.如图,点E在AB的延长线上,下列条件中不能判断AD∥BC的是( )
A.∠1=∠3 B.∠2=∠4 C.∠C=∠CBE D. ∠C+∠ABC=180°
解析: 因为∠2=∠4,
所以AD∥CB;
因为∠1=∠3或∠C=∠CBE或∠C+∠ABC=180°,
所以得AB∥DC.
B
3. 如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°则∠ADC=______.
解析:因为∠1=∠2,
所以AB∥DC,
所以∠A+∠ADC=180°,
因为∠A=55°,
所以∠ADC=105°.
105°
4.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠7;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是: .
解析:①∠1=∠7,对顶角相等,不能判定a∥b,①不符合题意;
②∠3=∠6,可根据内错角相等,两直线平行得到a∥b,②符合题意;
③∠1=∠8,根据对顶角∠2=∠8,则∠1=∠2,可由同位角相等,两直线平行得到a∥b,③符合题意;
④∠5+∠8=180°,根据对顶角∠2=∠8、∠3=∠5,可得∠3+∠2=180°,可根据同旁内角互补,两直线平行得到a∥b,④符合题意.
②③④
5.如图,AC∥ED,∠A=∠EDF,若∠FDC=25°,求∠ABC的度数.
解析:因为AC∥DE,
所以∠A=∠DEB.
因为∠A=∠FDE,
所以∠DEB=∠FDE,
所以AB∥DF,
所以∠B=∠FDC=25°.
课堂小结
平行线的判定方法
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
第4章 相交线与平行线
4.4(第1课时) 平行线的判定方法1
学习目标
1.掌握基本事实——同位角相等,两直线平行;(重点)
2.能用三角尺和直尺过已知直线外一点画这条直线的平行线,并能理解这种画法的理论依据.
新课导入
探究
如图4-26,将木条a,c固定在桌面上,使c与a的夹角β为120°,木条b首先与木条c重合,然后将木条b绕点A按顺时针方向分别旋转60°,120°,150°,则c与b的夹角α等于多少度时,a∥b?
我发现,∠α=∠β=120°时,直线a与b平行.
可以证明这个结论是正确的.
图4-26
如图4-27,直线AB,CD被直线EF所截,交于M,N两点,同位角∠α与∠β相等.
过点N作直线PQ∥AB,则∠ENQ=∠α.由于∠α=∠β,因此∠ENQ=∠β,从而射线NQ与射线ND重合,于是直线PQ与直线CD重合.因此CD∥AB.
Q
P
N
M
F
E
D
C
B
A
图4-27
于是,我们有以下基本事实(平行线的判定方法1):
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
通常可以简单地说成:同位角相等,两直线平行.
α
β
在4.1节中,我们学习了一种画平行线的方法(如图4-28),你能说明这种画法的理由吗?
说一说
a
·
P
A
B
C
b
B'
C'
解析:因为三角尺ABC和三角尺A'B'C'是同一把尺子,
所以∠CC'B'=∠ACB,
所以a∥b(同位角相等,两直线平行).
图4-28
【例1】如图4-29,直线 AB,CD被直线EF所截, ∠1+∠2= 180o, AB与CD平行吗?为什么?
解 因为∠1+∠2=180o,而∠3是∠1的补角,
即∠1+∠3=180o,
所以∠2=∠3.
所以 AB∥CD (同位角相等,两直线平行).
1
2
3
A
B
C
D
E
F
图4-29
【例2】如图4-30,直线 a,b被直线c,d所截,∠1=∠2,说明为什么∠4=∠5.
解 因为∠1=∠2 (已知),
∠2=∠3(对顶角相等),
所以∠1=∠3(等量代换) ,
所以a∥b(同位角相等, 两直线平行),
因此∠4=∠5(两直线平行,同位角相等) .
图4-30
a
b
c
d
1
2
3
4
5
练习
1.如图,已知点B、C、D在同一直线上,∠B=∠3,∠2=54°,则∠1=( )
A. 54° B. 36° C. 48° D. 42°
解析:因为∠B=∠3,
所以AB∥CE,
所以∠1=∠2=54°.
A
2.如图,只添加一个条件 ,使得AB∥CD.
解析:添加条件∠B=∠DCE,
则由同位角相等,两直线平行
可得AB∥CD.
∠B=∠DCE
3. 如图所示,已知直线EF和AB,CD分别相交于K,H,且∠EGB=90°,∠CHF=60°,∠E=30°,试说明AB∥CD.
解析:因为∠EGB=90° ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°
所以∠AKF=∠CHF,
所以AB∥CD.
4.如图,BDE是一条直线,∠ABD=∠CDE,BF平分∠ABD,DG平分∠CDE,试问BF∥DG吗?为什么?
解析:因为BF平分∠ABD,
所以∠ABF=∠DBF= ∠ABD.
因为DG平分∠CDE,
所以∠CDG=∠EDG= ∠CDE .
因为∠ABD=∠CDE,
所以∠DBF=∠EDG,
所以BF∥DG.
B
A
C
D
E
F
G
课堂小结
由同位角的关系判断两直线平行的三个步骤:
3.得出两条被截直线平行.
2.若相等判断截线和被截直线.
1.判断两个同位角是否相等.
第4章 相交线与平行线
4.4(第2课时) 平行线的判定方法2,3
学习目标
探索并证明平行线的判定方法2,3.(难点)
新课导入
说一说
两条直线被第三条直线所截,由同位角相等可以判定两条直线平行,那么内错角相等可以判定两条直线平行吗?同旁内角互补呢?
由此,我们得到判定两条直线平行的另一种方法:
如图4-31,直线AB,CD被直线EF所截,∠2与∠3是内错角,
已知∠2=∠3,
又因为∠3=∠1(对顶角相等),
所以∠1=∠2.
所以AB∥CD(同位角相等,两直线平行).
F
E
D
C
B
A
图4-31
平行线的判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
通常可以简单地说成:内错角相等,两直线平行.
由此,我们得到判定两条直线平行的第三种方法:
如图4-32,直线AB,CD被直线EF所截,∠1与∠2是同旁内角,
已知∠1+∠2=180°,
又因为∠2+∠3=180°,
所以∠3=∠1.
所以AB∥CD(同位角相等,两直线平行).
F
E
B
A
D
C
图4-32
平行线的判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
通常可以简单地说成:同旁内角互补,两直线平行.
【例3】如图4-33 ,AB∥DC,∠BAD=∠BCD.那么 AD∥BC 吗?
解 因为AB∥DC,
所以∠1=∠2 (两直线平行,内错角相等).
又因为∠BAD=∠BCD,
所以∠BAD-∠1=∠BCD- ∠2.
即∠3=∠4.
所以 AD∥BC(内错角相等,两直线平行).
A
B
C
D
2
1
3
4
图4-33
【例4】如图4-34,∠1=∠2= 50o , AD∥BC, 那么 AB∥DC 吗?
解 因为AD∥BC,
所以∠1 + ∠3 =180°(两直线平行,同旁内角互补).
则∠3 = 180°-∠1=180°- 50°=130° .
所以∠2+∠3 = 50°+130°=180°.
所以 AB∥DC(同旁内角互补,两直线平行).
1
2
3
A
C
D
B
图4-34
练习
1.如图,直线a、b被直线c所截,下列条件中,能判定a∥b的是( )
A. ∠2=∠5 B. ∠3=∠4 C. ∠3+∠4=180° D. ∠4+∠5=180°
解析:A选项∠2=∠5,不能判断ab;
B选项∠3=∠4,不能判断ab;
C选项由∠3+∠4=180°,∠3=∠1得∠1+∠4=180°,
由同旁内角互补,两直线平行,可判断ab;
D选项∠4+∠5=180°,不能判断ab.
C
1
2
3
4
5
a
b
2.如图,点E在AB的延长线上,下列条件中不能判断AD∥BC的是( )
A.∠1=∠3 B.∠2=∠4 C.∠C=∠CBE D. ∠C+∠ABC=180°
解析: 因为∠2=∠4,
所以AD∥CB;
因为∠1=∠3或∠C=∠CBE或∠C+∠ABC=180°,
所以得AB∥DC.
B
3. 如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°则∠ADC=______.
解析:因为∠1=∠2,
所以AB∥DC,
所以∠A+∠ADC=180°,
因为∠A=55°,
所以∠ADC=105°.
105°
4.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠7;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是: .
解析:①∠1=∠7,对顶角相等,不能判定a∥b,①不符合题意;
②∠3=∠6,可根据内错角相等,两直线平行得到a∥b,②符合题意;
③∠1=∠8,根据对顶角∠2=∠8,则∠1=∠2,可由同位角相等,两直线平行得到a∥b,③符合题意;
④∠5+∠8=180°,根据对顶角∠2=∠8、∠3=∠5,可得∠3+∠2=180°,可根据同旁内角互补,两直线平行得到a∥b,④符合题意.
②③④
5.如图,AC∥ED,∠A=∠EDF,若∠FDC=25°,求∠ABC的度数.
解析:因为AC∥DE,
所以∠A=∠DEB.
因为∠A=∠FDE,
所以∠DEB=∠FDE,
所以AB∥DF,
所以∠B=∠FDC=25°.
课堂小结
平行线的判定方法
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
