4.5(第2课时) 垂线段与点到直线的距离 课件(共18张PPT) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 4.5(第2课时) 垂线段与点到直线的距离 课件(共18张PPT) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 23:51:20 | ||
图片预览






文档简介
(共18张PPT)
第4章 相交线与平行线
4.5(第2课时) 垂线段与点到直线的距离
学习目标
1.了解垂线段最短的性质;(重、难点)
2.理解点到直线的距离的意义;
3.能度量点到直线的距离.
新课导入
做一做
用三角尺或量角器过一点P画已知直线l的垂线,如图4-42.
(1)经过直线l上一点P画l的垂线a;
(2)经过直线l外一点P画l的垂线b.
这样的直线分别可以画出几条呢?
图4-42
假设过点P还有一条直线c⊥l,则c∥a(或c∥b),但是c与a(或b)有公共点P,这是不可能的.
我们有如下基本事实:
如图4-43,设PO垂直于直线l,O为垂足,线段PO叫做点P到直线l的垂线段.经过点P的其他直线交l与A,B,C,D,…,线段PA,PB,PC,PD,…,都不是垂线段,称为斜线段.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
B
A
P
l
O
C
D
图4-43
观察图4-43,PA,PB,PO,PC,PD哪条线段最短?
动脑筋
我发现垂线段PO最短.
如图4-44,用圆规比较垂线段PO和斜线段PA,PB,PC,PD的长度,可知线段PO最短.
由此得出:
直线外一点与直线上各点连接的所有线段中,垂线段最短.
B
A
P
l
O
C
D
图4-44
或者简单地说成:垂线段最短.
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.例如,在图4-43中,垂线段PO的长度叫做点P到直线l的距离.
做一做
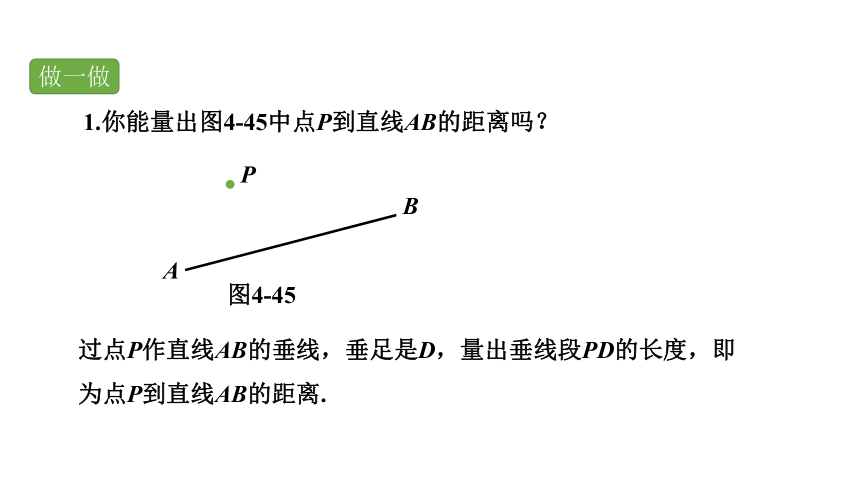
1.你能量出图4-45中点P到直线AB的距离吗?
过点P作直线AB的垂线,垂足是D,量出垂线段PD的长度,即为点P到直线AB的距离.
A
B
P
图4-45
2.如图4-46,某单位要在河岸上l上建一个水泵房饮水到C处,问建在哪个位置才最节省水管?为什么?
过点C作l的垂线,设D为垂足,水泵房应建在D处,因为垂线段最短.
图4-46
我们可以把点到直线的距离转化为点到点的距离.
【例3】如图4-47,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AB=5,BC=12,AC=13.
求:(1)点A到直线BC的距离;
(2)点B到直线AC的距离.
解 (1)因为∠ABC=90°,
所以AB⊥BC,B为垂足.
所以线段AB即为点A到直线BC的垂线段.
因为AB=5,
所以点A到直线BC的距离为5.
图4-47
(2)因为BD⊥AC,垂足为C,
所以线段BD的长度即为点B到直线AC的距离.
因为 ·AB·BC= ·AC·BD,
所以BD= = = .
所以点B到直线AC的距离为 .
练习
1.如图,已知AC⊥BC于点C,CD⊥AB于点D,亮亮总结出了如下结论:
①线段AC的长,表示点A到直线BC的距离;
②线段CD的长,表示点C到直线AB的距离;
③线段AD的长,表示点A到直线CD的距离;
④∠ACD是∠BCD的余角.
亮亮总结的结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
C
2.如图,点P是直线a外一点,过点P作PA⊥a于点A,在直线a上取一点B,连接PB,使PB=PA,C在线段AB上,连接PC.若PA=4,则线段PC的长不可能是( )
A. 3.8 B. 4.9 C. 5.6 D. 5.9
解析:因为过点P作PA⊥a于点A,在直线a上取一点B,连接PB,使PB= PA,C在线段AB上,连接PC.若PA=4,
所以PB=6,
所以4≤PC≤6,故PC不可能是3.8.
A
解析:因为PO⊥AB,
所以PO为垂线段.
因为垂线段最短,
所以PC≥PO.
3.P是直线AB外一点,过点P作PO⊥AB,垂足为O,若C为直线AB上任意一点,则线段PC与线段PO的大小关系是( )
A. PC>PO B. PC < PO C. PC≥PO D. PC≤ PO
C
4. 如图,从直线 l 外一点 P 向 l 引三条线段PA、PB、PC,其中最短的线段为 ,理由是 .
PB
垂线段最短
l
5.一辆汽车在直线形的公路AB上由A向B行驶,C、D 是分别位于公路AB两侧的加油站.
A
B
C
D
M
N
(1)设汽车行驶到公路AB上点M的位置时,距离加油站C最近;行驶到点N的位置时,距离加油站D最近,请在图中分别画出点M、N的位置;
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离C、D两加油站都越来越近?在哪一段路上距离加油站D越来越近,而离加油站C却越来越远?
A
B
C
D
M
N
(2)在公路AB的AM段距离C、D两加油站都越来越近,在MN段距离加油站D越来越近,而离加油站C却越来越远.
课堂小结
垂线的基本事实:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
垂线的性质:
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
第4章 相交线与平行线
4.5(第2课时) 垂线段与点到直线的距离
学习目标
1.了解垂线段最短的性质;(重、难点)
2.理解点到直线的距离的意义;
3.能度量点到直线的距离.
新课导入
做一做
用三角尺或量角器过一点P画已知直线l的垂线,如图4-42.
(1)经过直线l上一点P画l的垂线a;
(2)经过直线l外一点P画l的垂线b.
这样的直线分别可以画出几条呢?
图4-42
假设过点P还有一条直线c⊥l,则c∥a(或c∥b),但是c与a(或b)有公共点P,这是不可能的.
我们有如下基本事实:
如图4-43,设PO垂直于直线l,O为垂足,线段PO叫做点P到直线l的垂线段.经过点P的其他直线交l与A,B,C,D,…,线段PA,PB,PC,PD,…,都不是垂线段,称为斜线段.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
B
A
P
l
O
C
D
图4-43
观察图4-43,PA,PB,PO,PC,PD哪条线段最短?
动脑筋
我发现垂线段PO最短.
如图4-44,用圆规比较垂线段PO和斜线段PA,PB,PC,PD的长度,可知线段PO最短.
由此得出:
直线外一点与直线上各点连接的所有线段中,垂线段最短.
B
A
P
l
O
C
D
图4-44
或者简单地说成:垂线段最短.
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.例如,在图4-43中,垂线段PO的长度叫做点P到直线l的距离.
做一做
1.你能量出图4-45中点P到直线AB的距离吗?
过点P作直线AB的垂线,垂足是D,量出垂线段PD的长度,即为点P到直线AB的距离.
A
B
P
图4-45
2.如图4-46,某单位要在河岸上l上建一个水泵房饮水到C处,问建在哪个位置才最节省水管?为什么?
过点C作l的垂线,设D为垂足,水泵房应建在D处,因为垂线段最短.
图4-46
我们可以把点到直线的距离转化为点到点的距离.
【例3】如图4-47,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AB=5,BC=12,AC=13.
求:(1)点A到直线BC的距离;
(2)点B到直线AC的距离.
解 (1)因为∠ABC=90°,
所以AB⊥BC,B为垂足.
所以线段AB即为点A到直线BC的垂线段.
因为AB=5,
所以点A到直线BC的距离为5.
图4-47
(2)因为BD⊥AC,垂足为C,
所以线段BD的长度即为点B到直线AC的距离.
因为 ·AB·BC= ·AC·BD,
所以BD= = = .
所以点B到直线AC的距离为 .
练习
1.如图,已知AC⊥BC于点C,CD⊥AB于点D,亮亮总结出了如下结论:
①线段AC的长,表示点A到直线BC的距离;
②线段CD的长,表示点C到直线AB的距离;
③线段AD的长,表示点A到直线CD的距离;
④∠ACD是∠BCD的余角.
亮亮总结的结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
C
2.如图,点P是直线a外一点,过点P作PA⊥a于点A,在直线a上取一点B,连接PB,使PB=PA,C在线段AB上,连接PC.若PA=4,则线段PC的长不可能是( )
A. 3.8 B. 4.9 C. 5.6 D. 5.9
解析:因为过点P作PA⊥a于点A,在直线a上取一点B,连接PB,使PB= PA,C在线段AB上,连接PC.若PA=4,
所以PB=6,
所以4≤PC≤6,故PC不可能是3.8.
A
解析:因为PO⊥AB,
所以PO为垂线段.
因为垂线段最短,
所以PC≥PO.
3.P是直线AB外一点,过点P作PO⊥AB,垂足为O,若C为直线AB上任意一点,则线段PC与线段PO的大小关系是( )
A. PC>PO B. PC < PO C. PC≥PO D. PC≤ PO
C
4. 如图,从直线 l 外一点 P 向 l 引三条线段PA、PB、PC,其中最短的线段为 ,理由是 .
PB
垂线段最短
l
5.一辆汽车在直线形的公路AB上由A向B行驶,C、D 是分别位于公路AB两侧的加油站.
A
B
C
D
M
N
(1)设汽车行驶到公路AB上点M的位置时,距离加油站C最近;行驶到点N的位置时,距离加油站D最近,请在图中分别画出点M、N的位置;
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离C、D两加油站都越来越近?在哪一段路上距离加油站D越来越近,而离加油站C却越来越远?
A
B
C
D
M
N
(2)在公路AB的AM段距离C、D两加油站都越来越近,在MN段距离加油站D越来越近,而离加油站C却越来越远.
课堂小结
垂线的基本事实:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
垂线的性质:
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
