4.6 两条平行线之间的距离 课件(共14张ppt) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 4.6 两条平行线之间的距离 课件(共14张ppt) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
第4章 相交线与平行线
4.6 两条平行线间的距离
学习目标
1.了解两条平行线的所有公垂线段都相等;(难点)
2.了解两条平行线之间距离的意义;(重点)
3.能度量两条平行线之间的距离.
新课导入
做一做
我们知道数学课本的对边是互相平行的.请各位同学用刻度尺量一量自己的数学课本,它的宽度是多少?你是怎样量的?
可以把刻度尺放在课本上任何一个位置,但必须保持刻度尺与课本的两边互相垂直,量得的结果是一样的.
通过上面的操作,启发我们猜想:
可以证明这个猜想是对的.
与两条平行直线都垂直的直线,叫做这两条平行直线的
公垂线,这时连接两个垂足的线段(如图4-48中的AB,CD),叫做这两条平行直线的公垂线段.
我们把两条平行的共公垂线段的长度叫做两条平行线间的距离.
两条平行线的所有公垂线段都相等.
D
C
B
A
图4-48
l1
l2
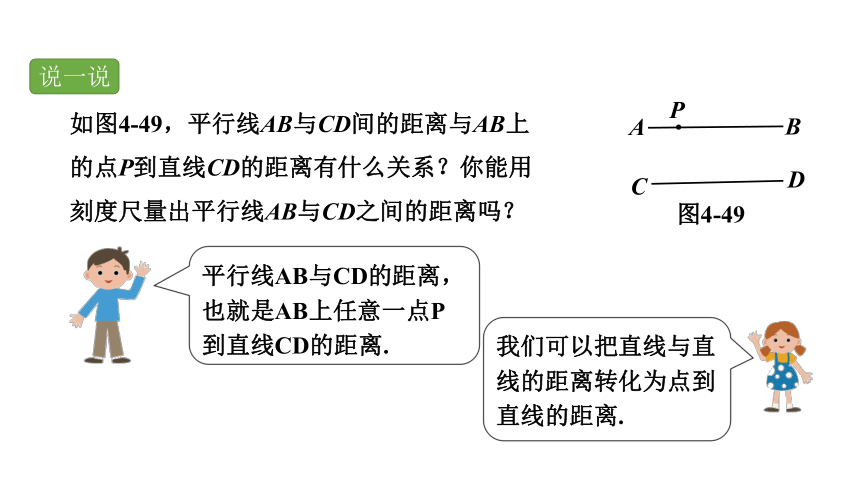
如图4-49,平行线AB与CD间的距离与AB上的点P到直线CD的距离有什么关系?你能用刻度尺量出平行线AB与CD之间的距离吗?
说一说
D
C
B
A
图4-49
P
我们可以把直线与直线的距离转化为点到直线的距离.
平行线AB与CD的距离,也就是AB上任意一点P到直线CD的距离.
【例】如图4-50,设a,b,c是三条互相平行的直线.已知a与b的距离为5 cm,b与c的距离为2 cm,求a与c的距离.
解 在a上任取一点A,过A作AC⊥c,分别与b,c相交于B,C两点.因为a,b,c是三条互相平行的直线,所以∠1=∠2=∠3=90°,即AB⊥b,AC⊥a.因此线段AB,BC,AC分别表示平行线a与b,b与c,a与c的公垂线段.AC=AB+BC=5+2=7(cm),因此a与c的距离是7cm.
A
b
c
B
C
a
5cm
2cm
3
2
1
图4-50
练习
1.已知a∥b,b∥c,且a与b之间的距离为5,b与c之间的距离为3,那么a与c之间的距离为(???????)
A. 2 B. 5 C. 8 D. 2或8
解析:有两种情况:
①如图1
因为AB=5cm, BC=3cm,
所以AC=AB+ BC=8cm.
D
A
B
C
图2
②如图2
因为AB=5cm, BC=3cm, 所以AC=AB-BC=2cm.
c
b
a
图1
A
B
C
b
c
a
2.已知直线m∥n,如图,下列哪条线段的长可以表示直线m与n之间的距离(???????)
A.只有AB B.只有AE C.AB和CD均可 D.AE和CF均可
解析:因为从一条平行线上的任意一点到另一条平行线作垂线,垂线段的长度叫两条平行线之间的距离,
所以线段AB和CD都可以表示直线m与n之间的距离,
C
3. 把直线a沿水平方向平移4cm,平移后的线为直线b,则直线a与直线b之间的距离为(???????)
A.等于4cm B.小于4cm C.大于4cm D.不大于4cm
解析:分两种情况:
如果直线a与水平方向垂直,则直线a与b之间的距离为4cm,
若果直线a与水平方向不垂直, 则直线a与b之间的距离小于4cm
直线a与直线b之间的距离不大于4cm.
D
4.如图所示,直线l1∥l2,点A、B在直线l2上,点C、D在直线l1上,若三角形ABC的面积为S1,三角形ABD的面积为S2,则(??? ??)
A.S1>S2 B.S1=S2 C.S1<S2 D.不确定
解析:因为l1∥l2,
所以C、D两点到l2的距离相等,
即三角形ABC和三角形ABD的高相等.
同时三角形ABC和三角形ABD有共同的底AB,所以它们的面积相等.
B
解析:因为a∥b,
所以三角形ABD的AB边上的高等于三角形ACE的AE边上的高,
因为点B是线段AE的中点,
所以AE=2AB,
所以三角形ACE的面积=三角形ABD的面积×2=2×2=4.
4
5.如图,已知直线a∥b,点B是线段AE的中点,三角形ABD的面积是2,则三角形ACE的面积是______.
6.已知,正方形ABCD的边长为4cm,求三角形EBC的面积.
解析:由题意可知:三角形EBC与正方形ABCD的底相同,都为BC,且三角形EBC的高即是正方形的边DC,
故三角形面积为正方形面积的一半:4×4÷2=8(cm2).
课堂小结
1.两点间的距离:连接两点的线段的长度.
2.点到直线的距离:直线外一点到这条直的垂线段的长度.
3.两平行线间的距离:两条平行线中,一条直线上的点到另一条直线的垂线段的长度。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4.6 两条平行线间的距离
学习目标
1.了解两条平行线的所有公垂线段都相等;(难点)
2.了解两条平行线之间距离的意义;(重点)
3.能度量两条平行线之间的距离.
新课导入
做一做
我们知道数学课本的对边是互相平行的.请各位同学用刻度尺量一量自己的数学课本,它的宽度是多少?你是怎样量的?
可以把刻度尺放在课本上任何一个位置,但必须保持刻度尺与课本的两边互相垂直,量得的结果是一样的.
通过上面的操作,启发我们猜想:
可以证明这个猜想是对的.
与两条平行直线都垂直的直线,叫做这两条平行直线的
公垂线,这时连接两个垂足的线段(如图4-48中的AB,CD),叫做这两条平行直线的公垂线段.
我们把两条平行的共公垂线段的长度叫做两条平行线间的距离.
两条平行线的所有公垂线段都相等.
D
C
B
A
图4-48
l1
l2
如图4-49,平行线AB与CD间的距离与AB上的点P到直线CD的距离有什么关系?你能用刻度尺量出平行线AB与CD之间的距离吗?
说一说
D
C
B
A
图4-49
P
我们可以把直线与直线的距离转化为点到直线的距离.
平行线AB与CD的距离,也就是AB上任意一点P到直线CD的距离.
【例】如图4-50,设a,b,c是三条互相平行的直线.已知a与b的距离为5 cm,b与c的距离为2 cm,求a与c的距离.
解 在a上任取一点A,过A作AC⊥c,分别与b,c相交于B,C两点.因为a,b,c是三条互相平行的直线,所以∠1=∠2=∠3=90°,即AB⊥b,AC⊥a.因此线段AB,BC,AC分别表示平行线a与b,b与c,a与c的公垂线段.AC=AB+BC=5+2=7(cm),因此a与c的距离是7cm.
A
b
c
B
C
a
5cm
2cm
3
2
1
图4-50
练习
1.已知a∥b,b∥c,且a与b之间的距离为5,b与c之间的距离为3,那么a与c之间的距离为(???????)
A. 2 B. 5 C. 8 D. 2或8
解析:有两种情况:
①如图1
因为AB=5cm, BC=3cm,
所以AC=AB+ BC=8cm.
D
A
B
C
图2
②如图2
因为AB=5cm, BC=3cm, 所以AC=AB-BC=2cm.
c
b
a
图1
A
B
C
b
c
a
2.已知直线m∥n,如图,下列哪条线段的长可以表示直线m与n之间的距离(???????)
A.只有AB B.只有AE C.AB和CD均可 D.AE和CF均可
解析:因为从一条平行线上的任意一点到另一条平行线作垂线,垂线段的长度叫两条平行线之间的距离,
所以线段AB和CD都可以表示直线m与n之间的距离,
C
3. 把直线a沿水平方向平移4cm,平移后的线为直线b,则直线a与直线b之间的距离为(???????)
A.等于4cm B.小于4cm C.大于4cm D.不大于4cm
解析:分两种情况:
如果直线a与水平方向垂直,则直线a与b之间的距离为4cm,
若果直线a与水平方向不垂直, 则直线a与b之间的距离小于4cm
直线a与直线b之间的距离不大于4cm.
D
4.如图所示,直线l1∥l2,点A、B在直线l2上,点C、D在直线l1上,若三角形ABC的面积为S1,三角形ABD的面积为S2,则(??? ??)
A.S1>S2 B.S1=S2 C.S1<S2 D.不确定
解析:因为l1∥l2,
所以C、D两点到l2的距离相等,
即三角形ABC和三角形ABD的高相等.
同时三角形ABC和三角形ABD有共同的底AB,所以它们的面积相等.
B
解析:因为a∥b,
所以三角形ABD的AB边上的高等于三角形ACE的AE边上的高,
因为点B是线段AE的中点,
所以AE=2AB,
所以三角形ACE的面积=三角形ABD的面积×2=2×2=4.
4
5.如图,已知直线a∥b,点B是线段AE的中点,三角形ABD的面积是2,则三角形ACE的面积是______.
6.已知,正方形ABCD的边长为4cm,求三角形EBC的面积.
解析:由题意可知:三角形EBC与正方形ABCD的底相同,都为BC,且三角形EBC的高即是正方形的边DC,
故三角形面积为正方形面积的一半:4×4÷2=8(cm2).
课堂小结
1.两点间的距离:连接两点的线段的长度.
2.点到直线的距离:直线外一点到这条直的垂线段的长度.
3.两平行线间的距离:两条平行线中,一条直线上的点到另一条直线的垂线段的长度。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
