5.1 轴对称 课件(2课时,共22张PPT) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 5.1 轴对称 课件(2课时,共22张PPT) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 562.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
第5章 轴对称与旋转
5.1.1 轴对称图形
学习目标
1.引导学生从生活中的图形入手,去感受对称的和谐美,从而引出轴对称图形的概念;
2.通过具体实例了解轴对称的概念,探究它的基本性质;(重、难点)
新课导入
观察
观察图5-1中的一组生肖剪纸,你能发现它们有什么共同的特征吗?
若将图5-1中的每个图形沿虚线对折,虚线两侧的部分能够完全重合.
图5-1
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
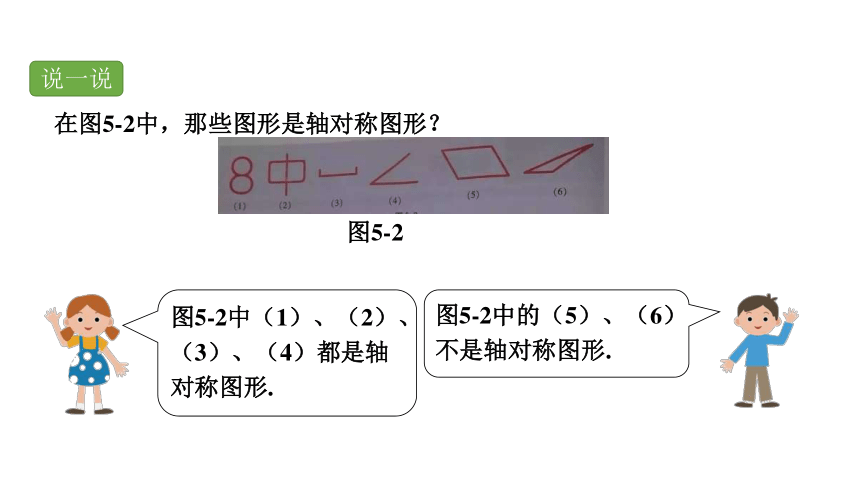
在图5-2中,那些图形是轴对称图形?
说一说
图5-2中(1)、(2)、(3)、(4)都是轴对称图形.
图5-2中的(5)、(6)不是轴对称图形.
图5-2
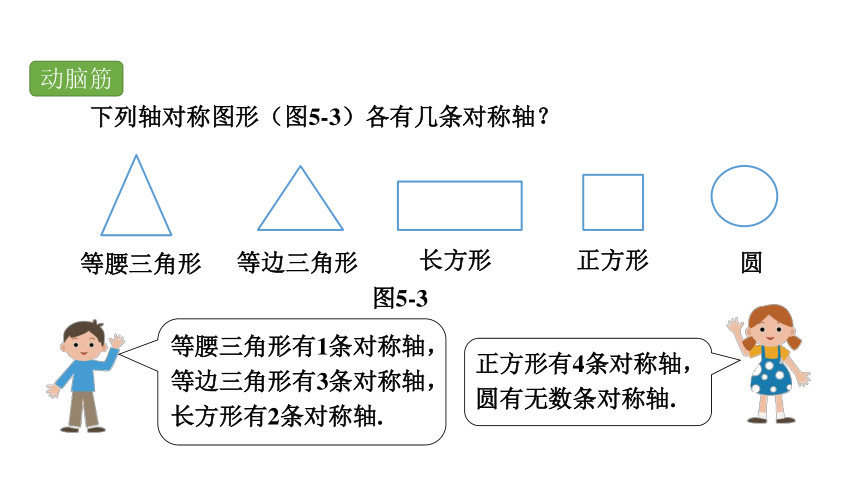
下列轴对称图形(图5-3)各有几条对称轴?
图5-3
动脑筋
等腰三角形
等边三角形
长方形
正方形
圆
等腰三角形有1条对称轴,等边三角形有3条对称轴,长方形有2条对称轴.
正方形有4条对称轴,
圆有无数条对称轴.
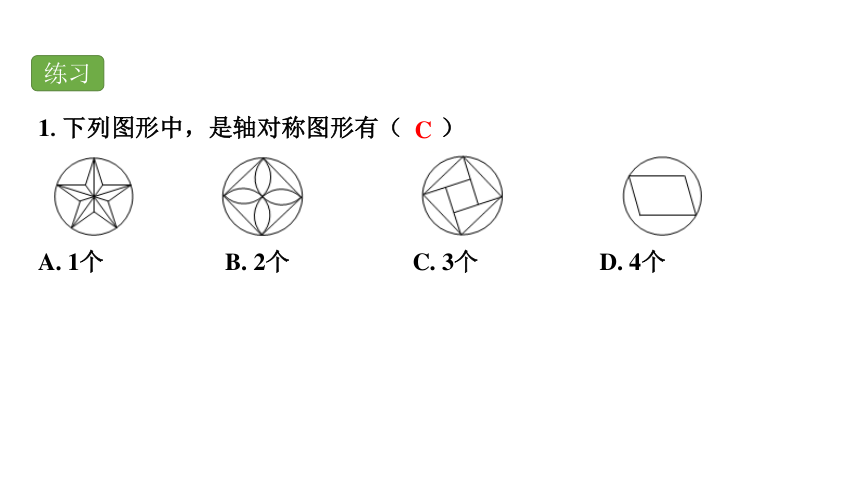
练习
1.下列图形中,是轴对称图形有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
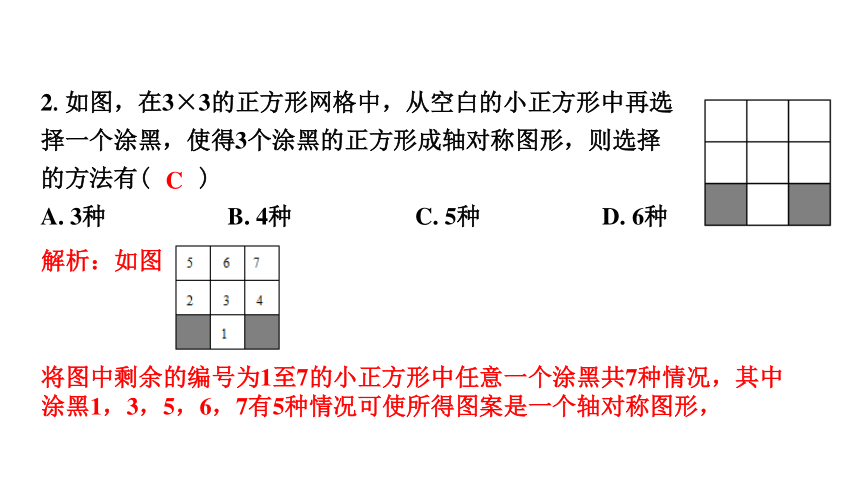
2.如图,在3×3的正方形网格中,从空白的小正方形中再选择一个涂黑,使得3个涂黑的正方形成轴对称图形,则选择的方法有( )
A. 3种 B. 4种 C. 5种 D. 6种
C
解析:如图
将图中剩余的编号为1至7的小正方形中任意一个涂黑共7种情况,其中涂黑1,3,5,6,7有5种情况可使所得图案是一个轴对称图形,
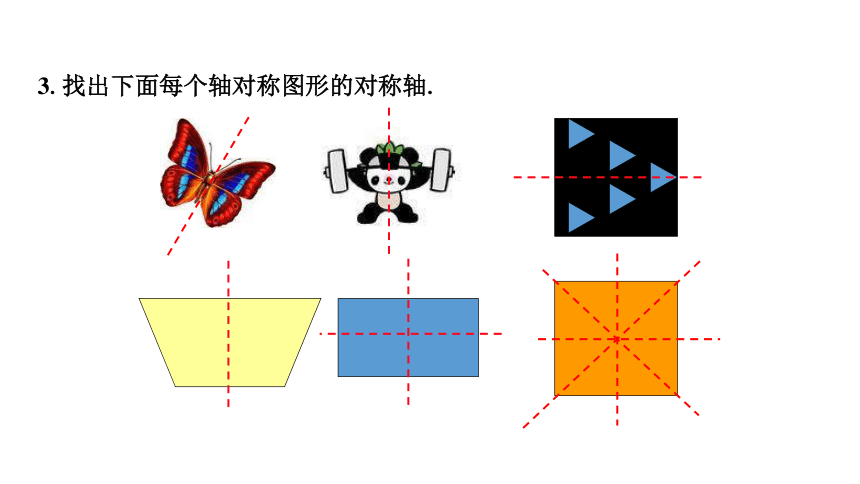
3.找出下面每个轴对称图形的对称轴.
课堂小结
轴对称图形
定义
现象
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
一个图形具有的特殊形状.
第5章 轴对称与旋转
5.1.2 轴对称变换
学习目标
1.能画出简单平面图形(点、线段、直线、三角形)关于给定对称轴的对称图形;(重、难点)
2.能认识并会欣赏自然界和现实生活中的轴对称图形;
3.要培养学生的动手操作能力和合情推理能力.
新课导入
观察
如图5-4,用印章在一张纸上盖一个印(a),趁印迹未干之时,将纸张沿着直线l对折,得到印(b),随后打开,观察图形(a)与图形(b)有怎样的关系.
图5-4
把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换,也叫轴反射.图形(a)叫做原像,图形(b)叫做图形(a)在这个轴反射下的像.
(a)
(b)
如果一个图形关于某一条直线作轴对称变换后,能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称这两个图形成轴对称.这条直线叫做对称轴.原像与像中能互相重合的两个点,其中一点叫做另一个点关于这条直线的对应点.
例如图5-4中点A'叫做点A的对应点.
图5-4中,对称轴l两边的图形(a)与(b)的形状和大小发生变化了吗?
说一说
轴对称变换具有下述性质:
轴对称变换不改变图形的形状与大小.
图形经过轴对称变换,长度、角度和面积等都不改变.
在图5-5中,三角形ABC和三角形A'B'C'关于直线l成轴对称,点P和P'是对应点,线段PP′交直线l于点D.那么线段PP′与对称轴l有什么关系呢?
图5-5
探究
因为三角形ABC和三角形A'B'C'关于直线l成轴对称,将图5-5沿直线l折叠,则点P与P'重合,所以PD与P'D,∠1与∠2也互相重合,故有PD=P'D,∠1=∠2=90°,因此,l⊥PP',且平分PP',即直线l垂直平分线段PP'.
因此得到下面的性质:
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
从图5-5可以看出,如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
【例1】如图5-6,已知直线 l 及直线外一点P,求作点P',使它与点P关于直线l对称.
作法: 1. 过点P作 PQ⊥l,交l于点O.
2. 在直线 PQ上,截取 OP'=OP.
则点P'即为所求作的点.
.
P
O
P'
l
Q
如图5-7,已知线段AB和直线 l ,作出与线段AB关于直线l对称的图形.
图5-7
做一做
l
A
B
A'
B'
)
)
【例2】如图5-8,已知三角形ABC和直线l,作出与三角形 ABC关于直线 l 对称的图形.
作法: 1. 过点A作直线 l 的垂线,垂足为点O,在垂线上截取OA'=OA,点A'就是点A关于直线 l 的对应点.
2. 类似地,分别作出点B,C关于直线 l 的对应点 B',C'.
分析 要作三角形ABC关于直线 l 的对称图形,只要作出三角形的顶点A,B,C关于直线 l 的对应点A',B',C',连接这些对应点,得到的三角形A'B'C'就是三角形ABC 关于直线 l 对称的图形.
3. 连接A'B',B'C',C'A'得到的三角形A'B'C'即为所求.
l
A
C
A'
B'
C'
O
B
图5-8
练习
1.已知线段AB,求作线段CD,使它与线段AB关于直线 l 对称.
A
B
l
l
A
B
A
B
l
C
(D)
C
D
C
D
2.把下列图形补成关于直线 l 对称的图形.
l
l
l
3.请画出三角形ABC关于直线 l 对称的三角形A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法,保留作图痕迹).
l
A
B
C
A'
B'
C'
课堂小结
轴对称变换
性质1
性质2
轴对称变换不改变图形的形状与大小.
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
第5章 轴对称与旋转
5.1.1 轴对称图形
学习目标
1.引导学生从生活中的图形入手,去感受对称的和谐美,从而引出轴对称图形的概念;
2.通过具体实例了解轴对称的概念,探究它的基本性质;(重、难点)
新课导入
观察
观察图5-1中的一组生肖剪纸,你能发现它们有什么共同的特征吗?
若将图5-1中的每个图形沿虚线对折,虚线两侧的部分能够完全重合.
图5-1
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
在图5-2中,那些图形是轴对称图形?
说一说
图5-2中(1)、(2)、(3)、(4)都是轴对称图形.
图5-2中的(5)、(6)不是轴对称图形.
图5-2
下列轴对称图形(图5-3)各有几条对称轴?
图5-3
动脑筋
等腰三角形
等边三角形
长方形
正方形
圆
等腰三角形有1条对称轴,等边三角形有3条对称轴,长方形有2条对称轴.
正方形有4条对称轴,
圆有无数条对称轴.
练习
1.下列图形中,是轴对称图形有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
2.如图,在3×3的正方形网格中,从空白的小正方形中再选择一个涂黑,使得3个涂黑的正方形成轴对称图形,则选择的方法有( )
A. 3种 B. 4种 C. 5种 D. 6种
C
解析:如图
将图中剩余的编号为1至7的小正方形中任意一个涂黑共7种情况,其中涂黑1,3,5,6,7有5种情况可使所得图案是一个轴对称图形,
3.找出下面每个轴对称图形的对称轴.
课堂小结
轴对称图形
定义
现象
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
一个图形具有的特殊形状.
第5章 轴对称与旋转
5.1.2 轴对称变换
学习目标
1.能画出简单平面图形(点、线段、直线、三角形)关于给定对称轴的对称图形;(重、难点)
2.能认识并会欣赏自然界和现实生活中的轴对称图形;
3.要培养学生的动手操作能力和合情推理能力.
新课导入
观察
如图5-4,用印章在一张纸上盖一个印(a),趁印迹未干之时,将纸张沿着直线l对折,得到印(b),随后打开,观察图形(a)与图形(b)有怎样的关系.
图5-4
把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换,也叫轴反射.图形(a)叫做原像,图形(b)叫做图形(a)在这个轴反射下的像.
(a)
(b)
如果一个图形关于某一条直线作轴对称变换后,能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称这两个图形成轴对称.这条直线叫做对称轴.原像与像中能互相重合的两个点,其中一点叫做另一个点关于这条直线的对应点.
例如图5-4中点A'叫做点A的对应点.
图5-4中,对称轴l两边的图形(a)与(b)的形状和大小发生变化了吗?
说一说
轴对称变换具有下述性质:
轴对称变换不改变图形的形状与大小.
图形经过轴对称变换,长度、角度和面积等都不改变.
在图5-5中,三角形ABC和三角形A'B'C'关于直线l成轴对称,点P和P'是对应点,线段PP′交直线l于点D.那么线段PP′与对称轴l有什么关系呢?
图5-5
探究
因为三角形ABC和三角形A'B'C'关于直线l成轴对称,将图5-5沿直线l折叠,则点P与P'重合,所以PD与P'D,∠1与∠2也互相重合,故有PD=P'D,∠1=∠2=90°,因此,l⊥PP',且平分PP',即直线l垂直平分线段PP'.
因此得到下面的性质:
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
从图5-5可以看出,如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
【例1】如图5-6,已知直线 l 及直线外一点P,求作点P',使它与点P关于直线l对称.
作法: 1. 过点P作 PQ⊥l,交l于点O.
2. 在直线 PQ上,截取 OP'=OP.
则点P'即为所求作的点.
.
P
O
P'
l
Q
如图5-7,已知线段AB和直线 l ,作出与线段AB关于直线l对称的图形.
图5-7
做一做
l
A
B
A'
B'
)
)
【例2】如图5-8,已知三角形ABC和直线l,作出与三角形 ABC关于直线 l 对称的图形.
作法: 1. 过点A作直线 l 的垂线,垂足为点O,在垂线上截取OA'=OA,点A'就是点A关于直线 l 的对应点.
2. 类似地,分别作出点B,C关于直线 l 的对应点 B',C'.
分析 要作三角形ABC关于直线 l 的对称图形,只要作出三角形的顶点A,B,C关于直线 l 的对应点A',B',C',连接这些对应点,得到的三角形A'B'C'就是三角形ABC 关于直线 l 对称的图形.
3. 连接A'B',B'C',C'A'得到的三角形A'B'C'即为所求.
l
A
C
A'
B'
C'
O
B
图5-8
练习
1.已知线段AB,求作线段CD,使它与线段AB关于直线 l 对称.
A
B
l
l
A
B
A
B
l
C
(D)
C
D
C
D
2.把下列图形补成关于直线 l 对称的图形.
l
l
l
3.请画出三角形ABC关于直线 l 对称的三角形A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法,保留作图痕迹).
l
A
B
C
A'
B'
C'
课堂小结
轴对称变换
性质1
性质2
轴对称变换不改变图形的形状与大小.
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
