6.1.2 中位数 课件(共15张ppt) 2023-2024学年数学湘教版七年级下册
文档属性
| 名称 | 6.1.2 中位数 课件(共15张ppt) 2023-2024学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 923.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
第6章 数据的分析
6.1.2 中位数
学习目标
1.理解中位数的意义,知道它是一组数据的代表值;
2.会计算一组数据的中位数;(重点)
3.理解中位数的统计意义及它在实际问题中的具体含义.(重、难点)
新课导入
动脑筋
张某管理一家餐馆,下面是该餐馆所有工作人员在2010年10月的工资情况:
张某:15000元; 会计:1800元;
厨师甲:2500元; 厨师乙:2000元;
杂工甲:1000元; 杂工乙:1000元;
服务员甲:1500元; 服务员乙:1200元;
服务员丙:1000元.
计算他们的平均工资,这个平均工资能反映该餐馆员工在这个月收入的一般水平吗?
设餐馆全体员工的平均工资为 ,则(可用计算器计算)
实际上,3000元不能代表餐馆员工在这个月收入的一般水平,因为员工中除张某外工资最高的厨师甲的月收入2500元都小于这个平均数.
=
=3000(元)
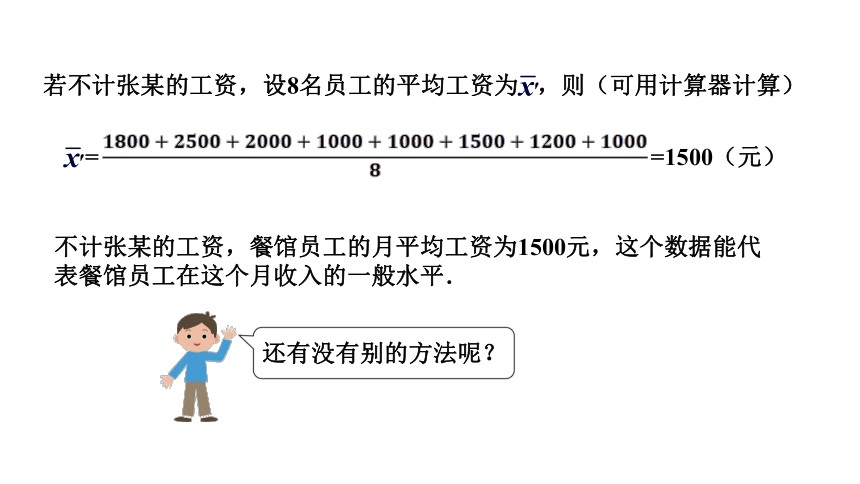
若不计张某的工资,设8名员工的平均工资为 ,则(可用计算器计算)
还有没有别的方法呢?
'
'
= =1500(元)
不计张某的工资,餐馆员工的月平均工资为1500元,这个数据能代表餐馆员工在这个月收入的一般水平.
我们可以把餐馆中人员的月收入按从小到大的顺序排列:
位于中间的数据,即第5个数据为1500,它能比较合理地反映该餐馆员工的月收入水平.
像上述例子那样,把一组数据从小到大的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数.如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数.
1000,1 000,1000,1200,1500,1800,2000,2500,15000.
【例3】求下列两组数据的中位数:
(1)14,11,13,10,17,16,28;
(2)453,442,450,445,446,457,448,449,451,450.
解 (1)把这组数据从小到大排列:
10,11,13,14,16,17,28.
位于中间的数是14,因此这组数据的中位数是14.
(2)把这组数据从小到大排列:
442,445,446,448,449,450,450,451,453,457.
位于中间的两个数是449和450,这两个数的平均数是 449.5,因此这组数据的中位数是449.5.
中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数.因此,中位数常用来描述“中间位置”或“中等水平”,但中位数没有利用数据组中所有的信息.
练习
B
1.某学校七年级一班六名同学定点投篮测试,每人投篮5次,投中的次数统计如下:4,2,3,4,3,2.这组数据的中位数是( )
A. 2 B. 3 C. 4 D. 3.5
解析:把这组数据从小到大排列:
2,2,3,3,4,4.
位于中间的两个数是3和3,这两个数的平均数是3,因此这组数据的中位数是3.
C
解析:把这组数据从小到大排列:120,120,150,150,150,210,210,210,210,210,260,260,260,510,1800.
位于中间的数是210,所以这15人该月销售量的中位数是210.
2.某公司销售部有营销人员15人,统计了某月的销售量,如表所示:
则这15人该月销售量的中位数是(???????)
A. 260 B. 235 C. 210 D. 175
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每人销售量/件
1800
510
260
210
150
120
人数
1
1
3
5
3
2
3.某班五个合作学习小组人数如下:5,5,x,6,7,已知这组数据的平均数是6,则这组数据的中位数是________.
解析:由平均数是6可以求出x=7,
所以把这组数据从小到大排列:
5,5,6,7,7.
位于中间的数是6,因此这组数据的中位数是6.
6
4. 若数据x,1,2,2,5,6,7,8的中位数是4.5,则x的值是________.
解析:因为1,2,2,5,6,7,8的中位数是3.5,
所以2<x<5,
所以1,2,2,x,5,6,7,8的中位数是4.5,
即(x+5)÷2=4.5,
所以x=4.
4
5. 某车间工人日加工零件数如下表:
解析:把这些数据从小到大排列:
5,5,6,6,6,7,7,7,7,8,8,9.
位于中间的两个数是6和6,这两个数的平均数是6,因此这些工人日加工零件数的中位数是6.
意义: 可以估计, 小于或大于这个中位数的零件数的工人各占一半.
件数
5
6
7
8
9
人数
2
3
4
2
1
这些工人日加工零件数的中位数是多少?说明这个中位数的意义.
6. 中央电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示.选手得分的中位数是多少?
解析:按得分情况列表如下:
把这些数据从小到大排列:5,5,10,10,10,10,10,10,10,10,15,15,15,15,
15,15,20,20,20,20.位于中间的两个数是10和15,这两个数的平均数是12.5,因此选手得分的中位数是12.5.
得分
5
10
15
20
人数
2
8
6
4
课堂小结
中位数的意义:中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数,因此,在一定意义上,中位数代表了一组数据的“中点”.
注意:中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是这组数据中的数据.
求中位数的方法:先将数据按一定的顺序排列,若这组数据是奇数个,则中间的数据是中位数;若这组数据是偶数个时,则中间的两个数据的平均数是中位数.
6.1.2 中位数
学习目标
1.理解中位数的意义,知道它是一组数据的代表值;
2.会计算一组数据的中位数;(重点)
3.理解中位数的统计意义及它在实际问题中的具体含义.(重、难点)
新课导入
动脑筋
张某管理一家餐馆,下面是该餐馆所有工作人员在2010年10月的工资情况:
张某:15000元; 会计:1800元;
厨师甲:2500元; 厨师乙:2000元;
杂工甲:1000元; 杂工乙:1000元;
服务员甲:1500元; 服务员乙:1200元;
服务员丙:1000元.
计算他们的平均工资,这个平均工资能反映该餐馆员工在这个月收入的一般水平吗?
设餐馆全体员工的平均工资为 ,则(可用计算器计算)
实际上,3000元不能代表餐馆员工在这个月收入的一般水平,因为员工中除张某外工资最高的厨师甲的月收入2500元都小于这个平均数.
=
=3000(元)
若不计张某的工资,设8名员工的平均工资为 ,则(可用计算器计算)
还有没有别的方法呢?
'
'
= =1500(元)
不计张某的工资,餐馆员工的月平均工资为1500元,这个数据能代表餐馆员工在这个月收入的一般水平.
我们可以把餐馆中人员的月收入按从小到大的顺序排列:
位于中间的数据,即第5个数据为1500,它能比较合理地反映该餐馆员工的月收入水平.
像上述例子那样,把一组数据从小到大的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数.如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数.
1000,1 000,1000,1200,1500,1800,2000,2500,15000.
【例3】求下列两组数据的中位数:
(1)14,11,13,10,17,16,28;
(2)453,442,450,445,446,457,448,449,451,450.
解 (1)把这组数据从小到大排列:
10,11,13,14,16,17,28.
位于中间的数是14,因此这组数据的中位数是14.
(2)把这组数据从小到大排列:
442,445,446,448,449,450,450,451,453,457.
位于中间的两个数是449和450,这两个数的平均数是 449.5,因此这组数据的中位数是449.5.
中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数.因此,中位数常用来描述“中间位置”或“中等水平”,但中位数没有利用数据组中所有的信息.
练习
B
1.某学校七年级一班六名同学定点投篮测试,每人投篮5次,投中的次数统计如下:4,2,3,4,3,2.这组数据的中位数是( )
A. 2 B. 3 C. 4 D. 3.5
解析:把这组数据从小到大排列:
2,2,3,3,4,4.
位于中间的两个数是3和3,这两个数的平均数是3,因此这组数据的中位数是3.
C
解析:把这组数据从小到大排列:120,120,150,150,150,210,210,210,210,210,260,260,260,510,1800.
位于中间的数是210,所以这15人该月销售量的中位数是210.
2.某公司销售部有营销人员15人,统计了某月的销售量,如表所示:
则这15人该月销售量的中位数是(???????)
A. 260 B. 235 C. 210 D. 175
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每人销售量/件
1800
510
260
210
150
120
人数
1
1
3
5
3
2
3.某班五个合作学习小组人数如下:5,5,x,6,7,已知这组数据的平均数是6,则这组数据的中位数是________.
解析:由平均数是6可以求出x=7,
所以把这组数据从小到大排列:
5,5,6,7,7.
位于中间的数是6,因此这组数据的中位数是6.
6
4. 若数据x,1,2,2,5,6,7,8的中位数是4.5,则x的值是________.
解析:因为1,2,2,5,6,7,8的中位数是3.5,
所以2<x<5,
所以1,2,2,x,5,6,7,8的中位数是4.5,
即(x+5)÷2=4.5,
所以x=4.
4
5. 某车间工人日加工零件数如下表:
解析:把这些数据从小到大排列:
5,5,6,6,6,7,7,7,7,8,8,9.
位于中间的两个数是6和6,这两个数的平均数是6,因此这些工人日加工零件数的中位数是6.
意义: 可以估计, 小于或大于这个中位数的零件数的工人各占一半.
件数
5
6
7
8
9
人数
2
3
4
2
1
这些工人日加工零件数的中位数是多少?说明这个中位数的意义.
6. 中央电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示.选手得分的中位数是多少?
解析:按得分情况列表如下:
把这些数据从小到大排列:5,5,10,10,10,10,10,10,10,10,15,15,15,15,
15,15,20,20,20,20.位于中间的两个数是10和15,这两个数的平均数是12.5,因此选手得分的中位数是12.5.
得分
5
10
15
20
人数
2
8
6
4
课堂小结
中位数的意义:中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数,因此,在一定意义上,中位数代表了一组数据的“中点”.
注意:中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是这组数据中的数据.
求中位数的方法:先将数据按一定的顺序排列,若这组数据是奇数个,则中间的数据是中位数;若这组数据是偶数个时,则中间的两个数据的平均数是中位数.
