人教版五年级数学下册 质数和合数复习课件(共28张ppt)
文档属性
| 名称 | 人教版五年级数学下册 质数和合数复习课件(共28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 649.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
质数和合数 复习
100以内质数表:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
填 空:
(1) 一个数除了( )和它的( ),不再有别的因数,这个数叫做( )数。
(2) 一个数除了( )和它的( ),还有别的因数,这个数叫做( )数。
(3) ( )不是质数,也不是合数。
(4)末尾是( )的整数是2的倍数: 末尾是( )的数是5的倍数,( )的数是3的倍数 。
1
本身
质
1
本身
合
1
0,2,4,6,8
0或5
各位上的数字的和能被3整除
(5)最小的质数是( ),最小的合数是( ),最小的偶数是( ),最小的奇数是( )。
(6)判断一个数是质数或合数的方法是根据( )。
(7)一个合数至少有( )个约数。
2
因数的个数
4
0
1
3
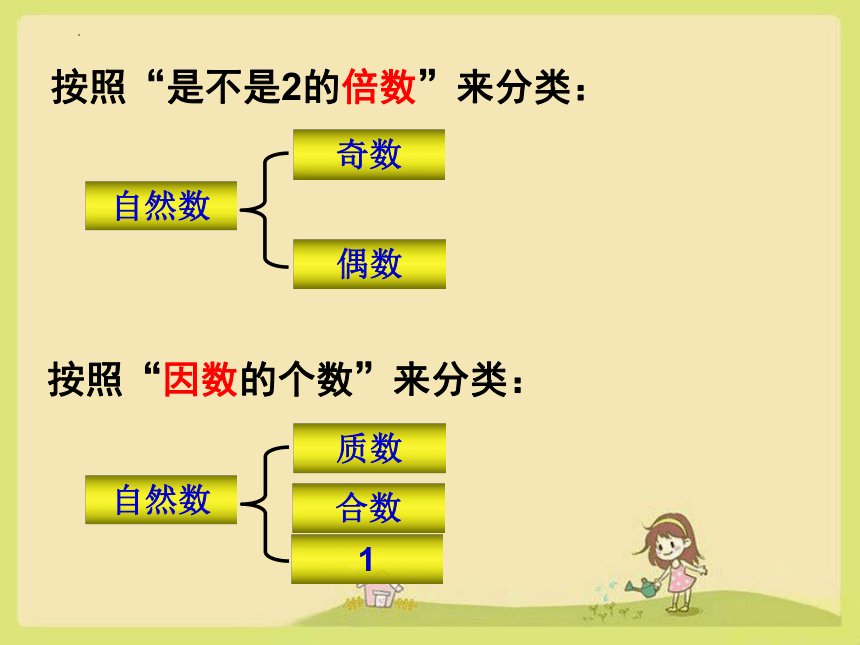
按照“因数的个数”来分类:
按照“是不是2的倍数”来分类:
自然数
奇数
偶数
自然数
质数
合数
1
自然数 偶数 奇数 质数 合数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
在整数1——20中:
奇数有 。
偶数有 。
质数有 。
合数有 。
1,3,5,7,9,11,13,15,17,19
2,4,6,8,10,12,14,16,18,20
2,3,5,7,11,13,17,19
4,6,8,9,10,12,14,15,16,18,20
判断
⑴一个自然数它不是奇数就是偶数。( )
⑵一个自然数它不是质数就是合数。( )
⑶质数都是奇数。 ( )
⑷合数都是偶数。 ( )
⑸质数有两个约数合数有三个约数。( )
⑹3的所有倍数都是合数。 ( )
⑺在自然数中,有无限多个质数,没
有最大的质数。 ( )
×
×
×
√
×
×
√
思 考:
1、是不是所有的质数都是奇数?
2、是不是所有的奇数都是质数?
3、是不是所有的合数都是偶数?
4、是不是所有的偶数都是合数?
2是质数,但不是奇数。
9、 15、 35等是奇数,但不是质数。
21、 49、 57等是合数,但不是偶数。
2是偶数,但不是合数。
猜一猜:看谁最快猜出陈老师家的电话号码?
第①位是10以内最大的质数。
第②位是10以内最小的合数。
第③位是10以内最大的既是偶数又是合数。
第④位这个数既不是质数也不是合数。
第⑤位是10以内最小的质数。
第⑥位是10以内最小的既是质数又是奇数。
第⑦位是10以内最大的既是奇数又是合数。
7481239
7
4
8
1
2
3
9
40=( )+( )
20= ( ) + ( )
18=( )+ ( )
28=( )+( )
你能把下列各数改写成两个质数和的形式吗?
23
17
3
17
训练
在( )里填适当的质数
6 =( )×( )
3
2
28 = ( )×( )× ( )
2
2
7
大家看:
6=2×3 28=2×2×7
其中:2,3,7 本身都是什么数?
小 结:
从上面的例子看出,每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,叫做这个合数的质因数。
把一个合数用质因数相乘的形式表示出来叫做分解质因数
质数
同时2,3,7 又都是合数的什么数?
因数
思考:因数与质因数有哪些联系和区别?
因数可能是质数,可能是合数,也可以既不是质数也
不是合数
质因数本身必须是质数,但它也是一个因数。
练一练:把30、12、18、48分解质因数。
30= 2 × 3 × 5
12= 2 × 2 × 3
18= 2 × 3 × 3
48= 2 × 2 × 2× 2 ×3
做一做: 下面各算式哪些是分解质因数,哪些不是 为什么
34=2 X 17 (2)36=4 X 9
(3)12=2 X 2 X 3 (4)15=3 X 5
(5)18=1 X2 X 3 X 3 (6)7 X 5=35
做一做: 下面各算式哪些是分解质因数,哪些不是 为什么
34=2 X 17 (2)36=4 X 9
(3)12=2 X 2 X 3 (4)15=3 X 5
(5)18=1 X2 X 3 X 3 (6)7 X 5=35
(1). (3).(4)是分解质因数.(2)式中4和9都不是36的质因数.(5)中含有1,1不是质数,也不当质因数.(6)式是一般的乘法算式,不是分解质因数.分解质因数要把合数写在等号的左边.
根据上面的方法请同学们自己动手把60分解质因数。
60
6
×
10
2
×
3
×
2
×
5
即: 60=2×3×2×5
注意: 分解质因数的书写格式是:
一定是一个合数分成几个质数相乘的形式。
填空:
35
( )
( )
×
45
3
×
( )
3
×
( )
( )
×
56
7
×
( )
7
×
( )
2
×
7
×
2
×
( )
( )
×
35= ————
45= ———————
56= ——————————
5×7
3×3×5
7×2×2×2
5
7
1 5
3
5
8
4
2
2
短除号
6
……被除数
2
除数……
3
……商
用短除法分解质因数
用短除法分解质因数的方法:
2 6
3
用质数2去除
商是质数为止
2 28
2 14
7
商是质数为止
商是合数还要继续除
2 60
2 30
3 15
5
合数继续除
合数继续除
商是质数为止
小 结
为了简便,通常用短除法来分解质因数。 例如:
2 6
3
2 28
14
2
7
2 60
30
2
15
3
5
6=2×3
28=2×2×7
把一个合数分解质因数,先用一个能整除这个合数的质数(通常从最小的开始)去除,得出的商如果是质数,就把除数和商写成相乘的形式;得出的商如果是合数,就照上面的方法继续除下去,直到得出的商是质数为止,然后把各个除数和最后的商写成连乘的形式。
60=2×2×3×5
考考你
1、用短除法把24 、 56分解质因数
24
2
12
6
2
2
3
56
2
2
2
28
14
7
24=2×2×2×3
56=2×2×2×7
2、判断题
(1)、6的因数有1、2、3、6,所以它们都是6的质因数。 ( )
(2)、整数都可以写成几个质数相乘的形式。 ( )
(3)、把24分解质因数是2 ×2 ×2 ×3=24 ( )
(4)、两个质数的乘积一定是一个合数。 ( )
考考你
√
×
×
×
考考你
3、选择题
(1)、2和5是20的( )
A:质数 B:质因数 C:约数
(2)、( )式是把30分解质因数。
A: 2×3×5=30 B: 30=5×6
C: 30=2×3×5
(3)、用短除法分解质因数时,除数要用( )
A:整数 B:约数 C:合数
D: 质数 E:用任何数
B,C
C
D
你能把下面各数分解质因数吗
0 12
16 72
3、看谁是个小判官.
⊙把35分解质因数是 35=1×5×7 ( )
×
×
⊙把49分解质因数是
7×7=49 ( )
⊙把30分解质因数是30=2×3×5 ( )
×
⊙51不能分解质因数.
( )
2、判断正误。对的画√,错的画×并找出错误的原因。
①2和5是质因数; ……………………( )
②一个合数的约数,就是它的质因数; ( )
③24分解质因数:24=1×2×2×2×3; ( )
④8分解质因数:8=2×2×2;…………( )
⑤30分解质因数:30=5×6; ……… ( )
⑥21分解质因数:3×7=21。 …………( )
⑦12分解质因数:12=2+3+7 …… ( )
质数和合数 复习
100以内质数表:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
填 空:
(1) 一个数除了( )和它的( ),不再有别的因数,这个数叫做( )数。
(2) 一个数除了( )和它的( ),还有别的因数,这个数叫做( )数。
(3) ( )不是质数,也不是合数。
(4)末尾是( )的整数是2的倍数: 末尾是( )的数是5的倍数,( )的数是3的倍数 。
1
本身
质
1
本身
合
1
0,2,4,6,8
0或5
各位上的数字的和能被3整除
(5)最小的质数是( ),最小的合数是( ),最小的偶数是( ),最小的奇数是( )。
(6)判断一个数是质数或合数的方法是根据( )。
(7)一个合数至少有( )个约数。
2
因数的个数
4
0
1
3
按照“因数的个数”来分类:
按照“是不是2的倍数”来分类:
自然数
奇数
偶数
自然数
质数
合数
1
自然数 偶数 奇数 质数 合数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
在整数1——20中:
奇数有 。
偶数有 。
质数有 。
合数有 。
1,3,5,7,9,11,13,15,17,19
2,4,6,8,10,12,14,16,18,20
2,3,5,7,11,13,17,19
4,6,8,9,10,12,14,15,16,18,20
判断
⑴一个自然数它不是奇数就是偶数。( )
⑵一个自然数它不是质数就是合数。( )
⑶质数都是奇数。 ( )
⑷合数都是偶数。 ( )
⑸质数有两个约数合数有三个约数。( )
⑹3的所有倍数都是合数。 ( )
⑺在自然数中,有无限多个质数,没
有最大的质数。 ( )
×
×
×
√
×
×
√
思 考:
1、是不是所有的质数都是奇数?
2、是不是所有的奇数都是质数?
3、是不是所有的合数都是偶数?
4、是不是所有的偶数都是合数?
2是质数,但不是奇数。
9、 15、 35等是奇数,但不是质数。
21、 49、 57等是合数,但不是偶数。
2是偶数,但不是合数。
猜一猜:看谁最快猜出陈老师家的电话号码?
第①位是10以内最大的质数。
第②位是10以内最小的合数。
第③位是10以内最大的既是偶数又是合数。
第④位这个数既不是质数也不是合数。
第⑤位是10以内最小的质数。
第⑥位是10以内最小的既是质数又是奇数。
第⑦位是10以内最大的既是奇数又是合数。
7481239
7
4
8
1
2
3
9
40=( )+( )
20= ( ) + ( )
18=( )+ ( )
28=( )+( )
你能把下列各数改写成两个质数和的形式吗?
23
17
3
17
训练
在( )里填适当的质数
6 =( )×( )
3
2
28 = ( )×( )× ( )
2
2
7
大家看:
6=2×3 28=2×2×7
其中:2,3,7 本身都是什么数?
小 结:
从上面的例子看出,每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,叫做这个合数的质因数。
把一个合数用质因数相乘的形式表示出来叫做分解质因数
质数
同时2,3,7 又都是合数的什么数?
因数
思考:因数与质因数有哪些联系和区别?
因数可能是质数,可能是合数,也可以既不是质数也
不是合数
质因数本身必须是质数,但它也是一个因数。
练一练:把30、12、18、48分解质因数。
30= 2 × 3 × 5
12= 2 × 2 × 3
18= 2 × 3 × 3
48= 2 × 2 × 2× 2 ×3
做一做: 下面各算式哪些是分解质因数,哪些不是 为什么
34=2 X 17 (2)36=4 X 9
(3)12=2 X 2 X 3 (4)15=3 X 5
(5)18=1 X2 X 3 X 3 (6)7 X 5=35
做一做: 下面各算式哪些是分解质因数,哪些不是 为什么
34=2 X 17 (2)36=4 X 9
(3)12=2 X 2 X 3 (4)15=3 X 5
(5)18=1 X2 X 3 X 3 (6)7 X 5=35
(1). (3).(4)是分解质因数.(2)式中4和9都不是36的质因数.(5)中含有1,1不是质数,也不当质因数.(6)式是一般的乘法算式,不是分解质因数.分解质因数要把合数写在等号的左边.
根据上面的方法请同学们自己动手把60分解质因数。
60
6
×
10
2
×
3
×
2
×
5
即: 60=2×3×2×5
注意: 分解质因数的书写格式是:
一定是一个合数分成几个质数相乘的形式。
填空:
35
( )
( )
×
45
3
×
( )
3
×
( )
( )
×
56
7
×
( )
7
×
( )
2
×
7
×
2
×
( )
( )
×
35= ————
45= ———————
56= ——————————
5×7
3×3×5
7×2×2×2
5
7
1 5
3
5
8
4
2
2
短除号
6
……被除数
2
除数……
3
……商
用短除法分解质因数
用短除法分解质因数的方法:
2 6
3
用质数2去除
商是质数为止
2 28
2 14
7
商是质数为止
商是合数还要继续除
2 60
2 30
3 15
5
合数继续除
合数继续除
商是质数为止
小 结
为了简便,通常用短除法来分解质因数。 例如:
2 6
3
2 28
14
2
7
2 60
30
2
15
3
5
6=2×3
28=2×2×7
把一个合数分解质因数,先用一个能整除这个合数的质数(通常从最小的开始)去除,得出的商如果是质数,就把除数和商写成相乘的形式;得出的商如果是合数,就照上面的方法继续除下去,直到得出的商是质数为止,然后把各个除数和最后的商写成连乘的形式。
60=2×2×3×5
考考你
1、用短除法把24 、 56分解质因数
24
2
12
6
2
2
3
56
2
2
2
28
14
7
24=2×2×2×3
56=2×2×2×7
2、判断题
(1)、6的因数有1、2、3、6,所以它们都是6的质因数。 ( )
(2)、整数都可以写成几个质数相乘的形式。 ( )
(3)、把24分解质因数是2 ×2 ×2 ×3=24 ( )
(4)、两个质数的乘积一定是一个合数。 ( )
考考你
√
×
×
×
考考你
3、选择题
(1)、2和5是20的( )
A:质数 B:质因数 C:约数
(2)、( )式是把30分解质因数。
A: 2×3×5=30 B: 30=5×6
C: 30=2×3×5
(3)、用短除法分解质因数时,除数要用( )
A:整数 B:约数 C:合数
D: 质数 E:用任何数
B,C
C
D
你能把下面各数分解质因数吗
0 12
16 72
3、看谁是个小判官.
⊙把35分解质因数是 35=1×5×7 ( )
×
×
⊙把49分解质因数是
7×7=49 ( )
⊙把30分解质因数是30=2×3×5 ( )
×
⊙51不能分解质因数.
( )
2、判断正误。对的画√,错的画×并找出错误的原因。
①2和5是质因数; ……………………( )
②一个合数的约数,就是它的质因数; ( )
③24分解质因数:24=1×2×2×2×3; ( )
④8分解质因数:8=2×2×2;…………( )
⑤30分解质因数:30=5×6; ……… ( )
⑥21分解质因数:3×7=21。 …………( )
⑦12分解质因数:12=2+3+7 …… ( )
