2024海南中考数学二轮重点专题研究 微专题 二次函数与面积问题课件(36张PPT)
文档属性
| 名称 | 2024海南中考数学二轮重点专题研究 微专题 二次函数与面积问题课件(36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 10:23:45 | ||
图片预览






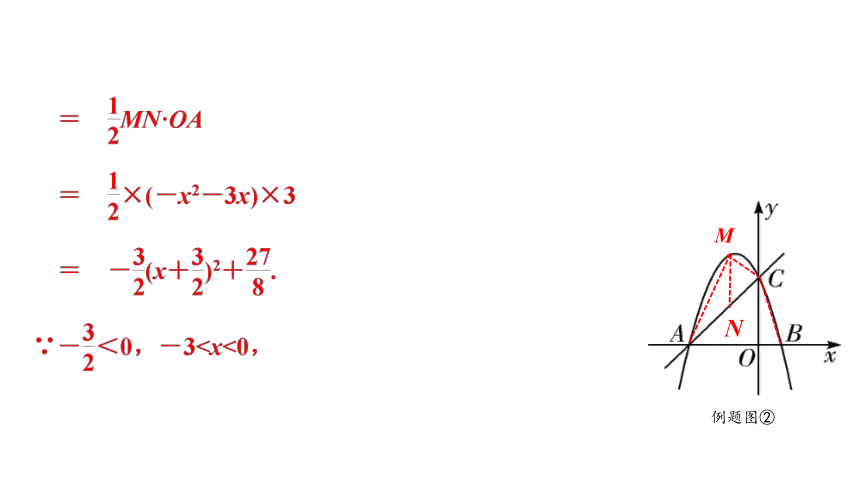




文档简介
(共36张PPT)
【思维教练】由抛物线解析式可以得出点C的坐标,根据点P的横坐标为2及三角形的面积公式即可求解.
例题图①
【思维教练】△ABC面积为定值,当四边形MABC的面积最大,即△MAC的面积最大,将△MAC的面积用含字母的式子表示出来,再利用二次函数性质讨论其最值,进而求出点M的坐标.
解:存在;
如解图,过点M作MN∥y轴,交AC于点N,连接MA,MC,BC,
例题图②
M
N
例题图②
M
N
例题图②
M
N
例题图②
M
N
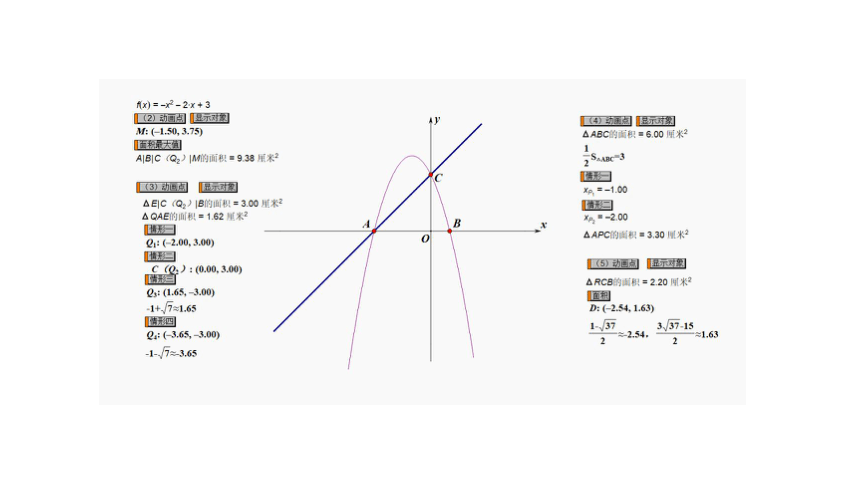
【思维教练】因为△QAE和△CBE的底边AE=BE,所以只需高相等即可得面积相等.
例题解图②
例题解图②
【思维教练】△ABC的面积为定值,△PAC的面积可以用含字母的式子表示出来,根据两个三角形面积关系列等式求解即可.
例题图④
例题图④
F
N
【解法提示】如解图,过点P作PF⊥x轴于点F,交AC于点N,
设点P的坐标为(t,-t2-2t+3)(-3例题图④
F
N
例题图⑤
【思维教练】假设点R存在,过点R作BC的垂线交BC于点K,则
BC·RK= ,由于点R,K的坐标不易求得,可考虑作RH∥y轴交BC的延长线于点F,利用△RKF∽△BOC的性质,列等量关系式求解即可.
例题图⑥
例题图⑥
第1题图
解:存在,
如解图,连接BC,AC,
∴直线BC的解析式为y=2x+8,
∵点A与B关于抛物线对称轴对称,
直线BC与抛物线对称轴x=-1的交点为Q,
连接AQ,此时△QAC的周长最小.
第1题图
Q
第2题图
第2题图
第2题图
第2题图
【思维教练】由抛物线解析式可以得出点C的坐标,根据点P的横坐标为2及三角形的面积公式即可求解.
例题图①
【思维教练】△ABC面积为定值,当四边形MABC的面积最大,即△MAC的面积最大,将△MAC的面积用含字母的式子表示出来,再利用二次函数性质讨论其最值,进而求出点M的坐标.
解:存在;
如解图,过点M作MN∥y轴,交AC于点N,连接MA,MC,BC,
例题图②
M
N
例题图②
M
N
例题图②
M
N
例题图②
M
N
【思维教练】因为△QAE和△CBE的底边AE=BE,所以只需高相等即可得面积相等.
例题解图②
例题解图②
【思维教练】△ABC的面积为定值,△PAC的面积可以用含字母的式子表示出来,根据两个三角形面积关系列等式求解即可.
例题图④
例题图④
F
N
【解法提示】如解图,过点P作PF⊥x轴于点F,交AC于点N,
设点P的坐标为(t,-t2-2t+3)(-3
F
N
例题图⑤
【思维教练】假设点R存在,过点R作BC的垂线交BC于点K,则
BC·RK= ,由于点R,K的坐标不易求得,可考虑作RH∥y轴交BC的延长线于点F,利用△RKF∽△BOC的性质,列等量关系式求解即可.
例题图⑥
例题图⑥
第1题图
解:存在,
如解图,连接BC,AC,
∴直线BC的解析式为y=2x+8,
∵点A与B关于抛物线对称轴对称,
直线BC与抛物线对称轴x=-1的交点为Q,
连接AQ,此时△QAC的周长最小.
第1题图
Q
第2题图
第2题图
第2题图
第2题图
同课章节目录
