西师大版四年级下册数学乘法运算律及简便运算 课件(共23张PPT)
文档属性
| 名称 | 西师大版四年级下册数学乘法运算律及简便运算 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 22:15:13 | ||
图片预览






文档简介
(共23张PPT)
交换律
结合律
加法
加法
利用加法运算律填空
45+56=56+
甲数+乙数=乙数+
25+49+51=25 +( + )
10+ B +C= +( + )
45
49
51
甲数
10
B
C
加法交换律:两个数相加,交换加数的位置,和不变。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
交换律
结合律
乘法 ?
乘法 ?
第二单元 乘除法的关系和乘法运算律
第三课时 乘法交换律和乘法结合律
预学指导
计算下面各题:
4×20= 25×5×4=
20×4= 25×(5×4)=
(1)观察上下两个算式,你有什么发现?
(2)你能用自己的话说一说上下两个算式之间的关系吗?
(3)试一试:你还能写出这样的算式吗?
80
80
500
500
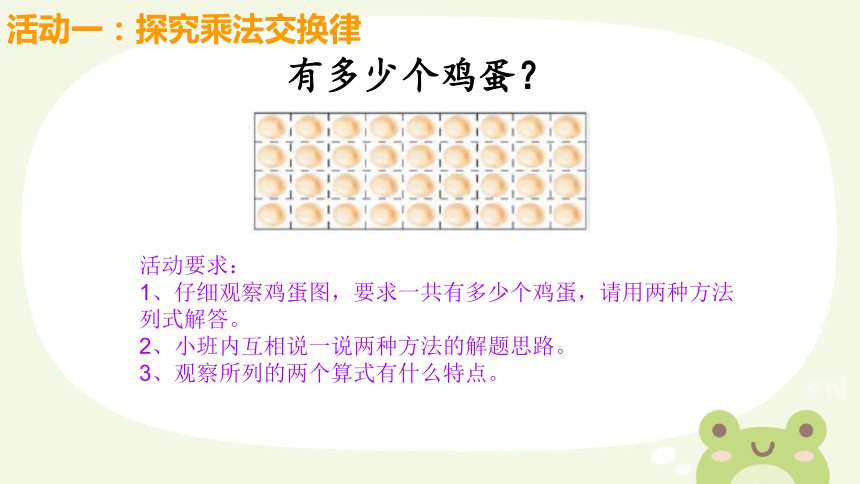
活动一:探究乘法交换律
有多少个鸡蛋?
活动要求:
1、仔细观察鸡蛋图,要求一共有多少个鸡蛋,请用两种方法列式解答。
2、小班内互相说一说两种方法的解题思路。
3、观察所列的两个算式有什么特点。
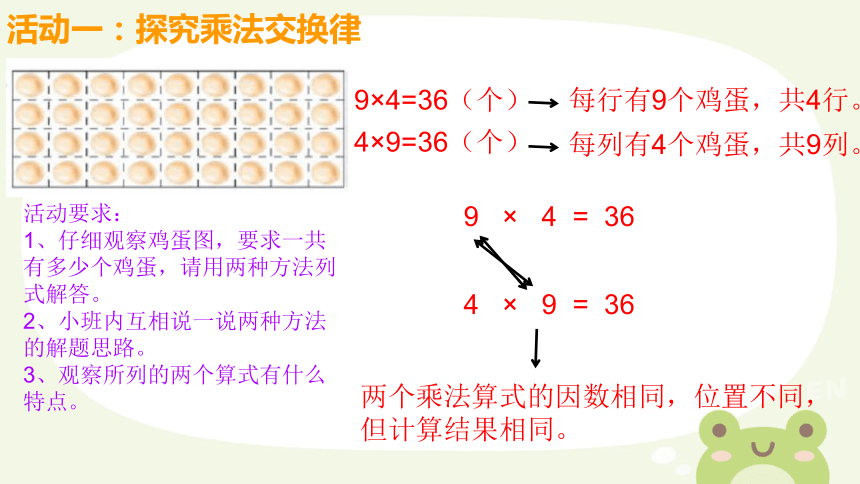
活动一:探究乘法交换律
活动要求:
1、仔细观察鸡蛋图,要求一共有多少个鸡蛋,请用两种方法列式解答。
2、小班内互相说一说两种方法的解题思路。
3、观察所列的两个算式有什么特点。
9×4=36(个)
4×9=36(个)
每行有9个鸡蛋,共4行。
每列有4个鸡蛋,共9列。
9 × 4 = 36
4 × 9 = 36
两个乘法算式的因数相同,位置不同,但计算结果相同。
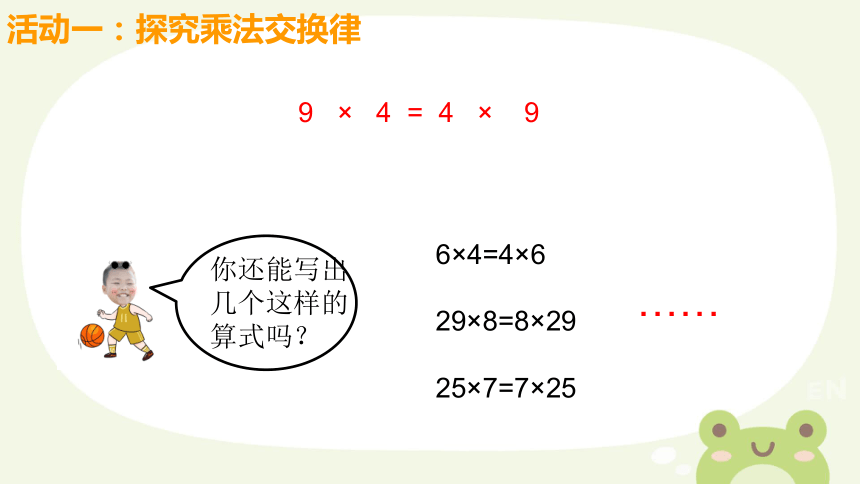
9 × 4 = 4 × 9
活动一:探究乘法交换律
你还能写出几个这样的算式吗?
6×4=4×6
29×8=8×29
25×7=7×25
……
活动一:探究乘法交换律
6×4=4×6 29×8=8×29 25×7=7×25
根据加法交换律,你能总结出它们的规律吗?
两个数相乘,交换因数的位置,积不变,这就是乘法交换律。
用文字表示
用符号表示
☆×□=□×☆
用字母表示
a×b=b×a
用字母表示 a×b=b×a
根据乘法交换律,将下面的算式补充完整。
15 × 11 × 6 = 15 ×( )×11
6
75 × 7 × 2 = 75 × ( )× 7
25 × 6 = 2 ×( )×3
△ × □ = □ ×( )
A × B × C = B ×( )× C
2
25
△
A
多个数相乘,任意交换因数的位置,积不变
活动二:探究乘法结合律
这个小区一共有多少户?
活动要求:
1、说一说:这道题的已知条件和问题分别是什么?
2、要求这个小区共有多少户,试一试你能列出综合算式解决吗?
3、根据自己所列的算式在小班内交流,先算的什么,再算的什么。
4、认真观察这两个算式的数据和结果,你有什么发现?
活动二:探究乘法结合律
这个小区一共有多少户?
每层6户
×
每幢24层
每幢楼的户数
×
8幢楼
这个小区共有的户数
6×24×8
=144×8
=1152(户)
答:这个小区一共有1152户。
活动二:探究乘法结合律
这个小区一共有多少户?
每层6户
×
每幢24层
8幢楼共有的层数
×
8幢楼
这个小区共有的户数
6×(24×8)
=6×192
=1152(户)
答:这个小区一共有1152户。
活动二:探究乘法结合律
6 × 24 × 8
6 × ( 24 × 8)
先把前两个数相乘,再乘第三个数
先把后两个数相乘,再乘第一个数
结果相同
6 ×24×8=6×(24×8)
活动二:探究乘法结合律
16×5×2= 35×25×4= 12× (125×8)= 16× (5×2)= 35× (25×4)= 12×125×8=
仔细观察这三组算式,每组上下两个算式有什么相同点和不同点?
160
160
3500
3500
12000
12000
举例验证
活动二:探究乘法结合律
得出结论
总结方法
从实例中找出相等的两道算式
观察特征
提出猜想
举例验证
得出结论
拓展练习
说说下面的算式运用了什么运算定律。
34 × 33 = 33 × 34
乘法交换律
(60×25)×8 =60×(25×8)
乘法结合律
125×5×8= 5 ×(125×8)
乘法交换律
乘法结合律
这节课你有哪些收获?
你认为哪些同学表现最好呢?
课后作业
1、课后跟你的同桌一起完成数学书13页课堂活动第一题。
2、练习四第1、2题。
3、思考:乘法运算律能否给乘法运算带来简便呢?
交换律
结合律
加法
加法
利用加法运算律填空
45+56=56+
甲数+乙数=乙数+
25+49+51=25 +( + )
10+ B +C= +( + )
45
49
51
甲数
10
B
C
加法交换律:两个数相加,交换加数的位置,和不变。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
交换律
结合律
乘法 ?
乘法 ?
第二单元 乘除法的关系和乘法运算律
第三课时 乘法交换律和乘法结合律
预学指导
计算下面各题:
4×20= 25×5×4=
20×4= 25×(5×4)=
(1)观察上下两个算式,你有什么发现?
(2)你能用自己的话说一说上下两个算式之间的关系吗?
(3)试一试:你还能写出这样的算式吗?
80
80
500
500
活动一:探究乘法交换律
有多少个鸡蛋?
活动要求:
1、仔细观察鸡蛋图,要求一共有多少个鸡蛋,请用两种方法列式解答。
2、小班内互相说一说两种方法的解题思路。
3、观察所列的两个算式有什么特点。
活动一:探究乘法交换律
活动要求:
1、仔细观察鸡蛋图,要求一共有多少个鸡蛋,请用两种方法列式解答。
2、小班内互相说一说两种方法的解题思路。
3、观察所列的两个算式有什么特点。
9×4=36(个)
4×9=36(个)
每行有9个鸡蛋,共4行。
每列有4个鸡蛋,共9列。
9 × 4 = 36
4 × 9 = 36
两个乘法算式的因数相同,位置不同,但计算结果相同。
9 × 4 = 4 × 9
活动一:探究乘法交换律
你还能写出几个这样的算式吗?
6×4=4×6
29×8=8×29
25×7=7×25
……
活动一:探究乘法交换律
6×4=4×6 29×8=8×29 25×7=7×25
根据加法交换律,你能总结出它们的规律吗?
两个数相乘,交换因数的位置,积不变,这就是乘法交换律。
用文字表示
用符号表示
☆×□=□×☆
用字母表示
a×b=b×a
用字母表示 a×b=b×a
根据乘法交换律,将下面的算式补充完整。
15 × 11 × 6 = 15 ×( )×11
6
75 × 7 × 2 = 75 × ( )× 7
25 × 6 = 2 ×( )×3
△ × □ = □ ×( )
A × B × C = B ×( )× C
2
25
△
A
多个数相乘,任意交换因数的位置,积不变
活动二:探究乘法结合律
这个小区一共有多少户?
活动要求:
1、说一说:这道题的已知条件和问题分别是什么?
2、要求这个小区共有多少户,试一试你能列出综合算式解决吗?
3、根据自己所列的算式在小班内交流,先算的什么,再算的什么。
4、认真观察这两个算式的数据和结果,你有什么发现?
活动二:探究乘法结合律
这个小区一共有多少户?
每层6户
×
每幢24层
每幢楼的户数
×
8幢楼
这个小区共有的户数
6×24×8
=144×8
=1152(户)
答:这个小区一共有1152户。
活动二:探究乘法结合律
这个小区一共有多少户?
每层6户
×
每幢24层
8幢楼共有的层数
×
8幢楼
这个小区共有的户数
6×(24×8)
=6×192
=1152(户)
答:这个小区一共有1152户。
活动二:探究乘法结合律
6 × 24 × 8
6 × ( 24 × 8)
先把前两个数相乘,再乘第三个数
先把后两个数相乘,再乘第一个数
结果相同
6 ×24×8=6×(24×8)
活动二:探究乘法结合律
16×5×2= 35×25×4= 12× (125×8)= 16× (5×2)= 35× (25×4)= 12×125×8=
仔细观察这三组算式,每组上下两个算式有什么相同点和不同点?
160
160
3500
3500
12000
12000
举例验证
活动二:探究乘法结合律
得出结论
总结方法
从实例中找出相等的两道算式
观察特征
提出猜想
举例验证
得出结论
拓展练习
说说下面的算式运用了什么运算定律。
34 × 33 = 33 × 34
乘法交换律
(60×25)×8 =60×(25×8)
乘法结合律
125×5×8= 5 ×(125×8)
乘法交换律
乘法结合律
这节课你有哪些收获?
你认为哪些同学表现最好呢?
课后作业
1、课后跟你的同桌一起完成数学书13页课堂活动第一题。
2、练习四第1、2题。
3、思考:乘法运算律能否给乘法运算带来简便呢?
