与矩形有关的折叠问题教案
图片预览
文档简介
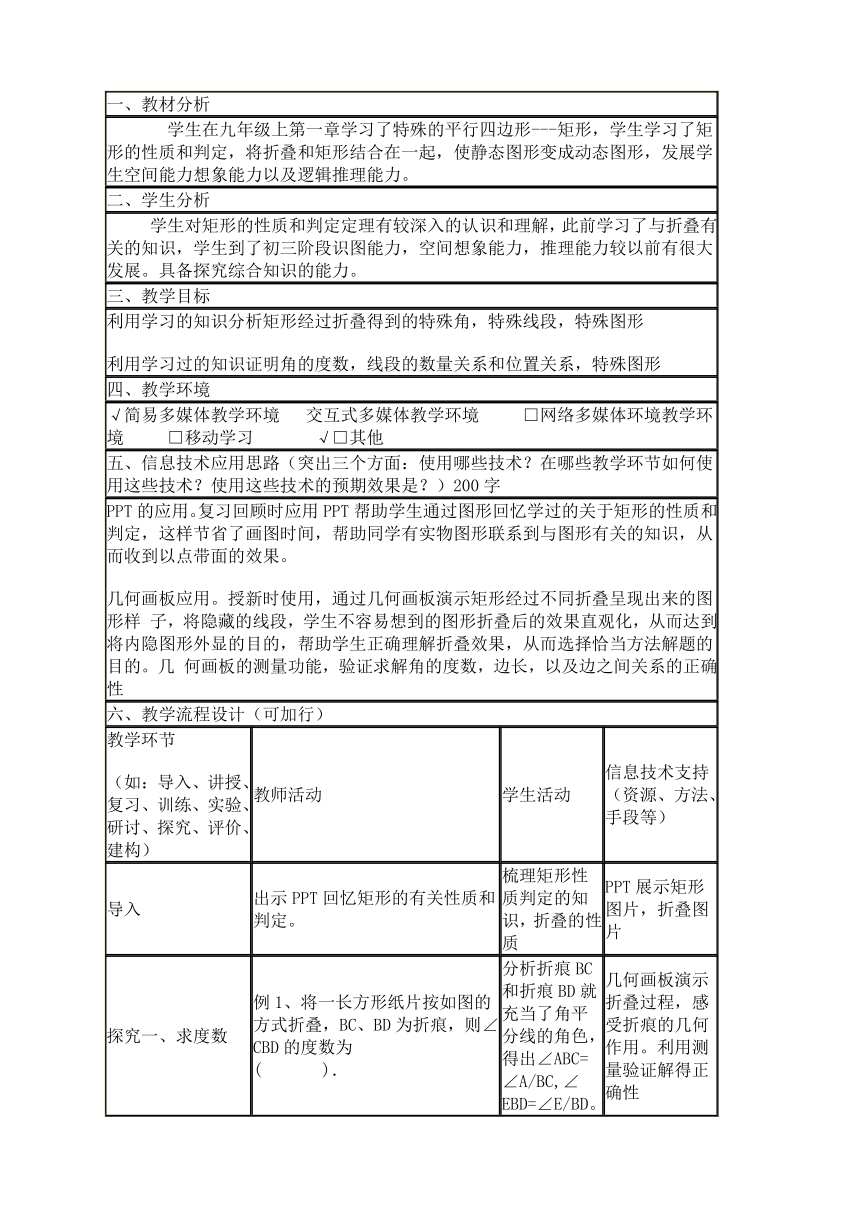
一、教材分析
学生在九年级上第一章学习了特殊的 ( http: / / www.21cnjy.com )平行四边形---矩形,学生学习了矩形的性质和判定,将折叠和矩形结合在一起,使静态图形变成动态图形,发展学生空间能力想象能力以及逻辑推理能力。
二、学生分析
学生对矩形的性质和判定定理有较深入的 ( http: / / www.21cnjy.com )认识和理解,此前学习了与折叠有关的知识,学生到了初三阶段识图能力,空间想象能力,推理能力较以前有很大发展。具备探究综合知识的能力。
三、教学目标
利用学习的知识分析矩形经过折叠得到的特殊角,特殊线段,特殊图形 利用学习过的知识证明角的度数,线段的数量关系和位置关系,特殊图形
四、教学环境
√简易多媒体教学环境 交互式多媒体教学环境 □网络多媒体环境教学环境 □移动学习 √□其他
五、信息技术应用思路(突出三个方面:使用哪些技术?在哪些教学环节如何使用这些技术?使用这些技术的预期效果是?)200字
PPT的应用。复习回顾时应 ( http: / / www.21cnjy.com )用PPT帮助学生 ( http: / / www.21cnjy.com )通过图形回忆学过的关于矩形的性质和判定,这样节省了画图时间,帮助同学有实物图形联系到与图形有关的知识,从而收到以点带面的效果。 几何画板应用。授新时使用,通过几何画板演示矩形经过不同折叠呈现出来的图形样 子,将隐藏的线段,学生不容易想到的图形折叠后的效果直观化,从而达到将内隐图形外显的目的,帮助学生正确理解折叠效果,从而选择恰当方法解题的目的。几 何画板的测量功能,验证求解角的度数,边长,以及边之间关系的正确性
六、教学流程设计(可加行)
教学环节 (如:导入、讲授、复习、训练、实验、研讨、探究、评价、建构) 教师活动 学生活动 信息技术支持(资源、方法、手段等)
导入 出示PPT回忆矩形的有关性质和判定。 梳理矩形性质判定的知识,折叠的性质 PPT展示矩形图片,折叠图片
探究一、求度数 例1、将一长方形纸片按如图的方式折叠,BC、BD为折痕,则∠CBD的度数为( ). 分析折痕BC和折痕BD就充当了角平分线 ( http: / / www.21cnjy.com )的角色,得出∠ABC=∠A/BC,∠EBD=∠E/BD。指导学生利用几何画板的测量功能验证求解结果。 几何画板演示折叠过程,感受折痕的几何作用。利用测量验证解得正确性
探究二求线段的数量关系和位置关系
例2、如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O。 (1)由折叠可得△BCD≌△BED,除此之外,图中还存在其他的全等三角形,请你找出来 。 (2)图中有等腰三角形吗?请你找出来 。 (3)若AB=6,BC=8,则O点到BD的距离是 。 动手折一折,画一画,找出线段间的数量和位置关系,测量线段长度,度量点到直线的距离长度来验证自己的逻辑证明或求解的正确性。 几何画板演示,探究线段关系
探究三求点的坐标 例3、已知:如图,矩形AOBC,以 ( http: / / www.21cnjy.com )O为坐标原点,OB,OA分别在x轴、y轴上,点A坐标为(0,3),∠OAB=60°,以AB为轴对折后,使C点落在D点处,求D点的坐标. 分析矩形放置在平面直角坐标系的背景下,点的坐标。通过几何画板操作给出平面直角坐标系,直观结果和求解结果相对比,验证求解的点的坐标的正确性 几何画板演示
探究四 例4、一个矩形纸片如图折叠,使顶点B和D重合,折痕为EF。 (1)找出图中全等的三角形,并证明。 (2)重合部分是什么图形?证明你的结论。 (3)连接BE,并判断四边形BEDF是什么特殊四边形,BD与EF有什么关系?并证明。 学生分析图形找出已知条件和要证明结 ( http: / / www.21cnjy.com )论的关系。多条路径展现求解过程。归纳总结矩形折叠的规律利用几何画板的测量功能证明四边形的边之间的关系,从而为证明特殊四边形找到直观证据。 几何画板展示
练习 例5、在矩形ABDC中,把∠A沿CF折叠,点A恰好落在矩形的对称中心E处,若AB=a,AC=b,请你计算 b/a 的值。 经过前面例题学习,感悟矩形折叠会出现的几种类型问题,学会分类思考。 多媒体展示,电子白板功能,学生画一画。
学生在九年级上第一章学习了特殊的 ( http: / / www.21cnjy.com )平行四边形---矩形,学生学习了矩形的性质和判定,将折叠和矩形结合在一起,使静态图形变成动态图形,发展学生空间能力想象能力以及逻辑推理能力。
二、学生分析
学生对矩形的性质和判定定理有较深入的 ( http: / / www.21cnjy.com )认识和理解,此前学习了与折叠有关的知识,学生到了初三阶段识图能力,空间想象能力,推理能力较以前有很大发展。具备探究综合知识的能力。
三、教学目标
利用学习的知识分析矩形经过折叠得到的特殊角,特殊线段,特殊图形 利用学习过的知识证明角的度数,线段的数量关系和位置关系,特殊图形
四、教学环境
√简易多媒体教学环境 交互式多媒体教学环境 □网络多媒体环境教学环境 □移动学习 √□其他
五、信息技术应用思路(突出三个方面:使用哪些技术?在哪些教学环节如何使用这些技术?使用这些技术的预期效果是?)200字
PPT的应用。复习回顾时应 ( http: / / www.21cnjy.com )用PPT帮助学生 ( http: / / www.21cnjy.com )通过图形回忆学过的关于矩形的性质和判定,这样节省了画图时间,帮助同学有实物图形联系到与图形有关的知识,从而收到以点带面的效果。 几何画板应用。授新时使用,通过几何画板演示矩形经过不同折叠呈现出来的图形样 子,将隐藏的线段,学生不容易想到的图形折叠后的效果直观化,从而达到将内隐图形外显的目的,帮助学生正确理解折叠效果,从而选择恰当方法解题的目的。几 何画板的测量功能,验证求解角的度数,边长,以及边之间关系的正确性
六、教学流程设计(可加行)
教学环节 (如:导入、讲授、复习、训练、实验、研讨、探究、评价、建构) 教师活动 学生活动 信息技术支持(资源、方法、手段等)
导入 出示PPT回忆矩形的有关性质和判定。 梳理矩形性质判定的知识,折叠的性质 PPT展示矩形图片,折叠图片
探究一、求度数 例1、将一长方形纸片按如图的方式折叠,BC、BD为折痕,则∠CBD的度数为( ). 分析折痕BC和折痕BD就充当了角平分线 ( http: / / www.21cnjy.com )的角色,得出∠ABC=∠A/BC,∠EBD=∠E/BD。指导学生利用几何画板的测量功能验证求解结果。 几何画板演示折叠过程,感受折痕的几何作用。利用测量验证解得正确性
探究二求线段的数量关系和位置关系
例2、如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O。 (1)由折叠可得△BCD≌△BED,除此之外,图中还存在其他的全等三角形,请你找出来 。 (2)图中有等腰三角形吗?请你找出来 。 (3)若AB=6,BC=8,则O点到BD的距离是 。 动手折一折,画一画,找出线段间的数量和位置关系,测量线段长度,度量点到直线的距离长度来验证自己的逻辑证明或求解的正确性。 几何画板演示,探究线段关系
探究三求点的坐标 例3、已知:如图,矩形AOBC,以 ( http: / / www.21cnjy.com )O为坐标原点,OB,OA分别在x轴、y轴上,点A坐标为(0,3),∠OAB=60°,以AB为轴对折后,使C点落在D点处,求D点的坐标. 分析矩形放置在平面直角坐标系的背景下,点的坐标。通过几何画板操作给出平面直角坐标系,直观结果和求解结果相对比,验证求解的点的坐标的正确性 几何画板演示
探究四 例4、一个矩形纸片如图折叠,使顶点B和D重合,折痕为EF。 (1)找出图中全等的三角形,并证明。 (2)重合部分是什么图形?证明你的结论。 (3)连接BE,并判断四边形BEDF是什么特殊四边形,BD与EF有什么关系?并证明。 学生分析图形找出已知条件和要证明结 ( http: / / www.21cnjy.com )论的关系。多条路径展现求解过程。归纳总结矩形折叠的规律利用几何画板的测量功能证明四边形的边之间的关系,从而为证明特殊四边形找到直观证据。 几何画板展示
练习 例5、在矩形ABDC中,把∠A沿CF折叠,点A恰好落在矩形的对称中心E处,若AB=a,AC=b,请你计算 b/a 的值。 经过前面例题学习,感悟矩形折叠会出现的几种类型问题,学会分类思考。 多媒体展示,电子白板功能,学生画一画。
