1.1 直角三角形的性质和判定(I)第1课时 课件(共23张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 1.1 直角三角形的性质和判定(I)第1课时 课件(共23张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 452.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
第1章 直角三角形
1.1 直角三角形的性质和判定(I)
第1课时 直角三角形的性质和判定
学习目标
1.了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余;直角三角形斜边上的中线等于斜边的一半.
2.掌握有两个角互余的三角形是直角三角形.
学习重点、难点
直角三角形的性质定理(直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半).
会判定一个三角形是直角三角形.
重点:
难点:
性质定理“直角三角形斜边上的中线等于斜边的一半”的探索推导过程.
知识回顾
我们已经学习了三角形边与边,边与角,角与角之间的一些性质,你能列举出一些吗?
直角三角形作为一种特殊的三角形,除了具有一般三角形的性质外,它还具有哪些特殊性质呢?
如:三角形内角和为180°……
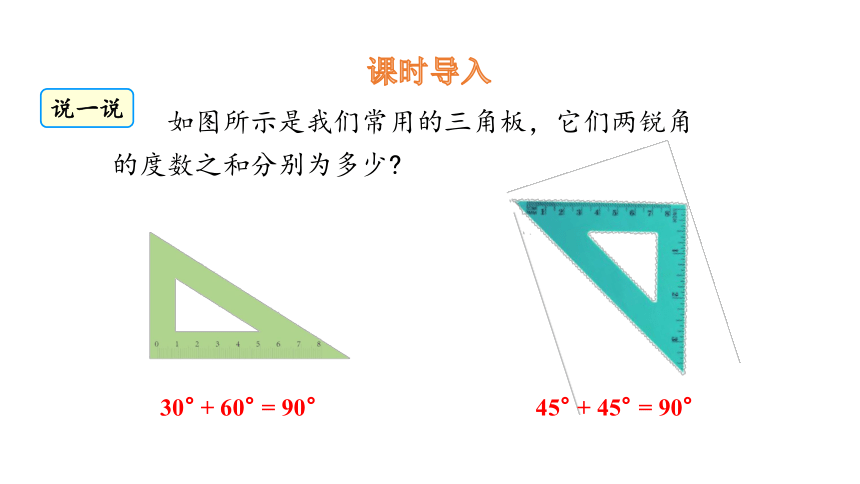
课时导入
如图所示是我们常用的三角板,它们两锐角的度数之和分别为多少
说一说
30° + 60° = 90°
45° + 45° = 90°
如图,在 Rt△ABC 中,∠C = 90°,两锐角的和等于多少呢?
在 Rt△ABC 中,由三角形内角和定理,得∠A +∠B +∠C = 180°,因为 ∠C = 90°,故∠A + ∠B = 90°.
思考:由此,你可以得到直角三角形有什么性质呢?
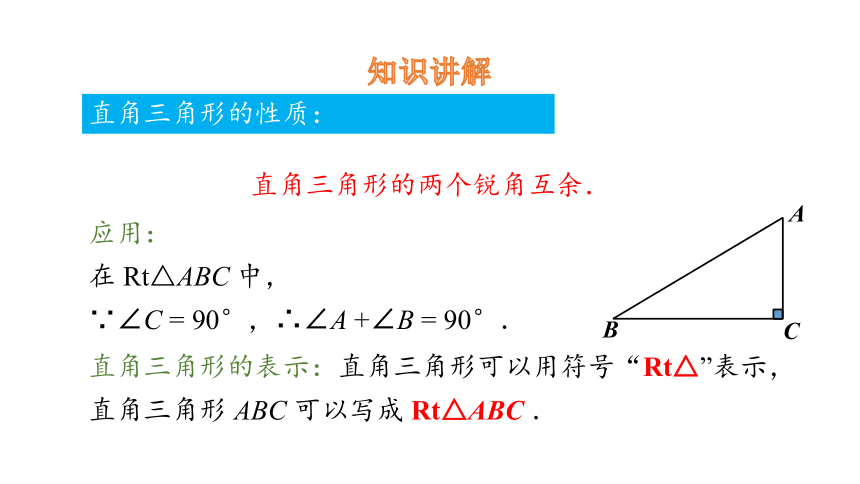
知识讲解
直角三角形的性质:
直角三角形的两个锐角互余.
应用:
在 Rt△ABC 中,
∵∠C = 90°,∴∠A +∠B = 90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形 ABC 可以写成 Rt△ABC .
A
B
C
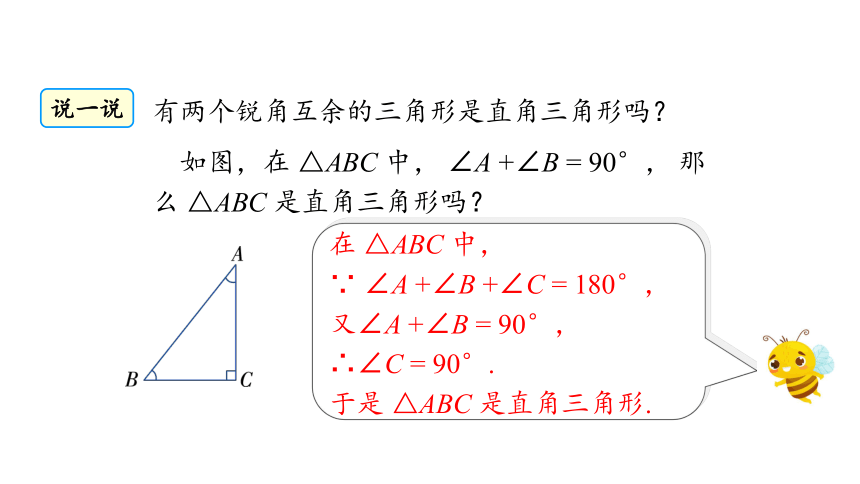
如图,在 △ABC 中, ∠A +∠B = 90°, 那么 △ABC 是直角三角形吗?
有两个锐角互余的三角形是直角三角形吗?
在 △ABC 中,
∵ ∠A +∠B +∠C = 180°, 又∠A +∠B = 90°,
∴∠C = 90°.
于是 △ABC 是直角三角形.
说一说
知识讲解
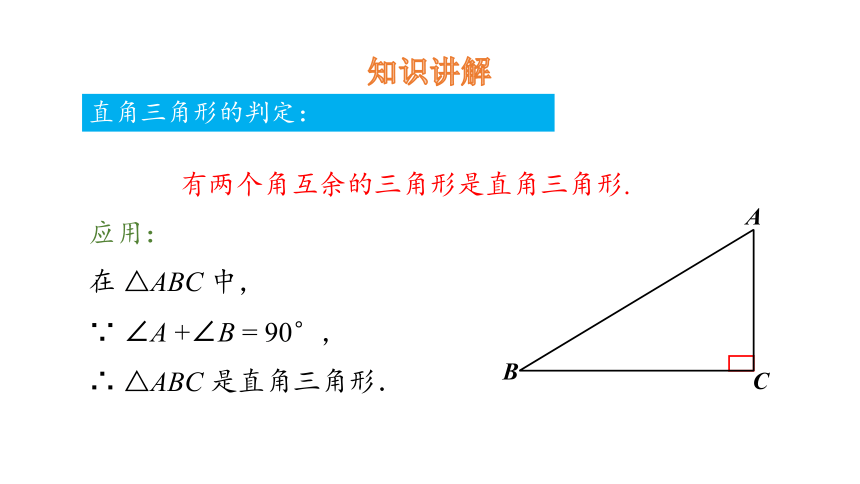
直角三角形的判定:
有两个角互余的三角形是直角三角形.
应用:
在 △ABC 中,
∵ ∠A +∠B = 90°,
∴ △ABC 是直角三角形.
A
B
C
探究
如图,画一个 Rt△ABC, 并作出斜边 AB 上的中线 CD,比较线段 CD 与线段 AB 之间长度,你能得出什么结论?
我测量后发现
CD = AB.
线段 CD 比线段 AB 短.
猜想:直角三角形斜边上的中线等于斜边的一半.
试给出数学证明.
图1-4
如图 1-3, 如果中线 CD = AB,则有∠DCA = ∠A .
由此受到启发,在图 1-4 的 Rt△ABC 中,过直角顶点 C 作射线 CD′ 交 AB 于 D′,使∠D′CA = ∠A ,则 CD′ = AD′ .
图1-3
证一证
∴ 点 D' 是斜边上的中点,即 CD' 是斜边 AB 的中线.
又∵∠A +∠B = 90°,∠D′CA +∠D′CB = 90°,
∴ ∠B = ∠D′CB.
∴CD′ = BD′.
故得
从而 CD 与 CD' 重合,由此得到:
性质:直角三角形斜边上的中线等于斜边的一半.
例
如图,已知 CD 是 △ABC 的 AB 边上的中线,且 . 求证:△ABC 是直角三角形.
证明:
∴ ∠1 = ∠A,∠2 = ∠B .
∵∠A +∠B +∠ACB = 180°,∠ACB = ∠1 + ∠2,
∴∠A +∠B +∠1 +∠2 = 180°,
∴ 2(∠A +∠B) = 180°.
∴ ∠A +∠B = 90°.
∴ △ABC 是直角三角形.
随 堂 小 测
1. 在一个直角三角形中,有一个锐角等于 40°,则另一个锐角的度数是( )
A.40° B.50°
C.60° D.70°
B
2. 具备下列条件的 △ABC 中,不是直角三角形的是( )
A.∠A + ∠B = ∠C
B.∠A - ∠B = ∠C
C.∠A∶∠B∶∠C = 1∶2∶3
D.∠A = ∠B = 3∠C
D
3. 如图所示,△ABC 为直角三角形,∠ACB = 90°,
CD⊥AB,与 ∠1 互余的角有( )
A.∠B
B.∠A
C.∠BCD 和 ∠A
D.∠BCD
C
4. 如图,在 △ABC 中,∠ABC = 90°,BD 是斜边 AC 上的中线.
(1)若 BD = 3 cm,则 AC =_____cm;
(2)若∠C = 30°, AB = 5 cm,则 AC =_____cm, BD =_____cm.
A
B
C
D
6
10
5
5. 如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1 + ∠2 的度数是________.
90°
6. 如图,AB、CD 相交于点 O,AC⊥CD 于点 C,若∠BOD = 38,则∠A = _____°.
52
第5题图
第6题图
7. 如图,在 Rt△ABC 中,∠ACB = 90°,D 是 AB 上一点,且∠ACD = ∠B.求证:△ACD 是直角三角形.
证明:∵∠ACB = 90°,
∴∠A +∠B = 90°.
∵∠ACD = ∠B,
∴∠A +∠ACD = 90°.
∴△ACD 是直角三角形.
解:(1)∵AD 是△ABC 的高,E、F 分别是 AB、AC 的中点,∴DE=AE= AB= ×10=5,
DF=AF= AC= ×8=4.
∴四边形 AEDF 的周长= AE+DE+DF+AF
= 5+5+4+4 = 18.
8. 如图,在 △ABC 中,AD 是高,E、F 分别是
AB、AC 的中点.
(1) 若AB = 10,AC = 8,求四边形 AEDF 的周长;
(2)求证:EF 垂直平分 AD.
证明:∵DE = AE,DF = AF,
∴E、F 在线段 AD 的垂直平分线上.
∴EF 垂直平分 AD.
归纳:当已知条件含有线段的中点、直角三角形时,可联想到直角三角形斜边上的中线的性质进行求解.
小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
直角三角形斜边上的中线等于斜边的一半.
第1章 直角三角形
1.1 直角三角形的性质和判定(I)
第1课时 直角三角形的性质和判定
学习目标
1.了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余;直角三角形斜边上的中线等于斜边的一半.
2.掌握有两个角互余的三角形是直角三角形.
学习重点、难点
直角三角形的性质定理(直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半).
会判定一个三角形是直角三角形.
重点:
难点:
性质定理“直角三角形斜边上的中线等于斜边的一半”的探索推导过程.
知识回顾
我们已经学习了三角形边与边,边与角,角与角之间的一些性质,你能列举出一些吗?
直角三角形作为一种特殊的三角形,除了具有一般三角形的性质外,它还具有哪些特殊性质呢?
如:三角形内角和为180°……
课时导入
如图所示是我们常用的三角板,它们两锐角的度数之和分别为多少
说一说
30° + 60° = 90°
45° + 45° = 90°
如图,在 Rt△ABC 中,∠C = 90°,两锐角的和等于多少呢?
在 Rt△ABC 中,由三角形内角和定理,得∠A +∠B +∠C = 180°,因为 ∠C = 90°,故∠A + ∠B = 90°.
思考:由此,你可以得到直角三角形有什么性质呢?
知识讲解
直角三角形的性质:
直角三角形的两个锐角互余.
应用:
在 Rt△ABC 中,
∵∠C = 90°,∴∠A +∠B = 90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形 ABC 可以写成 Rt△ABC .
A
B
C
如图,在 △ABC 中, ∠A +∠B = 90°, 那么 △ABC 是直角三角形吗?
有两个锐角互余的三角形是直角三角形吗?
在 △ABC 中,
∵ ∠A +∠B +∠C = 180°, 又∠A +∠B = 90°,
∴∠C = 90°.
于是 △ABC 是直角三角形.
说一说
知识讲解
直角三角形的判定:
有两个角互余的三角形是直角三角形.
应用:
在 △ABC 中,
∵ ∠A +∠B = 90°,
∴ △ABC 是直角三角形.
A
B
C
探究
如图,画一个 Rt△ABC, 并作出斜边 AB 上的中线 CD,比较线段 CD 与线段 AB 之间长度,你能得出什么结论?
我测量后发现
CD = AB.
线段 CD 比线段 AB 短.
猜想:直角三角形斜边上的中线等于斜边的一半.
试给出数学证明.
图1-4
如图 1-3, 如果中线 CD = AB,则有∠DCA = ∠A .
由此受到启发,在图 1-4 的 Rt△ABC 中,过直角顶点 C 作射线 CD′ 交 AB 于 D′,使∠D′CA = ∠A ,则 CD′ = AD′ .
图1-3
证一证
∴ 点 D' 是斜边上的中点,即 CD' 是斜边 AB 的中线.
又∵∠A +∠B = 90°,∠D′CA +∠D′CB = 90°,
∴ ∠B = ∠D′CB.
∴CD′ = BD′.
故得
从而 CD 与 CD' 重合,由此得到:
性质:直角三角形斜边上的中线等于斜边的一半.
例
如图,已知 CD 是 △ABC 的 AB 边上的中线,且 . 求证:△ABC 是直角三角形.
证明:
∴ ∠1 = ∠A,∠2 = ∠B .
∵∠A +∠B +∠ACB = 180°,∠ACB = ∠1 + ∠2,
∴∠A +∠B +∠1 +∠2 = 180°,
∴ 2(∠A +∠B) = 180°.
∴ ∠A +∠B = 90°.
∴ △ABC 是直角三角形.
随 堂 小 测
1. 在一个直角三角形中,有一个锐角等于 40°,则另一个锐角的度数是( )
A.40° B.50°
C.60° D.70°
B
2. 具备下列条件的 △ABC 中,不是直角三角形的是( )
A.∠A + ∠B = ∠C
B.∠A - ∠B = ∠C
C.∠A∶∠B∶∠C = 1∶2∶3
D.∠A = ∠B = 3∠C
D
3. 如图所示,△ABC 为直角三角形,∠ACB = 90°,
CD⊥AB,与 ∠1 互余的角有( )
A.∠B
B.∠A
C.∠BCD 和 ∠A
D.∠BCD
C
4. 如图,在 △ABC 中,∠ABC = 90°,BD 是斜边 AC 上的中线.
(1)若 BD = 3 cm,则 AC =_____cm;
(2)若∠C = 30°, AB = 5 cm,则 AC =_____cm, BD =_____cm.
A
B
C
D
6
10
5
5. 如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1 + ∠2 的度数是________.
90°
6. 如图,AB、CD 相交于点 O,AC⊥CD 于点 C,若∠BOD = 38,则∠A = _____°.
52
第5题图
第6题图
7. 如图,在 Rt△ABC 中,∠ACB = 90°,D 是 AB 上一点,且∠ACD = ∠B.求证:△ACD 是直角三角形.
证明:∵∠ACB = 90°,
∴∠A +∠B = 90°.
∵∠ACD = ∠B,
∴∠A +∠ACD = 90°.
∴△ACD 是直角三角形.
解:(1)∵AD 是△ABC 的高,E、F 分别是 AB、AC 的中点,∴DE=AE= AB= ×10=5,
DF=AF= AC= ×8=4.
∴四边形 AEDF 的周长= AE+DE+DF+AF
= 5+5+4+4 = 18.
8. 如图,在 △ABC 中,AD 是高,E、F 分别是
AB、AC 的中点.
(1) 若AB = 10,AC = 8,求四边形 AEDF 的周长;
(2)求证:EF 垂直平分 AD.
证明:∵DE = AE,DF = AF,
∴E、F 在线段 AD 的垂直平分线上.
∴EF 垂直平分 AD.
归纳:当已知条件含有线段的中点、直角三角形时,可联想到直角三角形斜边上的中线的性质进行求解.
小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
直角三角形斜边上的中线等于斜边的一半.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
