1.1 直角三角形的性质和判定(I)第2课时 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 1.1 直角三角形的性质和判定(I)第2课时 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第1章 直角三角形
1.1 直角三角形的性质和判定(I)
第2课时 含30°角的直角三角形的性质及其应用
课时导入
问题引入
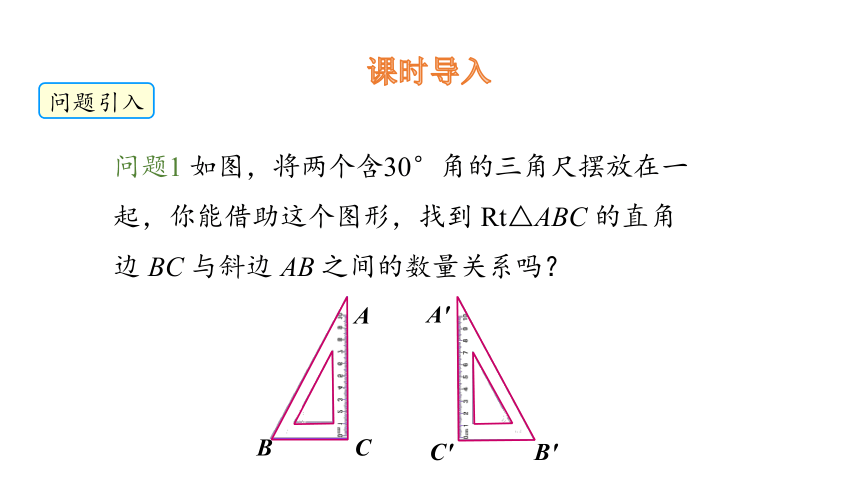
问题1 如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到 Rt△ABC 的直角边 BC 与斜边 AB 之间的数量关系吗?
A
C
B'
A'
C'
B
问题2 剪一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
动手:用刻度尺测量含 30°角的直角三角形的斜边和短直角边,比较它们之间的数量关系.
结论:短直角边=斜边
证明1:取线段 AB 的中点 D,连接 CD.
∵CD 为 Rt△ABC 斜边 AB 上的中线,
A
30°
B
C
D
∵∠BCA = 90°,且 ∠A = 30°,
∴∠B = 60°.
∴△CBD 为等边三角形.
证明方法:中线法
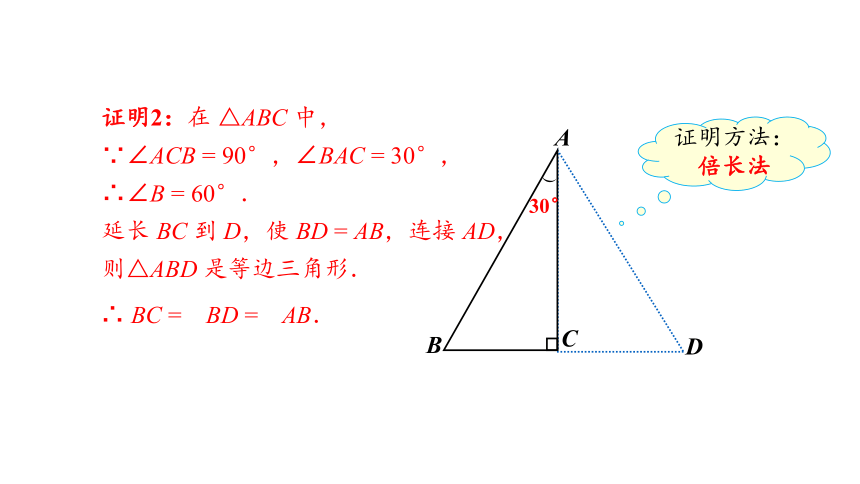
证明2:在 △ABC 中,
∵∠ACB = 90°,∠BAC = 30°,
∴∠B = 60°.
延长 BC 到 D,使 BD = AB,连接 AD,
则△ABD 是等边三角形.
A
B
C
D
∴ BC = BD = AB.
30°
)
证明方法:倍长法
)
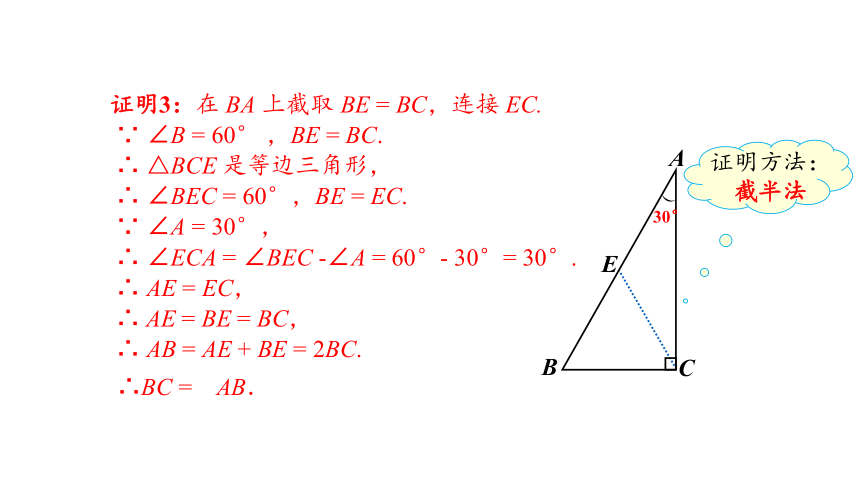
证明3:在 BA 上截取 BE = BC,连接 EC.
∵ ∠B = 60° ,BE = BC.
∴ △BCE 是等边三角形,
∴ ∠BEC = 60°,BE = EC.
∵ ∠A = 30°,
∴ ∠ECA = ∠BEC -∠A = 60°- 30°= 30°.
∴ AE = EC,
∴ AE = BE = BC,
∴ AB = AE + BE = 2BC.
E
A
B
C
∴BC = AB.
30°
证明方法:截半法
知识讲解
含30°角的直角三角形的性质:
在直角三角形中,如果一锐角等于30°,那么这个锐角所对的直角边等于斜边的一半.
应用:
∵在 Rt△ABC 中,∠C = 90°,∠A = 30°,
A
B
C
)
30°
如图,在 Rt△ABC 中,如果 BC = AB,那么 ∠A 等于多少?
动脑筋
解:如图,取线段 AB 的中点 D,连接 CD.
∵CD 是 Rt△ABC 斜边 AB 上的中线,
即△BDC 为等边三角形.
∴∠B = 60°.
∵∠B +∠A = 90°,
∴∠A = 30°.
B
C
A
D
知识讲解
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于 30°.
应用:
∵ 在 Rt△ABC 中,∠C = 90°,BC = AB.
∴∠A = 30°.
A
B
C
)
30°
例
解:∵∠AOD = 30°,
AO = 海里,
∴ AD = AO = 海里>20 海里,
∴无触礁危险.
O
B
D
A
北
东
60°
如图,在 A 岛周围 20 海里 (1 海里 = 1 852 m) 水域内有暗礁,一轮船由西向东航行到 O 处时,测得 A 岛在北偏东 60°的方向上,且与轮船相距 海里.若该船继续保持航向不变,有触礁的危险吗?
随 堂 小 测
B
1. 如图,在 Rt△ABC 中,∠ACB=90°,∠B=30°,CD 是斜边 AB 上的高,AD=3 cm,则 AB 的长度是( )
A.3 cm B.6 cm
C.9 cm D.12 cm
注意:运用含 30°角的直角三角形的性质求线段长时,要分清线段所在的直角三角形.
2. 如图,一棵树在一次强台风中,于离地面 3 米处折断倒下,倒下部分与地面成 30°角,这棵树在折断前的高度为( )
A.6 米 B.9 米
C.12 米 D.15 米
B
3. 某市在旧城改造中,计划在一块如图所示的 △ABC 空地上种植草皮以美化环境,已知∠A = 150°,这种草皮每平方米售价 a 元,则购买这种草皮需要 ( )
A.300a 元 B.150a 元
C.450a 元 D.225a 元
B
4. 如图,在 △ABC 中,∠ACB = 90°,CD 是高,
∠A = 30°,AB = 4.则 BD 的长为 .
1
A
B
C
D
5. 如图,Rt△ABC 中,∠A = 30°,AB + BC = 12 cm,则 AB =______cm.
A
C
B
第5题图
第4题图
8
∵∠B = ∠ACB = 15° (已知),
∴∠DAC = ∠B+∠ACB = 15°+15°= 30°,
6. 已知:等腰三角形的底角为 15°,腰长为 20. 求腰上的高.
A
C
B
D
15°
15°
20
解:过 C 作 CD⊥BA 交 BA 的延长线于点 D.
)
)
∴CD = AC = ×20 = 10.
方法总结:在求三角形边长的一些问题中,可以构造含 30°角的直角三角形来解决.
7. 如图所示,在四边形 ACBD 中,AD∥BC,
AB⊥AC,且 AC = BC,求∠DAC 的度数.
解:∵AB⊥AC,
∴∠CAB = 90°.
∵AC = BC,
∴∠CBA = 30°.
∵AD∥BC,
∴∠BAD = ∠CBA =30°.
∴∠DAC = ∠CAB+∠BAD = 120°.
A
B
C
D
E
解:∵DE⊥AC,BC ⊥AC,∠A = 30°,
∴BC = AB,DE = AD.
∴BC = AB = ×7.4 = 3.7(m).
又AD = AB,
∴DE = AD = ×3.7 = 1.85 (m).
答:立柱 BC 的长是 3.7 m,DE 的长是 1.85 m.
8.如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC、DE 有多长?
小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
直角三角形斜边上的中线等于斜边的一半.
小结
内容
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半(反之亦成立)
使用要点
含 30°角的直角三角形的性质
找准 30°的角所对的直角边,点明斜边
注意
前提条件:含30°角的直角三角形中
第1章 直角三角形
1.1 直角三角形的性质和判定(I)
第2课时 含30°角的直角三角形的性质及其应用
课时导入
问题引入
问题1 如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到 Rt△ABC 的直角边 BC 与斜边 AB 之间的数量关系吗?
A
C
B'
A'
C'
B
问题2 剪一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
动手:用刻度尺测量含 30°角的直角三角形的斜边和短直角边,比较它们之间的数量关系.
结论:短直角边=斜边
证明1:取线段 AB 的中点 D,连接 CD.
∵CD 为 Rt△ABC 斜边 AB 上的中线,
A
30°
B
C
D
∵∠BCA = 90°,且 ∠A = 30°,
∴∠B = 60°.
∴△CBD 为等边三角形.
证明方法:中线法
证明2:在 △ABC 中,
∵∠ACB = 90°,∠BAC = 30°,
∴∠B = 60°.
延长 BC 到 D,使 BD = AB,连接 AD,
则△ABD 是等边三角形.
A
B
C
D
∴ BC = BD = AB.
30°
)
证明方法:倍长法
)
证明3:在 BA 上截取 BE = BC,连接 EC.
∵ ∠B = 60° ,BE = BC.
∴ △BCE 是等边三角形,
∴ ∠BEC = 60°,BE = EC.
∵ ∠A = 30°,
∴ ∠ECA = ∠BEC -∠A = 60°- 30°= 30°.
∴ AE = EC,
∴ AE = BE = BC,
∴ AB = AE + BE = 2BC.
E
A
B
C
∴BC = AB.
30°
证明方法:截半法
知识讲解
含30°角的直角三角形的性质:
在直角三角形中,如果一锐角等于30°,那么这个锐角所对的直角边等于斜边的一半.
应用:
∵在 Rt△ABC 中,∠C = 90°,∠A = 30°,
A
B
C
)
30°
如图,在 Rt△ABC 中,如果 BC = AB,那么 ∠A 等于多少?
动脑筋
解:如图,取线段 AB 的中点 D,连接 CD.
∵CD 是 Rt△ABC 斜边 AB 上的中线,
即△BDC 为等边三角形.
∴∠B = 60°.
∵∠B +∠A = 90°,
∴∠A = 30°.
B
C
A
D
知识讲解
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于 30°.
应用:
∵ 在 Rt△ABC 中,∠C = 90°,BC = AB.
∴∠A = 30°.
A
B
C
)
30°
例
解:∵∠AOD = 30°,
AO = 海里,
∴ AD = AO = 海里>20 海里,
∴无触礁危险.
O
B
D
A
北
东
60°
如图,在 A 岛周围 20 海里 (1 海里 = 1 852 m) 水域内有暗礁,一轮船由西向东航行到 O 处时,测得 A 岛在北偏东 60°的方向上,且与轮船相距 海里.若该船继续保持航向不变,有触礁的危险吗?
随 堂 小 测
B
1. 如图,在 Rt△ABC 中,∠ACB=90°,∠B=30°,CD 是斜边 AB 上的高,AD=3 cm,则 AB 的长度是( )
A.3 cm B.6 cm
C.9 cm D.12 cm
注意:运用含 30°角的直角三角形的性质求线段长时,要分清线段所在的直角三角形.
2. 如图,一棵树在一次强台风中,于离地面 3 米处折断倒下,倒下部分与地面成 30°角,这棵树在折断前的高度为( )
A.6 米 B.9 米
C.12 米 D.15 米
B
3. 某市在旧城改造中,计划在一块如图所示的 △ABC 空地上种植草皮以美化环境,已知∠A = 150°,这种草皮每平方米售价 a 元,则购买这种草皮需要 ( )
A.300a 元 B.150a 元
C.450a 元 D.225a 元
B
4. 如图,在 △ABC 中,∠ACB = 90°,CD 是高,
∠A = 30°,AB = 4.则 BD 的长为 .
1
A
B
C
D
5. 如图,Rt△ABC 中,∠A = 30°,AB + BC = 12 cm,则 AB =______cm.
A
C
B
第5题图
第4题图
8
∵∠B = ∠ACB = 15° (已知),
∴∠DAC = ∠B+∠ACB = 15°+15°= 30°,
6. 已知:等腰三角形的底角为 15°,腰长为 20. 求腰上的高.
A
C
B
D
15°
15°
20
解:过 C 作 CD⊥BA 交 BA 的延长线于点 D.
)
)
∴CD = AC = ×20 = 10.
方法总结:在求三角形边长的一些问题中,可以构造含 30°角的直角三角形来解决.
7. 如图所示,在四边形 ACBD 中,AD∥BC,
AB⊥AC,且 AC = BC,求∠DAC 的度数.
解:∵AB⊥AC,
∴∠CAB = 90°.
∵AC = BC,
∴∠CBA = 30°.
∵AD∥BC,
∴∠BAD = ∠CBA =30°.
∴∠DAC = ∠CAB+∠BAD = 120°.
A
B
C
D
E
解:∵DE⊥AC,BC ⊥AC,∠A = 30°,
∴BC = AB,DE = AD.
∴BC = AB = ×7.4 = 3.7(m).
又AD = AB,
∴DE = AD = ×3.7 = 1.85 (m).
答:立柱 BC 的长是 3.7 m,DE 的长是 1.85 m.
8.如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC、DE 有多长?
小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
直角三角形斜边上的中线等于斜边的一半.
小结
内容
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半(反之亦成立)
使用要点
含 30°角的直角三角形的性质
找准 30°的角所对的直角边,点明斜边
注意
前提条件:含30°角的直角三角形中
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
