1.2 直角三角形的性质和判定(II)第2课时 课件(共17张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 1.2 直角三角形的性质和判定(II)第2课时 课件(共17张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 302.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第1章 直角三角形
1.1 直角三角形的性质和判定(II)
第2课时 勾股定理的应用
课时导入
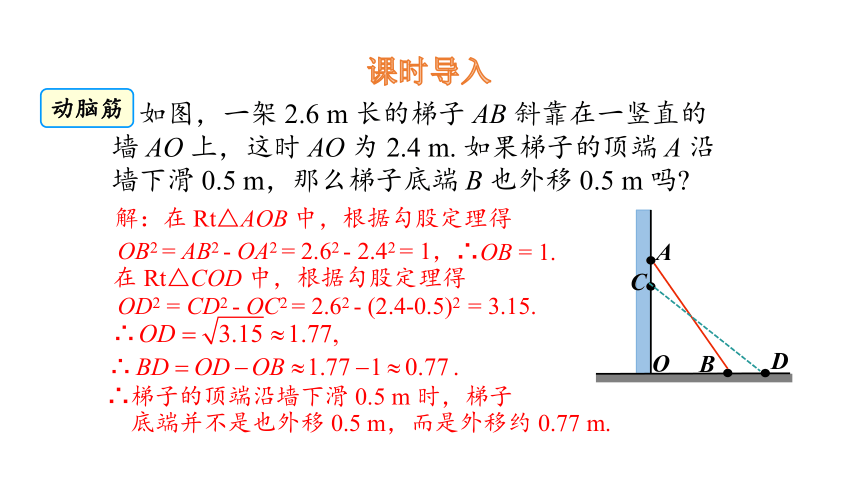
如图,一架 2.6 m 长的梯子 AB 斜靠在一竖直的墙 AO 上,这时 AO 为 2.4 m. 如果梯子的顶端 A 沿墙下滑 0.5 m,那么梯子底端 B 也外移 0.5 m 吗
动脑筋
A
B
D
C
O
解:在 Rt△AOB 中,根据勾股定理得
OB2 = AB2 - OA2 = 2.62 - 2.42 = 1,
∴OB = 1.
在 Rt△COD 中,根据勾股定理得
OD2 = CD2 - OC2 = 2.62 - (2.4-0.5)2 = 3.15.
∴梯子的顶端沿墙下滑 0.5 m 时,梯子
底端并不是也外移 0.5 m,而是外移约 0.77 m.
我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为 10 尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
B
C
A
例
解:设水池的水深 AC 为 x 尺,
则这根芦苇长 AD = AB = (x+1)尺,
在直角三角形 ABC 中,BC = 5 尺,
由勾股定理得,BC2 + AC2 = AB2,
即 52 + x2 = (x+1)2,
25 + x2 = x2 + 2x + 1,
2x = 24,
∴ x = 12,x + 1 = 13.
答:水池的水深 12 尺,这根芦苇长 13 尺.
D
B
C
A
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
知识讲解
利用勾股定理解决实际问题的一般步骤:
探究1
有一个圆柱形油罐,要以 A 点环绕油罐建梯子,正好建在 A 点的正上方点 B 处,问梯子最短需多少米(已知油罐的底面半径是 2 m,高 AB 是 5 m,π 取 3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则 AB' 为梯子的最短距离.
AA' = 2×3×2 = 12, A'B' = 5,根据勾股定理得
即梯子最短需 13 米.
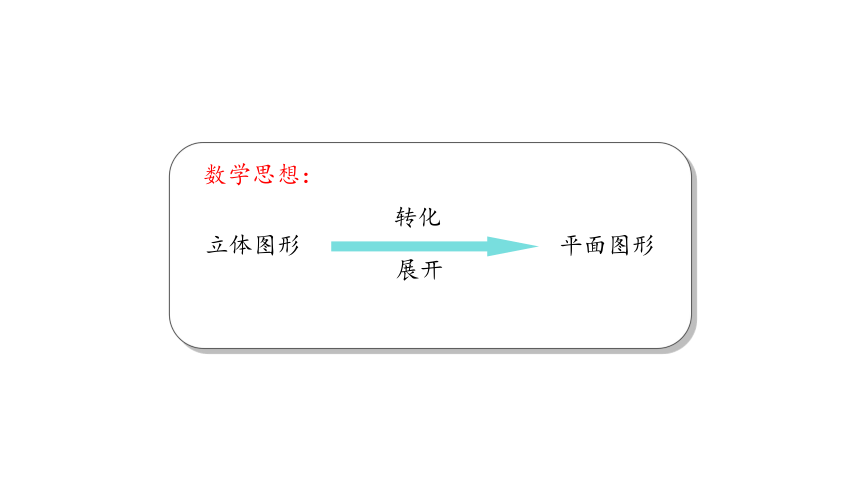
归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
数学思想:
立体图形
平面图形
转化
展开
探究2
如图,一个牧童在小河的南 4 km 的 A 处牧马,而他正位于他的小屋 B 的西 8 km 北 7 km 处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
解:如图,作出点 A 关于河岸的对称点 A′,
连接 A′B,则 A′B 的长就是最短路程.
由题意得 A′C = 4 + 4 + 7 = 15 (km),
BC = 8 km.
在 Rt△A′CB 中,由勾股定理得
即最短路程是17 km.
牧童
A
小屋 B
A′
C
东
北
归纳:求直线同侧的两定点到直线上一动点的距离之和最小的方法:先作其中一定点关于这条直线的对称点,连接对称点与另一定点的线段的长就是最小的距离之和,以此线段为斜边构造直角三角形,再结合勾股定理就能求出这个最小的距离和.
随 堂 小 测
1. 从电线杆上离地面 5 m 的 C 处向地面拉一条长为 7 m的钢缆,则地面钢缆 A 到电线杆底部 B 的距离是( )
A. 24 m B. 12 m C. m D. m
D
2. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是 9 cm,内壁高 12 cm,则这只铅笔的长度可能是( )
A.9 cm B.12 cm C.15 cm D.18 cm
D
A
B
C
A.50 米 B.120 米 C.100 米 D.130 米
130
120
A
3. 湖的两端有 A,B 两点,从与 BA 方向成直角的 BC 方向上的点 C 测得 CA =130 米,CB =120 米,则 AB 为( )
4. 在一次台风的袭击中,小明家房前的一棵大树在离地面 6 米处断裂,树的顶部落在离树根底部 8 米处.你能告诉小明这棵树折断之前有多高吗?
8 米
6米
A
C
B
解:根据题意构建直角三角形,如图.
在 Rt△ABC 中,AC = 6 米,BC = 8 米,
由勾股定理得
∴这棵树在折断之前的高度是10+6 = 16(米).
B
牛奶盒
A
5. 看到小蚂蚁终于找到食物的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点 A 处,并在点 B 处放了一滴蜂蜜,你能帮小蚂蚁求出找到蜂蜜的最短路程么?
6 cm
8 cm
10 cm
B
B1
8
A
B2
6
10
B3
AB12 =102 + (6+8)2 = 296,
AB22= 82 + (10+6)2 = 320,
AB32= 62 + (10+8)2 = 360,
解:由题意知有三种展开方法,
如图.由勾股定理得
∴ AB1<AB2<AB3.
∴小蚂蚁找到蜂蜜的最短路程为 AB1,长为 cm .
解:(1) 在 Rt△ ABC 中,根据勾股定理得
∴这条“近路”的长为 5 米.
C
A
B
6. 如图,学校教学楼前有一块长为 4 米,宽为 3 米的长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“近路”,却踩伤了花草.
(1) 求这条“近路”的长;
(2) 他们仅仅少走了几步(假设 2 步为 1 米)?
(2) 他们仅仅少走了
(3 + 4 - 5)×2 = 4 (步).
小结
勾股定理
的应用
用勾股定理解决实际问题
用勾股定理解决点的距离及路径最短问题
第1章 直角三角形
1.1 直角三角形的性质和判定(II)
第2课时 勾股定理的应用
课时导入
如图,一架 2.6 m 长的梯子 AB 斜靠在一竖直的墙 AO 上,这时 AO 为 2.4 m. 如果梯子的顶端 A 沿墙下滑 0.5 m,那么梯子底端 B 也外移 0.5 m 吗
动脑筋
A
B
D
C
O
解:在 Rt△AOB 中,根据勾股定理得
OB2 = AB2 - OA2 = 2.62 - 2.42 = 1,
∴OB = 1.
在 Rt△COD 中,根据勾股定理得
OD2 = CD2 - OC2 = 2.62 - (2.4-0.5)2 = 3.15.
∴梯子的顶端沿墙下滑 0.5 m 时,梯子
底端并不是也外移 0.5 m,而是外移约 0.77 m.
我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为 10 尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
B
C
A
例
解:设水池的水深 AC 为 x 尺,
则这根芦苇长 AD = AB = (x+1)尺,
在直角三角形 ABC 中,BC = 5 尺,
由勾股定理得,BC2 + AC2 = AB2,
即 52 + x2 = (x+1)2,
25 + x2 = x2 + 2x + 1,
2x = 24,
∴ x = 12,x + 1 = 13.
答:水池的水深 12 尺,这根芦苇长 13 尺.
D
B
C
A
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
知识讲解
利用勾股定理解决实际问题的一般步骤:
探究1
有一个圆柱形油罐,要以 A 点环绕油罐建梯子,正好建在 A 点的正上方点 B 处,问梯子最短需多少米(已知油罐的底面半径是 2 m,高 AB 是 5 m,π 取 3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则 AB' 为梯子的最短距离.
AA' = 2×3×2 = 12, A'B' = 5,根据勾股定理得
即梯子最短需 13 米.
归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
数学思想:
立体图形
平面图形
转化
展开
探究2
如图,一个牧童在小河的南 4 km 的 A 处牧马,而他正位于他的小屋 B 的西 8 km 北 7 km 处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
解:如图,作出点 A 关于河岸的对称点 A′,
连接 A′B,则 A′B 的长就是最短路程.
由题意得 A′C = 4 + 4 + 7 = 15 (km),
BC = 8 km.
在 Rt△A′CB 中,由勾股定理得
即最短路程是17 km.
牧童
A
小屋 B
A′
C
东
北
归纳:求直线同侧的两定点到直线上一动点的距离之和最小的方法:先作其中一定点关于这条直线的对称点,连接对称点与另一定点的线段的长就是最小的距离之和,以此线段为斜边构造直角三角形,再结合勾股定理就能求出这个最小的距离和.
随 堂 小 测
1. 从电线杆上离地面 5 m 的 C 处向地面拉一条长为 7 m的钢缆,则地面钢缆 A 到电线杆底部 B 的距离是( )
A. 24 m B. 12 m C. m D. m
D
2. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是 9 cm,内壁高 12 cm,则这只铅笔的长度可能是( )
A.9 cm B.12 cm C.15 cm D.18 cm
D
A
B
C
A.50 米 B.120 米 C.100 米 D.130 米
130
120
A
3. 湖的两端有 A,B 两点,从与 BA 方向成直角的 BC 方向上的点 C 测得 CA =130 米,CB =120 米,则 AB 为( )
4. 在一次台风的袭击中,小明家房前的一棵大树在离地面 6 米处断裂,树的顶部落在离树根底部 8 米处.你能告诉小明这棵树折断之前有多高吗?
8 米
6米
A
C
B
解:根据题意构建直角三角形,如图.
在 Rt△ABC 中,AC = 6 米,BC = 8 米,
由勾股定理得
∴这棵树在折断之前的高度是10+6 = 16(米).
B
牛奶盒
A
5. 看到小蚂蚁终于找到食物的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点 A 处,并在点 B 处放了一滴蜂蜜,你能帮小蚂蚁求出找到蜂蜜的最短路程么?
6 cm
8 cm
10 cm
B
B1
8
A
B2
6
10
B3
AB12 =102 + (6+8)2 = 296,
AB22= 82 + (10+6)2 = 320,
AB32= 62 + (10+8)2 = 360,
解:由题意知有三种展开方法,
如图.由勾股定理得
∴ AB1<AB2<AB3.
∴小蚂蚁找到蜂蜜的最短路程为 AB1,长为 cm .
解:(1) 在 Rt△ ABC 中,根据勾股定理得
∴这条“近路”的长为 5 米.
C
A
B
6. 如图,学校教学楼前有一块长为 4 米,宽为 3 米的长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“近路”,却踩伤了花草.
(1) 求这条“近路”的长;
(2) 他们仅仅少走了几步(假设 2 步为 1 米)?
(2) 他们仅仅少走了
(3 + 4 - 5)×2 = 4 (步).
小结
勾股定理
的应用
用勾股定理解决实际问题
用勾股定理解决点的距离及路径最短问题
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
