1.3 直角三角形全等的判定 课件(共21张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 1.3 直角三角形全等的判定 课件(共21张PPT) 2023-2024学年数学湘教版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 892.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 11:57:09 | ||
图片预览






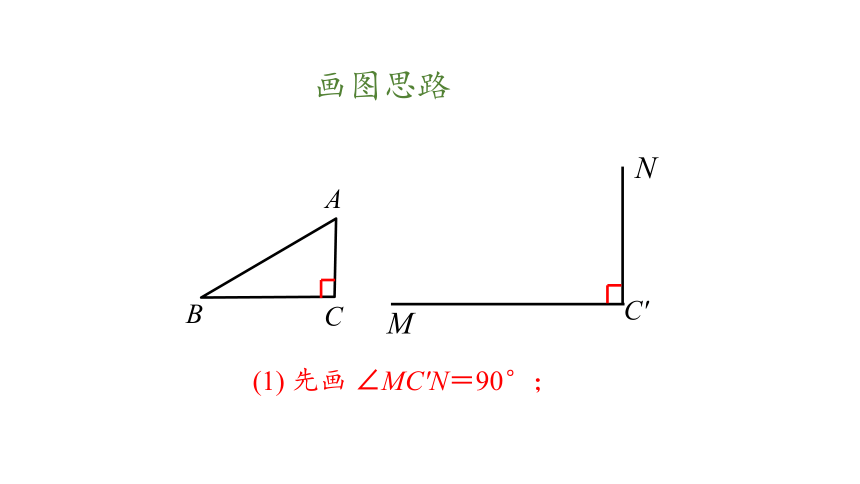
文档简介
(共21张PPT)
第1章 直角三角形
1.3 直角三角形全等的判定
学习目标
探索并掌握判定直角三角形全等的“斜边、直角边”定理.
学习重点、难点
运用“斜边、直角边”定理证明两个直角三角形全等.
重点:
难点:
“斜边、直角边”定理的探索推导过程.
知识回顾
我们已经学过的判定三角形全等的方法有:
SSS ASA
SAS AAS
课时导入
思考
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
A
B
C
A′
B′
C′
1. 两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2. 两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
3. 两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
任意画一个Rt△ABC,使∠C = 90°.再画一个 Rt△A′B′C′,使∠C′ = 90°,B′C′ = BC,A′B′ = AB,把画好的Rt△A′B′ C′ 剪下来,放到 Rt△ABC 上,它们能重合吗?
A
B
C
探究
画图思路
(1) 先画 ∠MC′N=90°;
A
B
C
M
C′
N
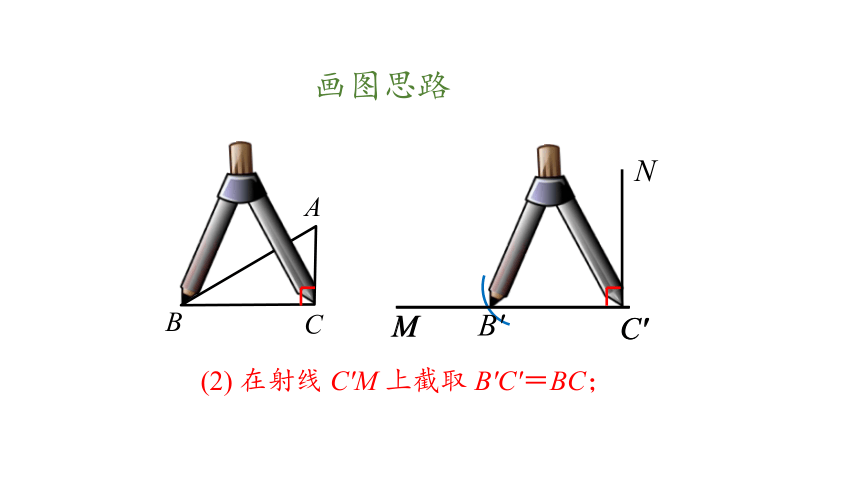
(2) 在射线 C′M 上截取 B′C′=BC;
M
C′
A
B
C
N
B′
M
C′
画图思路
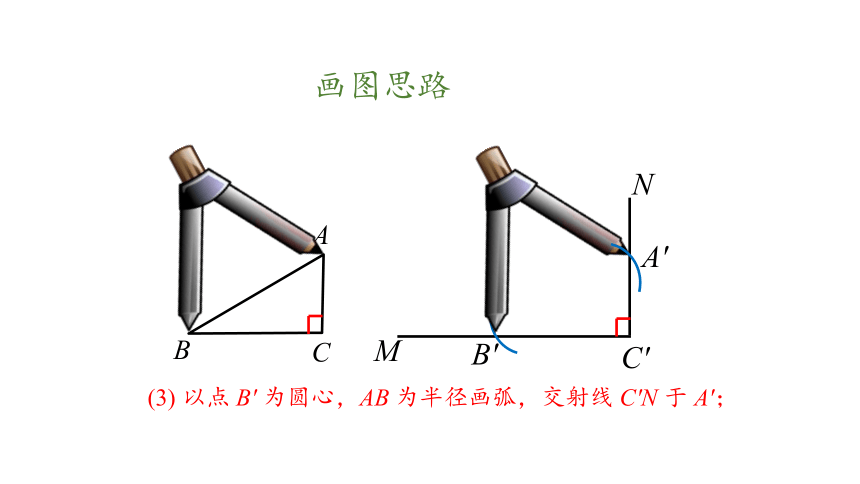
(3) 以点 B′ 为圆心,AB 为半径画弧,交射线 C′N 于 A′;
M
C′
A
B
C
N
B′
A′
画图思路
(4) 连接 A′B′.
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
画图思路
B
C
A
A'
B'
C'
在 Rt△ABC 和 Rt△A'B'C' 中,∵AB = A'B',AC = A'C',
根据勾股定理,
BC2 = AB2-AC2,
B'C'2 = A'B'2-A'C'2,
∴BC = B'C'.
∴Rt△ABC ≌ Rt△A'B'C'.
证明猜想
知识讲解
“斜边、直角边”定理:
斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A′
B′
C′
在 Rt△ABC 和 Rt△A′B′C′ 中,
∴ Rt△ABC≌Rt△A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
例
如图,BD,CE分别是△ABC的高,且BE=CD.
求证:Rt△BEC ≌ Rt△CDB.
证明:∵ BD,CE是△ABC的高,
∴∠BEC = ∠CDB = 90°.
在 Rt△BEC 和Rt△CDB 中,
∵BC = CB,BE = CD,
∴ Rt△BEC≌Rt△CDB (HL).
A
B
C
E
D
随 堂 小 测
1. 判断两个直角三角形全等的方法不正确的有 ( )
A. 两条直角边对应相等
B. 斜边和一锐角对应相等
C. 斜边和一条直角边对应相等
D. 两个锐角对应相等
D
A
2. 如图,在 △ABC 中,AD ⊥ BC 于点 D,CE ⊥ AB 于
点 E ,AD,CE 交于点 H,已知 EH = EB = 3,
AE = 4,则 CH 的长为 ( )
A.1 B.2 C.3 D.4
3.如图,已知 AD,AF 分别是两个钝角 △ABC 和△ABE 的高,如果 AD = AF ,AC =AE. 求证:BC = BE.
证明:∵AD,AF 分别是两个钝角 △ABC 和 △ABE 的高,且 AD = AF,AC = AE,
∴ Rt△ADC≌Rt△AFE (HL).
∴ CD = EF.
∵AD = AF,AB = AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD = BF.
∴BD-CD = BF-EF. 即 BC = BE.
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”定理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
4. 如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的长度 DF 相等,两个滑梯的倾斜角 ∠B 和 ∠F 的大小有什么关系?
解:在 Rt△ABC 和 Rt△DEF 中,
BC = EF,
AC = DF,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B = ∠DEF (全等三角形对应角相等).
∵ ∠DEF +∠F = 90°,
∴∠B +∠F = 90°.
5. 如图,有一直角三角形 ABC,∠C = 90°,AC = 10 cm,BC = 5 cm,一条线段 PQ = AB,P、Q 两点分别在 AC 上和过 A 点且垂直于 AC 的射线 AQ 上运动,问 P 点运动到 AC 上什么位置时 △ABC 才能和△APQ 全等?
解:(1) 当 P 运动到 AP=BC 时,
∵∠C=∠QAP=90°.
在 Rt△ABC 与 Rt△QPA 中,
∵ PQ = AB,AP = BC,
∴ Rt△ABC≌Rt△QPA (HL),
∴AP = BC = 5 cm.
(2)当 P 运动到与 C 点重合时,AP = AC.
在 Rt△ABC 与 Rt△PQA 中,
∵PQ = AB,AP = AC,
∴Rt△PQA≌Rt△ABC (HL),
∴AP = AC = 10 cm,
∴当AP=5 cm 或10 cm 时,△ABC 才能和△PQA 全等.
方法总结:判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
小结
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等
前提条件
在直角三角形中
第1章 直角三角形
1.3 直角三角形全等的判定
学习目标
探索并掌握判定直角三角形全等的“斜边、直角边”定理.
学习重点、难点
运用“斜边、直角边”定理证明两个直角三角形全等.
重点:
难点:
“斜边、直角边”定理的探索推导过程.
知识回顾
我们已经学过的判定三角形全等的方法有:
SSS ASA
SAS AAS
课时导入
思考
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
A
B
C
A′
B′
C′
1. 两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2. 两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
3. 两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
任意画一个Rt△ABC,使∠C = 90°.再画一个 Rt△A′B′C′,使∠C′ = 90°,B′C′ = BC,A′B′ = AB,把画好的Rt△A′B′ C′ 剪下来,放到 Rt△ABC 上,它们能重合吗?
A
B
C
探究
画图思路
(1) 先画 ∠MC′N=90°;
A
B
C
M
C′
N
(2) 在射线 C′M 上截取 B′C′=BC;
M
C′
A
B
C
N
B′
M
C′
画图思路
(3) 以点 B′ 为圆心,AB 为半径画弧,交射线 C′N 于 A′;
M
C′
A
B
C
N
B′
A′
画图思路
(4) 连接 A′B′.
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
画图思路
B
C
A
A'
B'
C'
在 Rt△ABC 和 Rt△A'B'C' 中,∵AB = A'B',AC = A'C',
根据勾股定理,
BC2 = AB2-AC2,
B'C'2 = A'B'2-A'C'2,
∴BC = B'C'.
∴Rt△ABC ≌ Rt△A'B'C'.
证明猜想
知识讲解
“斜边、直角边”定理:
斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A′
B′
C′
在 Rt△ABC 和 Rt△A′B′C′ 中,
∴ Rt△ABC≌Rt△A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
例
如图,BD,CE分别是△ABC的高,且BE=CD.
求证:Rt△BEC ≌ Rt△CDB.
证明:∵ BD,CE是△ABC的高,
∴∠BEC = ∠CDB = 90°.
在 Rt△BEC 和Rt△CDB 中,
∵BC = CB,BE = CD,
∴ Rt△BEC≌Rt△CDB (HL).
A
B
C
E
D
随 堂 小 测
1. 判断两个直角三角形全等的方法不正确的有 ( )
A. 两条直角边对应相等
B. 斜边和一锐角对应相等
C. 斜边和一条直角边对应相等
D. 两个锐角对应相等
D
A
2. 如图,在 △ABC 中,AD ⊥ BC 于点 D,CE ⊥ AB 于
点 E ,AD,CE 交于点 H,已知 EH = EB = 3,
AE = 4,则 CH 的长为 ( )
A.1 B.2 C.3 D.4
3.如图,已知 AD,AF 分别是两个钝角 △ABC 和△ABE 的高,如果 AD = AF ,AC =AE. 求证:BC = BE.
证明:∵AD,AF 分别是两个钝角 △ABC 和 △ABE 的高,且 AD = AF,AC = AE,
∴ Rt△ADC≌Rt△AFE (HL).
∴ CD = EF.
∵AD = AF,AB = AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD = BF.
∴BD-CD = BF-EF. 即 BC = BE.
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”定理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
4. 如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的长度 DF 相等,两个滑梯的倾斜角 ∠B 和 ∠F 的大小有什么关系?
解:在 Rt△ABC 和 Rt△DEF 中,
BC = EF,
AC = DF,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B = ∠DEF (全等三角形对应角相等).
∵ ∠DEF +∠F = 90°,
∴∠B +∠F = 90°.
5. 如图,有一直角三角形 ABC,∠C = 90°,AC = 10 cm,BC = 5 cm,一条线段 PQ = AB,P、Q 两点分别在 AC 上和过 A 点且垂直于 AC 的射线 AQ 上运动,问 P 点运动到 AC 上什么位置时 △ABC 才能和△APQ 全等?
解:(1) 当 P 运动到 AP=BC 时,
∵∠C=∠QAP=90°.
在 Rt△ABC 与 Rt△QPA 中,
∵ PQ = AB,AP = BC,
∴ Rt△ABC≌Rt△QPA (HL),
∴AP = BC = 5 cm.
(2)当 P 运动到与 C 点重合时,AP = AC.
在 Rt△ABC 与 Rt△PQA 中,
∵PQ = AB,AP = AC,
∴Rt△PQA≌Rt△ABC (HL),
∴AP = AC = 10 cm,
∴当AP=5 cm 或10 cm 时,△ABC 才能和△PQA 全等.
方法总结:判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
小结
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等
前提条件
在直角三角形中
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
