2.1 多边形 第2课时 课件(共18张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 2.1 多边形 第2课时 课件(共18张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 983.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 11:58:49 | ||
图片预览





文档简介
(共18张PPT)
第2章 四边形
2.1 多边形
第2课时 多边形的外角和
课时导入
动脑筋
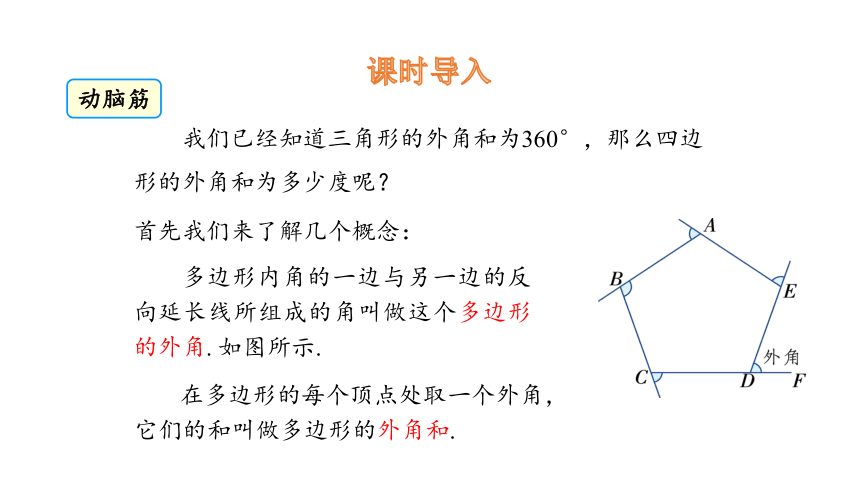
我们已经知道三角形的外角和为360°,那么四边形的外角和为多少度呢?
首先我们来了解几个概念:
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. 如图所示.
在多边形的每个顶点处取一个外角,它们的和叫做多边形的外角和.
如图,在五边形的每个顶点处各取一个外角.
问题1 任意一个外角和它相邻的内角有什么关系?
问题2 五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°= 900°
E
B
C
D
1
2
3
4
5
A
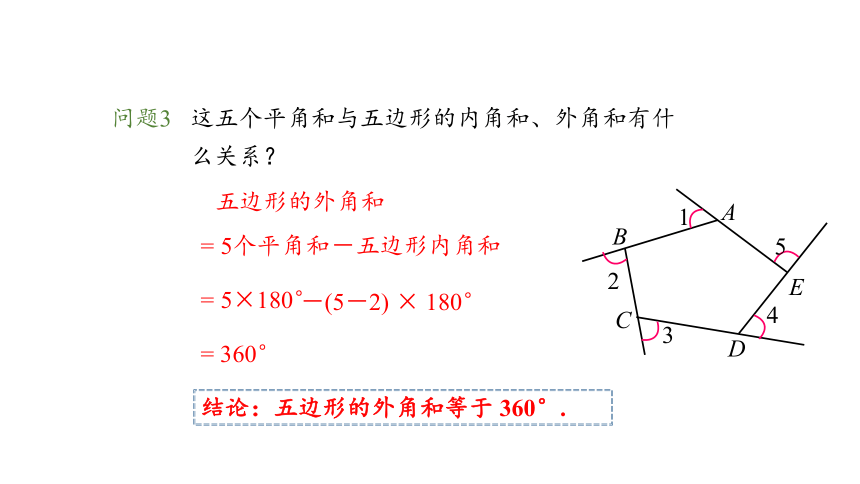
五边形的外角和
= 360°
= 5个平角和
-五边形内角和
= 5×180°
-(5-2) × 180°
结论:五边形的外角和等于 360°.
问题3 这五个平角和与五边形的内角和、外角和有什
么关系?
n 边形外角和
n 边形的外角和等于 360°.
-(n-2) × 180°
= 360°
= n 个平角和- n 边形内角和
= n×180°
An
A2
A3
A4
1
2
3
4
n
A1
n 边形的外角和又是多少呢?
与边数无关
思考
问题4 回想正多边形的性质,你知道正 n 边形的每个
内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
任意多边形的外角和等于360°.
知识讲解
多边形的外角和:
n边形的外角和与边数没有关系.
例
一个多边形的内角和等于它外角和的 5 倍,它是几边形?
解: 设多边形的边数为 n,
则它的内角和等于 (n -2)·180°.
由题意得
(n - 2)·180°= 5×360°,
解得 n = 12.
因此这个多边形是十二边形.
观察
三角形具有稳定性,那么四边形呢?
四边形具有不稳定性:
各边的长确定后,图形形状不能确定.
在实际生活中,我们经常利用四边形的不稳定性,例如图1,2中的电动伸缩门. 有时又要克服四边形的不稳定性,例如在图3中的栅栏两横梁之间加钉斜木条,构成三角形,这是利用了三角形的稳定性.
图1
图2
图3
随 堂 小 测
1. 一个正多边形的内角 135°,则这个正多边形的边数为______.
8
2. 如图所示,小明从点 A 出发,沿直线前进 10 米后左转 24°,再沿直线前进 10 米,又向左转 24°……照这样走下去,他第一次回到出发地点 A 时,走的路程一共是________米.
150
3.已知一个多边形的每个内角与外角的比都是 7∶2,求这个多边形的边数.
方法一:设这个多边形的内角为 7x°,外角为 2x°,
根据题意得
7x + 2x = 180,
解得 x = 20.
即每个内角是 140°,每个外角是 40°.
360°÷40° = 9.
答:这个多边形是九边形.
方法二:设这个多边形的边数为 n ,根据题意得
解得 n = 9.
答:这个多边形是九边形.
4.一个多边形的外角和是内角和的 ,求这个多边形
的边数.
解:设多边形的边数为 n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于 360°,
∴ (n-2) 180°= 5×360°.
解得 n = 12.
∴这个多边形的边数为 12.
5. 如图,在正五边形 ABCDE 中,连接 BE,求∠BED 的度数.
解:由题意得
AB = AE,
所以∠AEB = ( 180°- ∠A ) = 36°,
所以∠BED = ∠AED - ∠AEB = 108°- 36°= 72°.
6. 一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.
解:设该正多边形的内角是 x°,外角是 y°,
则得到一个方程组 解得
而任何多边形的外角和是 360°,
则该正多边形的边数为 360÷120 = 3.
故这个多边形的每个内角的度数是 60°,边数是3.
小结
多边形的外角与外角和
外角和
多边形的外角和等于360°
特别注意:多边形的外角和与边数无关
四边形
具有不稳定性
外角的定义
第2章 四边形
2.1 多边形
第2课时 多边形的外角和
课时导入
动脑筋
我们已经知道三角形的外角和为360°,那么四边形的外角和为多少度呢?
首先我们来了解几个概念:
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. 如图所示.
在多边形的每个顶点处取一个外角,它们的和叫做多边形的外角和.
如图,在五边形的每个顶点处各取一个外角.
问题1 任意一个外角和它相邻的内角有什么关系?
问题2 五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°= 900°
E
B
C
D
1
2
3
4
5
A
五边形的外角和
= 360°
= 5个平角和
-五边形内角和
= 5×180°
-(5-2) × 180°
结论:五边形的外角和等于 360°.
问题3 这五个平角和与五边形的内角和、外角和有什
么关系?
n 边形外角和
n 边形的外角和等于 360°.
-(n-2) × 180°
= 360°
= n 个平角和- n 边形内角和
= n×180°
An
A2
A3
A4
1
2
3
4
n
A1
n 边形的外角和又是多少呢?
与边数无关
思考
问题4 回想正多边形的性质,你知道正 n 边形的每个
内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
任意多边形的外角和等于360°.
知识讲解
多边形的外角和:
n边形的外角和与边数没有关系.
例
一个多边形的内角和等于它外角和的 5 倍,它是几边形?
解: 设多边形的边数为 n,
则它的内角和等于 (n -2)·180°.
由题意得
(n - 2)·180°= 5×360°,
解得 n = 12.
因此这个多边形是十二边形.
观察
三角形具有稳定性,那么四边形呢?
四边形具有不稳定性:
各边的长确定后,图形形状不能确定.
在实际生活中,我们经常利用四边形的不稳定性,例如图1,2中的电动伸缩门. 有时又要克服四边形的不稳定性,例如在图3中的栅栏两横梁之间加钉斜木条,构成三角形,这是利用了三角形的稳定性.
图1
图2
图3
随 堂 小 测
1. 一个正多边形的内角 135°,则这个正多边形的边数为______.
8
2. 如图所示,小明从点 A 出发,沿直线前进 10 米后左转 24°,再沿直线前进 10 米,又向左转 24°……照这样走下去,他第一次回到出发地点 A 时,走的路程一共是________米.
150
3.已知一个多边形的每个内角与外角的比都是 7∶2,求这个多边形的边数.
方法一:设这个多边形的内角为 7x°,外角为 2x°,
根据题意得
7x + 2x = 180,
解得 x = 20.
即每个内角是 140°,每个外角是 40°.
360°÷40° = 9.
答:这个多边形是九边形.
方法二:设这个多边形的边数为 n ,根据题意得
解得 n = 9.
答:这个多边形是九边形.
4.一个多边形的外角和是内角和的 ,求这个多边形
的边数.
解:设多边形的边数为 n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于 360°,
∴ (n-2) 180°= 5×360°.
解得 n = 12.
∴这个多边形的边数为 12.
5. 如图,在正五边形 ABCDE 中,连接 BE,求∠BED 的度数.
解:由题意得
AB = AE,
所以∠AEB = ( 180°- ∠A ) = 36°,
所以∠BED = ∠AED - ∠AEB = 108°- 36°= 72°.
6. 一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.
解:设该正多边形的内角是 x°,外角是 y°,
则得到一个方程组 解得
而任何多边形的外角和是 360°,
则该正多边形的边数为 360÷120 = 3.
故这个多边形的每个内角的度数是 60°,边数是3.
小结
多边形的外角与外角和
外角和
多边形的外角和等于360°
特别注意:多边形的外角和与边数无关
四边形
具有不稳定性
外角的定义
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
