2.2.1 第2课时 平行四边形对角线的性质 课件(共18张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 2.2.1 第2课时 平行四边形对角线的性质 课件(共18张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 203.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第2章 四边形
2.2 平行四边形
第2课时 平行四边形对角线的性质
2.2.1 平行四边形的性质
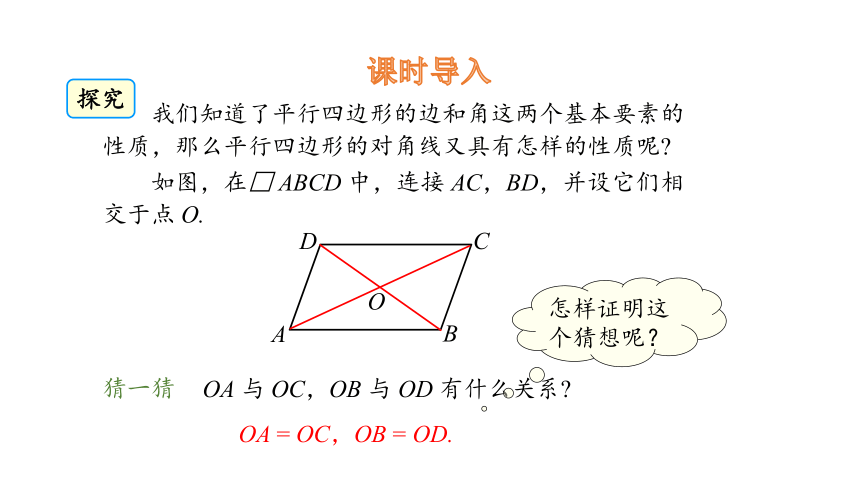
课时导入
我们知道了平行四边形的边和角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢
如图,在□ ABCD 中,连接 AC,BD,并设它们相交于点 O.
OA 与 OC,OB 与 OD 有什么关系
猜一猜
OA = OC,OB = OD.
怎样证明这个猜想呢?
A
B
C
D
O
探究
已知:如图,□ABCD 的对角线 AC、BD 相交于点 O.
求证:OA = OC,OB = OD.
证明:
∵四边形 ABCD 是平行四边形,
∴ AD = BC,AD∥BC.
∴ ∠1 = ∠2,∠3 = ∠4.
∴ △AOD≌△COB(ASA).
∴ OA = OC,OB = OD.
A
C
D
B
O
3
2
4
1
证明猜想
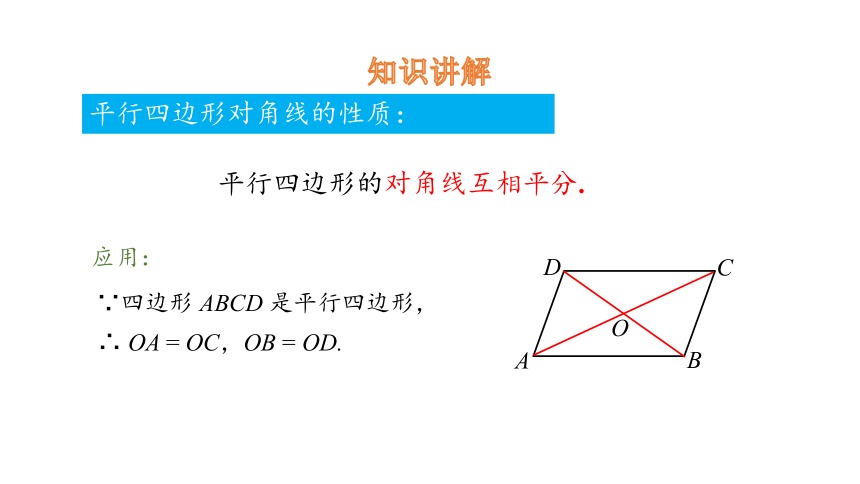
知识讲解
平行四边形对角线的性质:
平行四边形的对角线互相平分.
应用:
∵四边形 ABCD 是平行四边形,
∴ OA = OC,OB = OD.
A
B
C
D
O
例1
已知 ABCD 的周长为 60 cm,对角线 AC、BD 相交于点 O,△AOB 的周长比 △DOA 的周长长 5 cm,求这个平行四边形各边的长.
解:∵四边形 ABCD 是平行四边形,
∴OB = OD,AB = CD,AD = BC.
∵△AOB 的周长比△DOA 的周长长 5 cm,
∴ AB-AD = 5 cm.
又∵ ABCD 的周长为 60 cm,∴ AB+AD=30 cm,
则 AB = CD = 17.5 cm,AD = BC = 12.5 cm.
归纳:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
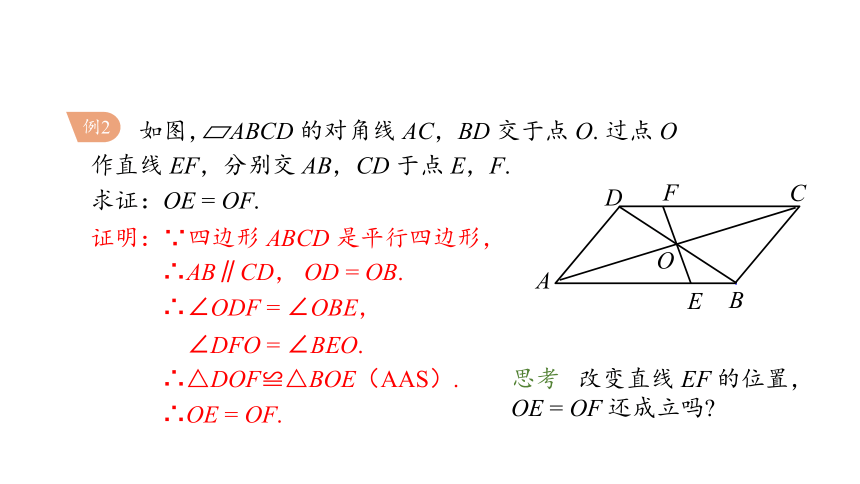
例2
如图, ABCD 的对角线 AC,BD 交于点 O. 过点 O 作直线 EF,分别交 AB,CD 于点 E,F.
求证:OE = OF.
A
B
C
D
F
E
O
证明:∵四边形 ABCD 是平行四边形,
∴∠ODF = ∠OBE,
∠DFO = ∠BEO.
∴△DOF≌△BOE(AAS).
∴AB∥CD, OD = OB.
∴OE = OF.
思考 改变直线 EF 的位置,OE = OF 还成立吗
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
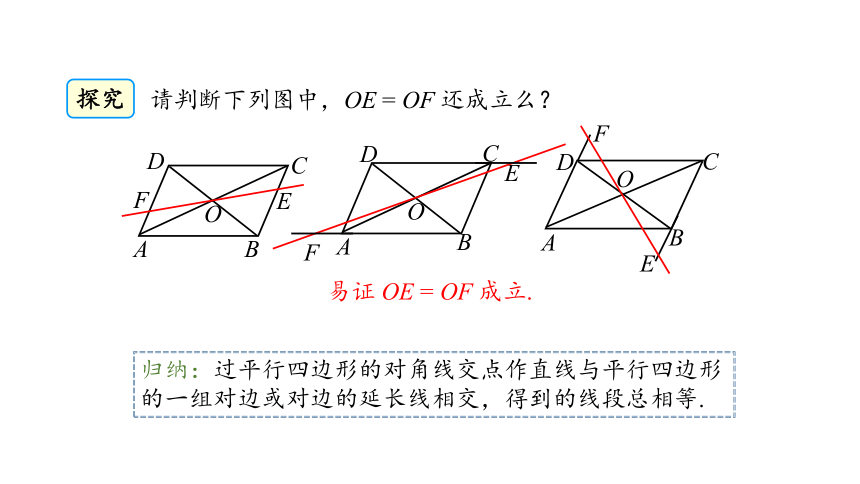
请判断下列图中,OE = OF 还成立么?
易证 OE = OF 成立.
归纳:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
探究
例3
解:设 AB = x,则 BC = 24 - x.
根据平行四边形的面积公式可得
5x = 10 ( 24 - x ),
解得 x = 16.
则平行四边形 ABCD 的面积为 5×16 = 80.
如图,平行四边形 ABCD 中,DE⊥AB 于 E,DF⊥BC 于 F,若平行四边形 ABCD 的周长为 48,DE = 5,DF = 10,求平行四边形 ABCD 的面积.
归纳:已知平行四边形的高 DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
问题 平行四边形的对角线分平行四边形 ABCD 为四个三角形,它们的面积有怎样的关系呢?
解:相等. 理由如下:
∵四边形 ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵△ADO 与△ODC 等底同高,
∴S△ADO=S△ODC.
同理可得 S△ADO=S△ODC=S△BCO=S△AOB.
归纳:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
随 堂 小 测
1. 在□ABCD中,AC = 24,BD = 38,AB = m,则 m 的取值范围是 ( )
A. 24<m<39 B. 14<m<62
C. 7<m<31 D. 7<m<12
B
C
D
A
O
C
2. 如图, ABCD的对角线 AC,BD 相交于 O,EF 过点 O 与 AD,BC 分别相交于 E,F,若 AB = 4,BC = 5,OE = 1.5,那么四边形 EFCD 的周长为( )
A. 16 B. 14 C. 12 D. 10
A
D
C
B
F
E
O
C
3. 如图,平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,AB⊥AC,AB = 3,AD = 5,
则 BD 的长是 .
A
D
C
B
O
4. 如图,平行四边形 ABCD 的面积为 20,对角线 AC,BD 相交于点 O,点 E,F 分别是 AB,CD 上的点,且 AE = DF,则图中阴影部分的面积为_______.
5
5. 如图,在平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,平行四边形 ABCD 的周长是 100 cm,△AOB 与 △BOC 的周长的和是 122 cm,且 AC∶DB = 2∶1,求 AC 和 BD 的长.
解:∵四边形 ABCD 是平行四边形,
∴ AD = BC,AB = CD,OB = OD,
∴ AB + BC = 50.
∵△AOB 与△BOC 的周长的和是 122 cm,
∴OA + OB + AB + OB + OC + BC = 122,
即 AC + BD = 122 - 50 = 72.
又∵AC∶DB = 2∶1,
∴AC = 48 cm,BD = 24 cm.
6.如图,平行四边形 ABCD 中,AC,BD 交于 O 点,点 E,F 分别是 AO,CO 的中点,试判断线段 BE,DF 的关系并证明你的结论.
解:BE = DF,BE∥DF.
理由如下:∵四边形 ABCD 是平行四边形,
∴OA = OC,OB = OD.
∵点 E,F 分别是 AO,CO 的中点,
∴OE = OF.
在 △OFD 和 △OEB 中,
OF = OE,∠DOF = ∠BOE,OD = OB,
∴△OFD≌△OEB (SAS).
∴∠OEB=∠OFD,BE=DF. ∴BE∥DF.
A
B
C
D
O
解:∵四边形 ABCD 是平行四边形,
根据勾股定理得
∴ BC = AD = 8,CD = AB = 10.
∴△ABC 是直角三角形.
又∵OA = OC,
7. 如图,在 ABCD 中,AB = 10,AD = 8,AC⊥BC. 求 BC,CD,AC,OA 的长,以及 ABCD的面积.
∵AC ⊥ BC,
小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的平行线段相等
两条平行线间的距离
两组对角分别相等,邻角互补
小结
平行四边形对角线的性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分,且与对角线围成的三角形相对的两个全等
第2章 四边形
2.2 平行四边形
第2课时 平行四边形对角线的性质
2.2.1 平行四边形的性质
课时导入
我们知道了平行四边形的边和角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢
如图,在□ ABCD 中,连接 AC,BD,并设它们相交于点 O.
OA 与 OC,OB 与 OD 有什么关系
猜一猜
OA = OC,OB = OD.
怎样证明这个猜想呢?
A
B
C
D
O
探究
已知:如图,□ABCD 的对角线 AC、BD 相交于点 O.
求证:OA = OC,OB = OD.
证明:
∵四边形 ABCD 是平行四边形,
∴ AD = BC,AD∥BC.
∴ ∠1 = ∠2,∠3 = ∠4.
∴ △AOD≌△COB(ASA).
∴ OA = OC,OB = OD.
A
C
D
B
O
3
2
4
1
证明猜想
知识讲解
平行四边形对角线的性质:
平行四边形的对角线互相平分.
应用:
∵四边形 ABCD 是平行四边形,
∴ OA = OC,OB = OD.
A
B
C
D
O
例1
已知 ABCD 的周长为 60 cm,对角线 AC、BD 相交于点 O,△AOB 的周长比 △DOA 的周长长 5 cm,求这个平行四边形各边的长.
解:∵四边形 ABCD 是平行四边形,
∴OB = OD,AB = CD,AD = BC.
∵△AOB 的周长比△DOA 的周长长 5 cm,
∴ AB-AD = 5 cm.
又∵ ABCD 的周长为 60 cm,∴ AB+AD=30 cm,
则 AB = CD = 17.5 cm,AD = BC = 12.5 cm.
归纳:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
例2
如图, ABCD 的对角线 AC,BD 交于点 O. 过点 O 作直线 EF,分别交 AB,CD 于点 E,F.
求证:OE = OF.
A
B
C
D
F
E
O
证明:∵四边形 ABCD 是平行四边形,
∴∠ODF = ∠OBE,
∠DFO = ∠BEO.
∴△DOF≌△BOE(AAS).
∴AB∥CD, OD = OB.
∴OE = OF.
思考 改变直线 EF 的位置,OE = OF 还成立吗
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
请判断下列图中,OE = OF 还成立么?
易证 OE = OF 成立.
归纳:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
探究
例3
解:设 AB = x,则 BC = 24 - x.
根据平行四边形的面积公式可得
5x = 10 ( 24 - x ),
解得 x = 16.
则平行四边形 ABCD 的面积为 5×16 = 80.
如图,平行四边形 ABCD 中,DE⊥AB 于 E,DF⊥BC 于 F,若平行四边形 ABCD 的周长为 48,DE = 5,DF = 10,求平行四边形 ABCD 的面积.
归纳:已知平行四边形的高 DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
问题 平行四边形的对角线分平行四边形 ABCD 为四个三角形,它们的面积有怎样的关系呢?
解:相等. 理由如下:
∵四边形 ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵△ADO 与△ODC 等底同高,
∴S△ADO=S△ODC.
同理可得 S△ADO=S△ODC=S△BCO=S△AOB.
归纳:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
随 堂 小 测
1. 在□ABCD中,AC = 24,BD = 38,AB = m,则 m 的取值范围是 ( )
A. 24<m<39 B. 14<m<62
C. 7<m<31 D. 7<m<12
B
C
D
A
O
C
2. 如图, ABCD的对角线 AC,BD 相交于 O,EF 过点 O 与 AD,BC 分别相交于 E,F,若 AB = 4,BC = 5,OE = 1.5,那么四边形 EFCD 的周长为( )
A. 16 B. 14 C. 12 D. 10
A
D
C
B
F
E
O
C
3. 如图,平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,AB⊥AC,AB = 3,AD = 5,
则 BD 的长是 .
A
D
C
B
O
4. 如图,平行四边形 ABCD 的面积为 20,对角线 AC,BD 相交于点 O,点 E,F 分别是 AB,CD 上的点,且 AE = DF,则图中阴影部分的面积为_______.
5
5. 如图,在平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,平行四边形 ABCD 的周长是 100 cm,△AOB 与 △BOC 的周长的和是 122 cm,且 AC∶DB = 2∶1,求 AC 和 BD 的长.
解:∵四边形 ABCD 是平行四边形,
∴ AD = BC,AB = CD,OB = OD,
∴ AB + BC = 50.
∵△AOB 与△BOC 的周长的和是 122 cm,
∴OA + OB + AB + OB + OC + BC = 122,
即 AC + BD = 122 - 50 = 72.
又∵AC∶DB = 2∶1,
∴AC = 48 cm,BD = 24 cm.
6.如图,平行四边形 ABCD 中,AC,BD 交于 O 点,点 E,F 分别是 AO,CO 的中点,试判断线段 BE,DF 的关系并证明你的结论.
解:BE = DF,BE∥DF.
理由如下:∵四边形 ABCD 是平行四边形,
∴OA = OC,OB = OD.
∵点 E,F 分别是 AO,CO 的中点,
∴OE = OF.
在 △OFD 和 △OEB 中,
OF = OE,∠DOF = ∠BOE,OD = OB,
∴△OFD≌△OEB (SAS).
∴∠OEB=∠OFD,BE=DF. ∴BE∥DF.
A
B
C
D
O
解:∵四边形 ABCD 是平行四边形,
根据勾股定理得
∴ BC = AD = 8,CD = AB = 10.
∴△ABC 是直角三角形.
又∵OA = OC,
7. 如图,在 ABCD 中,AB = 10,AD = 8,AC⊥BC. 求 BC,CD,AC,OA 的长,以及 ABCD的面积.
∵AC ⊥ BC,
小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的平行线段相等
两条平行线间的距离
两组对角分别相等,邻角互补
小结
平行四边形对角线的性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分,且与对角线围成的三角形相对的两个全等
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
