2.2.2 第1课时 平行四边形的判定定理1、2 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 2.2.2 第1课时 平行四边形的判定定理1、2 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 670.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
第2章 四边形
2.2 平行四边形
第1课时 平行四边形的判定定理1、2
2.2.2 平行四边形的判定
学习目标
1.探索并证明平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
2.会运用平行四边形的判定定理判定一个四边形是否为平行四边形.
课时导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
只要使互相平行的夹在铁轨之间的枕木长相等就可以了
这是为什么呢?
问题 我们知道,两组对边分别平行的四边形是平行四边形. 如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想 1:一组对边相等的四边形是平行四边形.
等腰梯形不是平行四边形,因而此猜想错误.
猜想 2:一组对边平行的四边形是平行四边形.
梯形的上、下底平行,但不是平行四边形,因而此猜想错误.
动脑筋
B
A
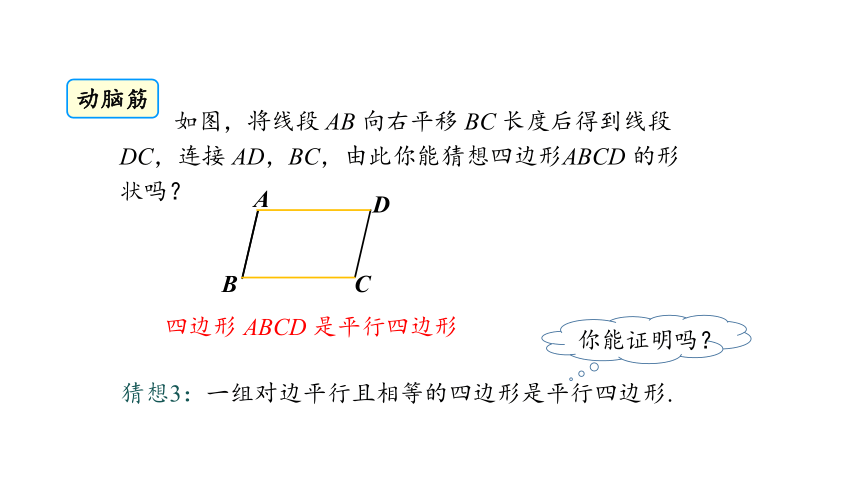
如图,将线段 AB 向右平移 BC 长度后得到线段 DC,连接 AD,BC,由此你能猜想四边形ABCD 的形状吗?
D
C
四边形 ABCD 是平行四边形
猜想3:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
证明猜想
A
B
C
D
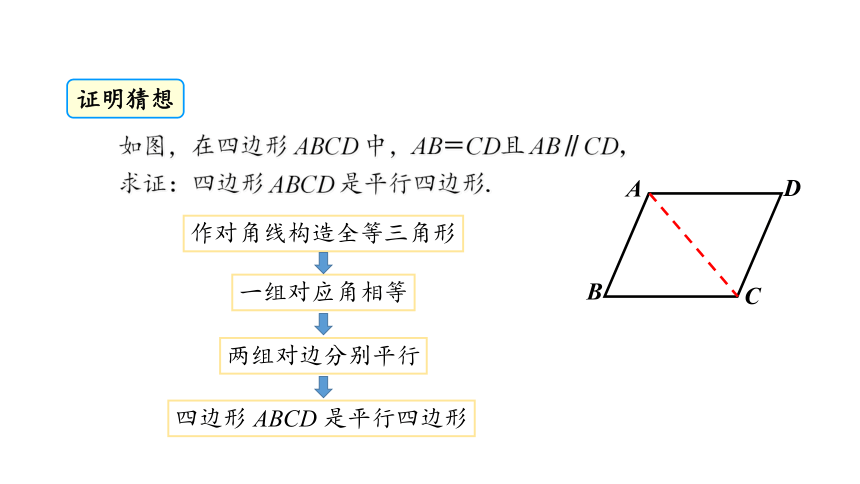
作对角线构造全等三角形
一组对应角相等
两组对边分别平行
四边形 ABCD 是平行四边形
如图,在四边形 ABCD 中,AB=CD且 AB∥CD,
求证:四边形 ABCD 是平行四边形.
A
B
C
D
2
1
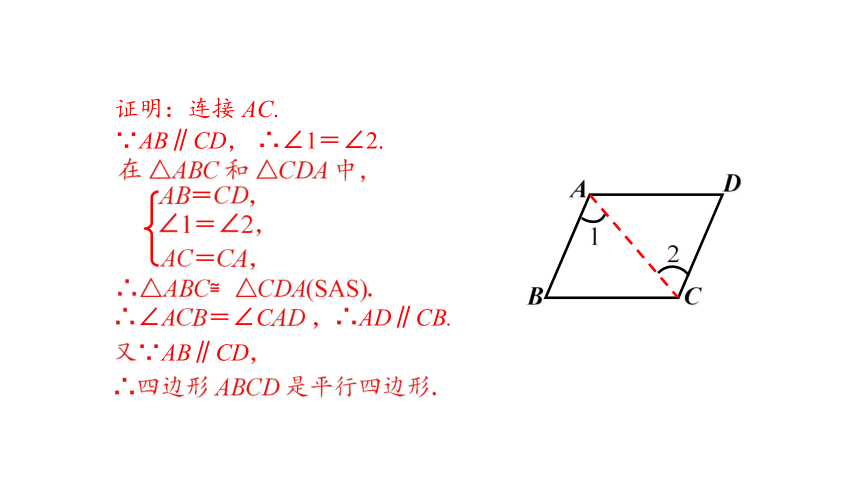
证明:连接 AC.
∵AB∥CD, ∴∠1=∠2.
在 △ABC 和 △CDA 中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS).
∴∠ACB=∠CAD ,∴AD∥CB.
又∵AB∥CD,
∴四边形 ABCD 是平行四边形.
知识讲解
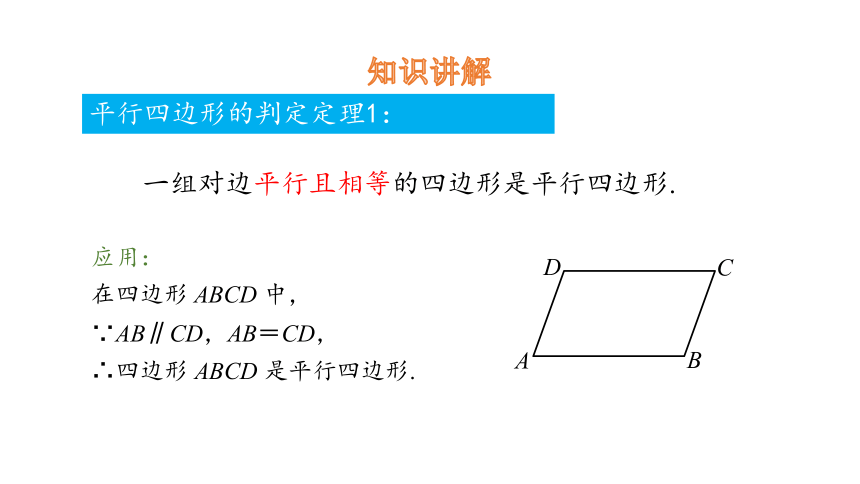
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
应用:
A
B
C
D
在四边形 ABCD 中,
∵AB∥CD,AB=CD,
∴四边形 ABCD 是平行四边形.
例1
证明:∵四边形 ABCD 是平行四边形,
∴AB=CD,EB∥FD.
又∵EB = AB ,FD= CD,
∴EB=FD .
∴四边形 EBFD 是平行四边形.
如图 ,在平行四边形 ABCD 中,E,F 分别是AB,CD 的中点. 求证:四边形 EBFD 是平行四边形.
问题1:将两长两短的四根细木条用小钉固定在一起,任意拉动,所得的四边形是平行四边形吗
动脑筋
猜想:两组对边分别相等的四边形是平行四边形.
问题2:用两支同样长的铅笔和两支同样长的钢笔能摆成一个平行四边形吗
证明猜想
你能根据平行四边形的定义证明吗?
已知:四边形 ABCD 中,AB=DC,AD=BC.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
连接 AC.
在 △ABC 和 △CDA 中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS).
∴ ∠1=∠4,∠ 2=∠3.
∴ AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
知识讲解
平行四边形的判定定理2:
两组对边分别相等的四边形是平行四边形.
应用:
A
B
C
D
在四边形 ABCD 中,
∵AB=CD,AD=BC,
∴四边形 ABCD 是平行四边形.
例2
如图, AD⊥AC,BC⊥AC,且 AB = CD,求证:四边形 ABCD 是平行四边形.
证明:在 Rt△ABC 和 Rt△CDA 中,
∵AC = CA,AB = CD,
∴Rt△ABC≌Rt△CDA(HL).
∴BC = DA.
又∵AB = CD,
∴四边形 ABCD 是平行四边形.
随 堂 小 测
1. 已知四边形 ABCD 中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形 ABCD 成为平行四边形的选法是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
2.如图所示,△ABC 是等边三角形,P 是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC 的周长为 24,则 PD + PE + PF = .
A
F
B
D
C
E
P
8
3.已知 AD∥BC ,要使这个四边形 ABCD 为平行四边形,需要增加条件 .
AD = BC 或 AB∥CD
4. 如图,点 A,B,C,D 在同一条直线上,点 E, F 分别在直线 AD 的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形 BFCE 是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即 AC=BD.
在 △ACE 和 △DBF 中,
AC=DB ,∠A=∠D, AE=DF,
∴△ACE≌△DBF(SAS).
∴CE=BF,∠ACE=∠DBF.
∴CE∥BF.
∴四边形 BFCE 是平行四边形.
证明:∵四边形 AEFD 和 EBCF 都是平行四边形,
∴AD∥EF,AD = EF,
EF∥BC, EF = BC.
∴AD∥BC,AD = BC.
∴四边形 ABCD 是平行四边形.
A
B
C
D
E
F
5. 四边形 AEFD 和 EBCF 都是平行四边形,求证:
四边形 ABCD 是平行四边形.
证明:在平行四边形 ABCD 中,∠A = ∠C,AD = BC,
又∵BF = DH,
∴AH = CF.
又∵AE = CG,
∴△AEH≌△CGF(SAS).
∴EH = GF.
同理得△BEF≌△DGH(SAS)∴GH = EF.
∴四边形 EFGH 是平行四边形.
6. 如图,已知 E,F,G,H 分别是 ABCD 的边 AB,BC,CD,DA 上的点,且 AE = CG,BF = DH.求证:四边形 EFGH 是平行四边形.
7. 如图,点 C 是 AB 的中点,AD=CE,CD=BE.
(1)求证:△ACD ≌△CBE;
(2)连接 DE,求证:四边形 CBED 是平行四边形.
证明:(1)∵点 C 是 AB 的中点,∴AC=BC.
在 △ADC 与 △CEB 中,
AD=CE ,CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS).
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE. ∴CD∥BE.
又∵CD=BE,∴四边形 CBED 是平行四边形.
小结
平行四边形的判定
判定定理1
判定定理2
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
第2章 四边形
2.2 平行四边形
第1课时 平行四边形的判定定理1、2
2.2.2 平行四边形的判定
学习目标
1.探索并证明平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
2.会运用平行四边形的判定定理判定一个四边形是否为平行四边形.
课时导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
只要使互相平行的夹在铁轨之间的枕木长相等就可以了
这是为什么呢?
问题 我们知道,两组对边分别平行的四边形是平行四边形. 如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想 1:一组对边相等的四边形是平行四边形.
等腰梯形不是平行四边形,因而此猜想错误.
猜想 2:一组对边平行的四边形是平行四边形.
梯形的上、下底平行,但不是平行四边形,因而此猜想错误.
动脑筋
B
A
如图,将线段 AB 向右平移 BC 长度后得到线段 DC,连接 AD,BC,由此你能猜想四边形ABCD 的形状吗?
D
C
四边形 ABCD 是平行四边形
猜想3:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
证明猜想
A
B
C
D
作对角线构造全等三角形
一组对应角相等
两组对边分别平行
四边形 ABCD 是平行四边形
如图,在四边形 ABCD 中,AB=CD且 AB∥CD,
求证:四边形 ABCD 是平行四边形.
A
B
C
D
2
1
证明:连接 AC.
∵AB∥CD, ∴∠1=∠2.
在 △ABC 和 △CDA 中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS).
∴∠ACB=∠CAD ,∴AD∥CB.
又∵AB∥CD,
∴四边形 ABCD 是平行四边形.
知识讲解
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
应用:
A
B
C
D
在四边形 ABCD 中,
∵AB∥CD,AB=CD,
∴四边形 ABCD 是平行四边形.
例1
证明:∵四边形 ABCD 是平行四边形,
∴AB=CD,EB∥FD.
又∵EB = AB ,FD= CD,
∴EB=FD .
∴四边形 EBFD 是平行四边形.
如图 ,在平行四边形 ABCD 中,E,F 分别是AB,CD 的中点. 求证:四边形 EBFD 是平行四边形.
问题1:将两长两短的四根细木条用小钉固定在一起,任意拉动,所得的四边形是平行四边形吗
动脑筋
猜想:两组对边分别相等的四边形是平行四边形.
问题2:用两支同样长的铅笔和两支同样长的钢笔能摆成一个平行四边形吗
证明猜想
你能根据平行四边形的定义证明吗?
已知:四边形 ABCD 中,AB=DC,AD=BC.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
连接 AC.
在 △ABC 和 △CDA 中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS).
∴ ∠1=∠4,∠ 2=∠3.
∴ AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
知识讲解
平行四边形的判定定理2:
两组对边分别相等的四边形是平行四边形.
应用:
A
B
C
D
在四边形 ABCD 中,
∵AB=CD,AD=BC,
∴四边形 ABCD 是平行四边形.
例2
如图, AD⊥AC,BC⊥AC,且 AB = CD,求证:四边形 ABCD 是平行四边形.
证明:在 Rt△ABC 和 Rt△CDA 中,
∵AC = CA,AB = CD,
∴Rt△ABC≌Rt△CDA(HL).
∴BC = DA.
又∵AB = CD,
∴四边形 ABCD 是平行四边形.
随 堂 小 测
1. 已知四边形 ABCD 中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形 ABCD 成为平行四边形的选法是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
2.如图所示,△ABC 是等边三角形,P 是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC 的周长为 24,则 PD + PE + PF = .
A
F
B
D
C
E
P
8
3.已知 AD∥BC ,要使这个四边形 ABCD 为平行四边形,需要增加条件 .
AD = BC 或 AB∥CD
4. 如图,点 A,B,C,D 在同一条直线上,点 E, F 分别在直线 AD 的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形 BFCE 是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即 AC=BD.
在 △ACE 和 △DBF 中,
AC=DB ,∠A=∠D, AE=DF,
∴△ACE≌△DBF(SAS).
∴CE=BF,∠ACE=∠DBF.
∴CE∥BF.
∴四边形 BFCE 是平行四边形.
证明:∵四边形 AEFD 和 EBCF 都是平行四边形,
∴AD∥EF,AD = EF,
EF∥BC, EF = BC.
∴AD∥BC,AD = BC.
∴四边形 ABCD 是平行四边形.
A
B
C
D
E
F
5. 四边形 AEFD 和 EBCF 都是平行四边形,求证:
四边形 ABCD 是平行四边形.
证明:在平行四边形 ABCD 中,∠A = ∠C,AD = BC,
又∵BF = DH,
∴AH = CF.
又∵AE = CG,
∴△AEH≌△CGF(SAS).
∴EH = GF.
同理得△BEF≌△DGH(SAS)∴GH = EF.
∴四边形 EFGH 是平行四边形.
6. 如图,已知 E,F,G,H 分别是 ABCD 的边 AB,BC,CD,DA 上的点,且 AE = CG,BF = DH.求证:四边形 EFGH 是平行四边形.
7. 如图,点 C 是 AB 的中点,AD=CE,CD=BE.
(1)求证:△ACD ≌△CBE;
(2)连接 DE,求证:四边形 CBED 是平行四边形.
证明:(1)∵点 C 是 AB 的中点,∴AC=BC.
在 △ADC 与 △CEB 中,
AD=CE ,CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS).
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE. ∴CD∥BE.
又∵CD=BE,∴四边形 CBED 是平行四边形.
小结
平行四边形的判定
判定定理1
判定定理2
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
