2.4 三角形的中位线 课件(共22张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 2.4 三角形的中位线 课件(共22张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 292.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
第2章 四边形
2.4 三角形的中位线
学习目标
1.了解三角形中位线的概念.
2.探索并证明三角形的中位线定理.
3.会运用三角形的中位线定理进行简单的推理与计算.
学习重点、难点
三角形的中位线定理及其应用.
重点:
难点:
三角形的中位线定理的探索与证明.
课时导入
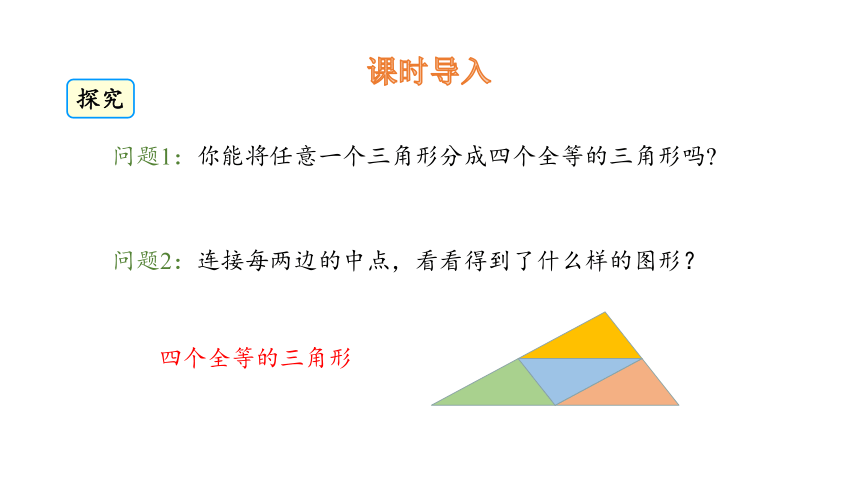
问题1:你能将任意一个三角形分成四个全等的三角形吗
问题2:连接每两边的中点,看看得到了什么样的图形?
四个全等的三角形
探究
知识讲解
三角形中位线的概念:
连接三角形两边中点的线段叫作三角形的中位线.
D
A
B
C
E
② 如果 DE 为△ABC 的中位线,那么 D、E 分别为 AB、AC 的 .
① 如果 D、E 分别为 AB、AC 的中点,那么 DE 为△ABC 的 ;
中位线
中点
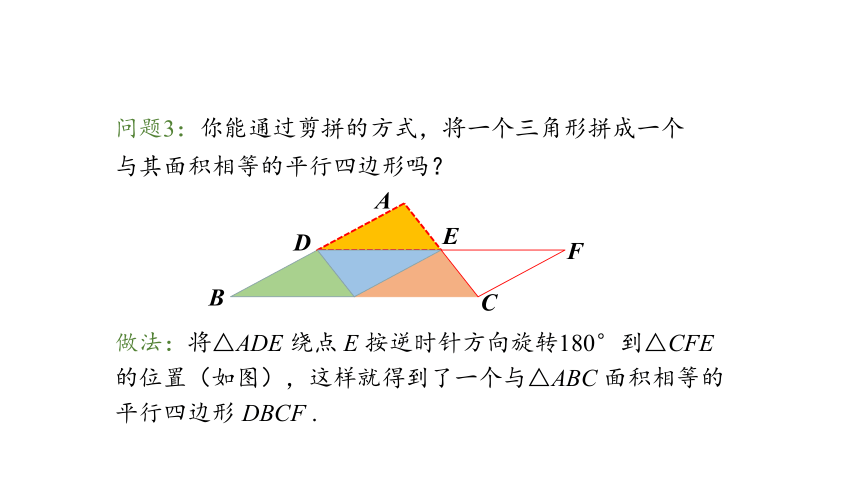
问题3:你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
做法:将△ADE 绕点 E 按逆时针方向旋转180°到△CFE 的位置(如图),这样就得到了一个与△ABC 面积相等的平行四边形 DBCF .
A
D
E
F
C
B
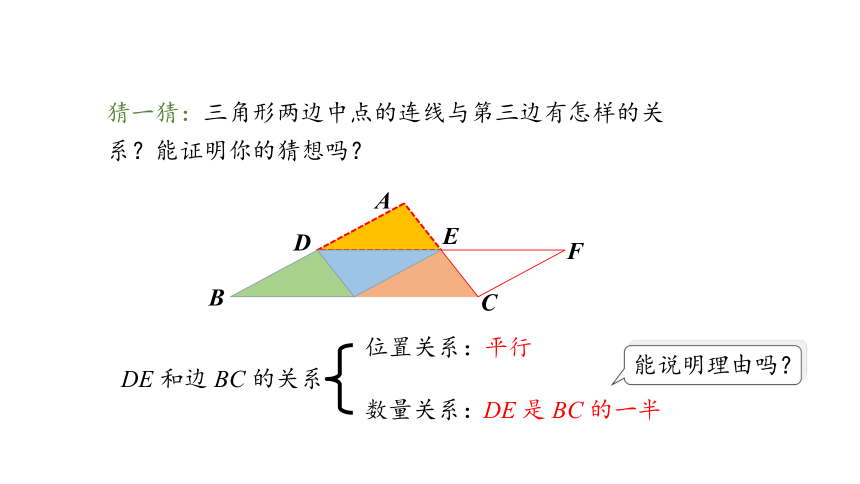
猜一猜:三角形两边中点的连线与第三边有怎样的关系?能证明你的猜想吗?
DE 和边 BC 的关系
数量关系:
位置关系:
平行
DE 是 BC 的一半
A
D
E
F
C
B
能说明理由吗?
已知:如图,在△ABC 中,DE 是 △ABC 的中位线. 求证:
DE∥BC,
DE = BC.
E
A
B
C
D
F
证明:如图,延长 DE 至 F,使 EF = DE,连接 CF.
∵ AE = CE, ∠AED = ∠CEF,
∴△ADE≌△CFE.
∴AD = CF,∠A = ∠ECF.
∴CF∥AB.
∵AD = BD,
∴四边形 DBCF 是平行四边形.
∴BD = CF.
证明猜想
∴DE∥BC,
知识讲解
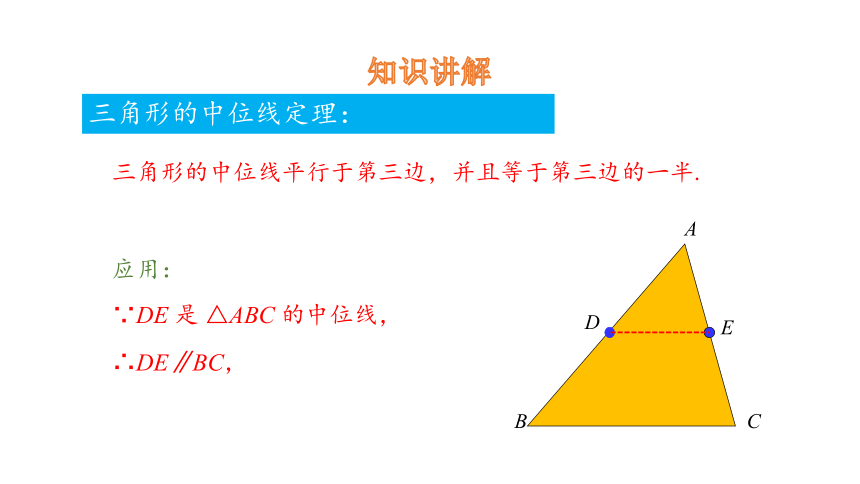
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
D
A
B
C
E
应用:
∵DE 是 △ABC 的中位线,
∴DE∥BC,
(1) 当在三角形或几何图形中看到中点,尤其是两个或者两个以上的中点时可以联想到三角形的中位线定理.
(2) 三角形的中位线定理既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),所以在解决相关问题时要两方面结合起来灵活应用.
归纳:
已知:如图,在四边形 ABCD 中, E,F,G,H 分别为各边的中点. 求证:四边形 EFGH 是平行四边形.
分析:将四边形 ABCD 分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.
A
B
C
D
E
F
G
H
例
证明:连接 AC.
∵E,F,G,H 分别为各边的中点,
∴ EF∥HG,EF = HG.
∴EF∥AC,
HG∥AC,
∴四边形 EFGH 是平行四边形.
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
不变化
四边形 EFGH 的形状和什么有关?
想一想:若平行四边形 ABCD 变成任意的四边形,其它条件不变,则四边形 EFGH 的形状会变化吗?为什么?
随 堂 小 测
1. 如图,MN 为△ABC 的中位线,若∠ABC = 61°,则∠AMN = °,若 MN = 12 ,则 BC = .
A
M
B
C
N
61
24
A
D
B
C
E
2. 如图,△ABC 中,D ,E 分别为 AB,AC 的中点,当 BC = 10 cm时,则 DE = cm.
5
第1题图
第2题图
3. 已知:三角形的各边分别为 6 cm,8 cm,12 cm,则连接各边中点所成三角形的周长为 ____ cm.
13
4. 已知:三角形的周长为 64 cm,则连接各边中点所成三角形的周长为 ____cm.
32
5. 如图,已知△ABC 中,AB = 3 cm,BC = 3.4 cm,AC = 4 cm 且 D,E,F 分别为 AC,AB,BC 边的中点,则△DEF 的周长是 cm.
A
B
C
D
E
F
5.2
6. 在△ABC 中,中线 CE、BF 相交点 O,M、N 分别是 OB、OC 的中点,则 EF 和 MN 的关系是_______________.
平行且相等
7. A,B 两村相隔一座大山,你能想办法测出 A,B 两村的直线距离 AB 的大小吗?若 MN = 360 m,则 AB = m.
A
B
C
M
N
解析:在 AB 外选一点 C,使 C 能直接到达 A 和 B,连接 AC 和 BC,并分别找出 AC 和 BC 的中点 M、N,测出 MN 的长,就可知 A、B 两点的距离.
720
如果,M、N 两点之间还有阻隔,你有什么解决办法?
两次利用中位线,分别取 CM 和 CN 的中点.
8. 如图,在 Rt△ABC 中,∠C = 90°, D 是斜边 AB 的中点,E 是 BC 的中点.
(2)若 AB = 10,DE = 4, 求△ABC 的面积.
(1)DE⊥BC 吗?为什么?
A
B
C
D
E
∴DE∥BC.
解:∵DE = 4,∴AC = 8.
∵AB = 10,AC = 8,∴BC = 6.
解:∵D、E 分别是 AB、BC 的中点,
∵∠C = 90°,∴∠DEC = 90°. ∴DE⊥BC.
9. 规律探究:(1)△ABC 的周长为 a,
D、E、F分别为△ABC各边中点,△DEF的周长为 ;
G、H、I分别为△DEF各边中点,△GHI的周长为 ;
C
A
B
D
F
E
G
H
I
像这样下去,第 3 个三角形的周长为 ;
第 n 个三角形的周长为 .
你发现了什么?
,…,
(2)已知:△ABC 的面积为 S ,连接各边中点得△A1B1C1,再连接△A1B1C1 各边中点得△A2B2C2 ,…,
则第 1 次连接所得△A1B1C1 面积=____;
第 2 次连接所得△A2B2C2 面积= ;
第 3 次连接所得△A3B3C3 面积= ;
,…,
第 n 次连接所得△AnBnCn 面积= .
A
C
A1
B1
C1
A2
B2
C2
B
C3
A3
B3
次数 1 2 3 … n
所得三角形周长 …
所得三角形面积 …
通过上述题目我们可以得到:
小结
三角形中位线
定 义
连接三角形两边中点的线段叫作三角形的中位线
定 理
三角形的中位线平行于第三边,并且等于第三边的一半
第2章 四边形
2.4 三角形的中位线
学习目标
1.了解三角形中位线的概念.
2.探索并证明三角形的中位线定理.
3.会运用三角形的中位线定理进行简单的推理与计算.
学习重点、难点
三角形的中位线定理及其应用.
重点:
难点:
三角形的中位线定理的探索与证明.
课时导入
问题1:你能将任意一个三角形分成四个全等的三角形吗
问题2:连接每两边的中点,看看得到了什么样的图形?
四个全等的三角形
探究
知识讲解
三角形中位线的概念:
连接三角形两边中点的线段叫作三角形的中位线.
D
A
B
C
E
② 如果 DE 为△ABC 的中位线,那么 D、E 分别为 AB、AC 的 .
① 如果 D、E 分别为 AB、AC 的中点,那么 DE 为△ABC 的 ;
中位线
中点
问题3:你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
做法:将△ADE 绕点 E 按逆时针方向旋转180°到△CFE 的位置(如图),这样就得到了一个与△ABC 面积相等的平行四边形 DBCF .
A
D
E
F
C
B
猜一猜:三角形两边中点的连线与第三边有怎样的关系?能证明你的猜想吗?
DE 和边 BC 的关系
数量关系:
位置关系:
平行
DE 是 BC 的一半
A
D
E
F
C
B
能说明理由吗?
已知:如图,在△ABC 中,DE 是 △ABC 的中位线. 求证:
DE∥BC,
DE = BC.
E
A
B
C
D
F
证明:如图,延长 DE 至 F,使 EF = DE,连接 CF.
∵ AE = CE, ∠AED = ∠CEF,
∴△ADE≌△CFE.
∴AD = CF,∠A = ∠ECF.
∴CF∥AB.
∵AD = BD,
∴四边形 DBCF 是平行四边形.
∴BD = CF.
证明猜想
∴DE∥BC,
知识讲解
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
D
A
B
C
E
应用:
∵DE 是 △ABC 的中位线,
∴DE∥BC,
(1) 当在三角形或几何图形中看到中点,尤其是两个或者两个以上的中点时可以联想到三角形的中位线定理.
(2) 三角形的中位线定理既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),所以在解决相关问题时要两方面结合起来灵活应用.
归纳:
已知:如图,在四边形 ABCD 中, E,F,G,H 分别为各边的中点. 求证:四边形 EFGH 是平行四边形.
分析:将四边形 ABCD 分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.
A
B
C
D
E
F
G
H
例
证明:连接 AC.
∵E,F,G,H 分别为各边的中点,
∴ EF∥HG,EF = HG.
∴EF∥AC,
HG∥AC,
∴四边形 EFGH 是平行四边形.
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
不变化
四边形 EFGH 的形状和什么有关?
想一想:若平行四边形 ABCD 变成任意的四边形,其它条件不变,则四边形 EFGH 的形状会变化吗?为什么?
随 堂 小 测
1. 如图,MN 为△ABC 的中位线,若∠ABC = 61°,则∠AMN = °,若 MN = 12 ,则 BC = .
A
M
B
C
N
61
24
A
D
B
C
E
2. 如图,△ABC 中,D ,E 分别为 AB,AC 的中点,当 BC = 10 cm时,则 DE = cm.
5
第1题图
第2题图
3. 已知:三角形的各边分别为 6 cm,8 cm,12 cm,则连接各边中点所成三角形的周长为 ____ cm.
13
4. 已知:三角形的周长为 64 cm,则连接各边中点所成三角形的周长为 ____cm.
32
5. 如图,已知△ABC 中,AB = 3 cm,BC = 3.4 cm,AC = 4 cm 且 D,E,F 分别为 AC,AB,BC 边的中点,则△DEF 的周长是 cm.
A
B
C
D
E
F
5.2
6. 在△ABC 中,中线 CE、BF 相交点 O,M、N 分别是 OB、OC 的中点,则 EF 和 MN 的关系是_______________.
平行且相等
7. A,B 两村相隔一座大山,你能想办法测出 A,B 两村的直线距离 AB 的大小吗?若 MN = 360 m,则 AB = m.
A
B
C
M
N
解析:在 AB 外选一点 C,使 C 能直接到达 A 和 B,连接 AC 和 BC,并分别找出 AC 和 BC 的中点 M、N,测出 MN 的长,就可知 A、B 两点的距离.
720
如果,M、N 两点之间还有阻隔,你有什么解决办法?
两次利用中位线,分别取 CM 和 CN 的中点.
8. 如图,在 Rt△ABC 中,∠C = 90°, D 是斜边 AB 的中点,E 是 BC 的中点.
(2)若 AB = 10,DE = 4, 求△ABC 的面积.
(1)DE⊥BC 吗?为什么?
A
B
C
D
E
∴DE∥BC.
解:∵DE = 4,∴AC = 8.
∵AB = 10,AC = 8,∴BC = 6.
解:∵D、E 分别是 AB、BC 的中点,
∵∠C = 90°,∴∠DEC = 90°. ∴DE⊥BC.
9. 规律探究:(1)△ABC 的周长为 a,
D、E、F分别为△ABC各边中点,△DEF的周长为 ;
G、H、I分别为△DEF各边中点,△GHI的周长为 ;
C
A
B
D
F
E
G
H
I
像这样下去,第 3 个三角形的周长为 ;
第 n 个三角形的周长为 .
你发现了什么?
,…,
(2)已知:△ABC 的面积为 S ,连接各边中点得△A1B1C1,再连接△A1B1C1 各边中点得△A2B2C2 ,…,
则第 1 次连接所得△A1B1C1 面积=____;
第 2 次连接所得△A2B2C2 面积= ;
第 3 次连接所得△A3B3C3 面积= ;
,…,
第 n 次连接所得△AnBnCn 面积= .
A
C
A1
B1
C1
A2
B2
C2
B
C3
A3
B3
次数 1 2 3 … n
所得三角形周长 …
所得三角形面积 …
通过上述题目我们可以得到:
小结
三角形中位线
定 义
连接三角形两边中点的线段叫作三角形的中位线
定 理
三角形的中位线平行于第三边,并且等于第三边的一半
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
