2.5 矩形 第1课时 矩形的性质 课件(共23张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 2.5 矩形 第1课时 矩形的性质 课件(共23张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 566.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第2章 四边形
2.5 矩 形
2.5.1 矩形的性质
学习目标
1.理解矩形的概念,以及矩形与平行四边形的关系.
2.探索并证明矩形的性质定理:矩形的四个角都是直角;矩形对角线相等.
3.会用矩形的性质定理进行推理和计算.
4.理解矩形是中心对称图形,对角线交点是它的对称中心;矩形是轴对称图形,过每组对边的中点的直线都是矩形的对称轴.
学习重点、难点
矩形的性质定理及其应用.
重点:
难点:
探索并证明性质定理“矩形的对角线相等”以及“矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴”.
课时导入
观察
在小学,我们初步认识了长方形,观察下图中的长方形,它是什么平行四边形吗?它有什么特点呢?
你还能举出其他的例子吗?
矩形
活动 1:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请注意观察.
知识讲解
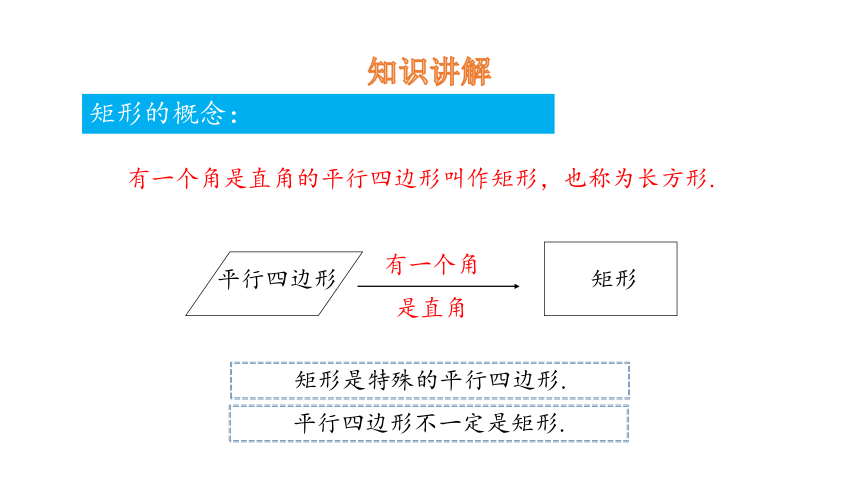
矩形的概念:
有一个角是直角的平行四边形叫作矩形,也称为长方形.
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
活动 2:
准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.
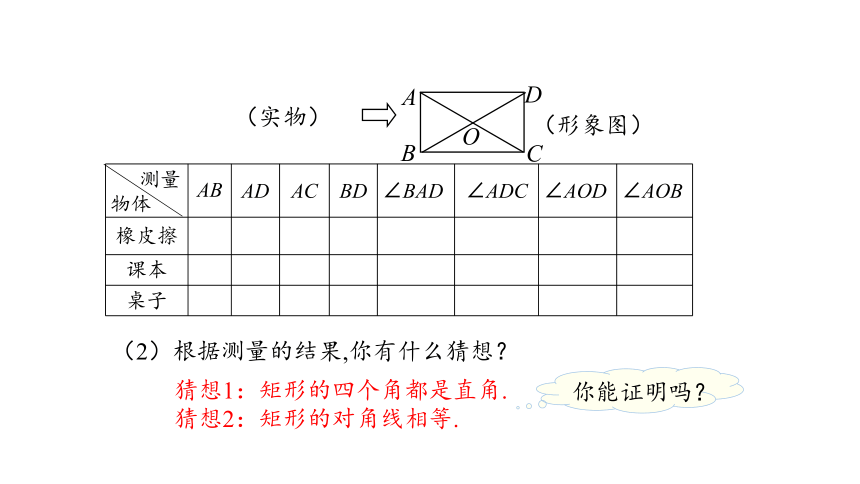
(1) 请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.
A
B
C
D
O
AB AD AC BD ∠BAD ∠ADC ∠AOD ∠AOB
橡皮擦
课本
桌子
物体
测量
(实物)
(形象图)
(2)根据测量的结果,你有什么猜想?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
你能证明吗?
证明猜想
证明:∵四边形 ABCD 是矩形,
∴∠B = ∠D,∠C = ∠A, AB∥DC.
∴∠B +∠C = 180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B = ∠C = ∠D = ∠A = 90°.
如图,四边形 ABCD 是矩形,∠B = 90°.
求证: ∠B = ∠C = ∠D = ∠A = 90°.
A
B
C
D
证明猜想
证明:∵四边形 ABCD 是矩形,
∴AB = DC,∠ABC = ∠DCB = 90°.
在△ABC 和△DCB 中,
∵AB = DC,∠ABC = ∠DCB,BC = CB,
∴△ABC≌△DCB.
∴AC = DB.
A
B
C
D
O
如图,四边形 ABCD 是矩形,∠ABC = 90°,对角线 AC 与 DB 相交于点 O. 求证:AC = DB.
知识讲解
矩形的性质:
矩形的四个角都是直角,对边相等,对角线相等且互相平分.
应用:
在矩形 ABCD 中,对角线 AC 与 DB 相交于点 O,∴∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,AC = DB.
A
B
C
D
O
例
如图,在矩形 ABCD 中,两条对角线 AC,BD 相交于点 O,∠AOB = 60°,AB = 4 ,求矩形对角线的长.
解:∵四边形 ABCD 是矩形.
∴AC = BD,OA = OC = AC,OB = OD = BD.
∴OA = OB.
又∵∠AOB = 60°,
∴△OAB 是等边三角形.
∴OA = AB = 4.
∴AC = BD = 2OA = 8.
A
B
C
D
O
矩形是不是中心对称图形 如果是,那么对称中心是什么?
矩形是中心对称图形,对角线的交点是它的对称中心.
由于矩形是平行四边形,因此:
O
思考
请同学们拿出准备好的矩形纸片,折一折,观察并思考:矩形是不是轴对称图形 如果是,那么对称轴有几条
矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴.
做一做
随 堂 小 测
1. 如图,在矩形 ABCD 中,对角线 AC,BD 交于点 O,
下列说法错误的是 ( )
A.AB∥DC
B.AC = BD
C.AC⊥BD
D.OA = OB
A
B
C
D
O
C
2. 矩形具有而一般平行四边形不具有的性质是 ( )
A. 对角线相等 B. 对边相等
C. 对角相等 D. 对角线互相平分
A
3. 若矩形的一条对角线与一边的夹角为 40°,则两条对角线相交的锐角是 ( )
A. 20° B. 40° C. 80° D. 10°
C
4. 如图,EF 过矩形 ABCD 对角线的交点 O,且分别交 AB、CD 于 E、F,那么阴影部分的面积是矩形ABCD 面积的_________.
5. 如图,在矩形 ABCD 中,对角线 AC、BD 相交于点 O,点 E、F 分别是 AO、AD 的中点,若 AB = 6 cm,BC = 8 cm,则 EF =______cm.
2.5
A
B
C
D
O
E
F
6.如图,在矩形 ABCD 中,E 是 BC 上点,AE = AD,
DF⊥AE ,垂足为 F. 求证:DF = DC.
A
B
C
D
E
F
证明:连接 DE,如图.
∵AD = AE,∴∠AED = ∠ADE.
∵四边形 ABCD 是矩形,
∴AD∥BC,∠C = 90°.
∴∠ADE = ∠DEC.
∴∠DEC = ∠AED.
又∵DF⊥AE,
∴DF = DC.
7. 如图,在矩形 ABCD 中,AE⊥BD 于 E,∠DAE:∠BAE=3∶1,求 ∠BAE 和 ∠EAO 的度数.
解:∵四边形 ABCD 是矩形,
∴∠DAB=90°,AO= AC,BO= BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO.
∴∠OAB=∠ABE,
又∵∠DAE∶∠BAE=3∶1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°
∴∠EAO=67.5°-22.5°=45°.
8. 如图,将矩形 ABCD 沿着直线 BD 折叠,使点C 落在 C′ 处,BC′ 交 AD 于点 E,AD=8,AB=4,求△BED 的面积.
解:∵四边形 ABCD 是矩形,
∴AD∥BC,∠A=90°,∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设 BE=DE=x,则 AE=8-x.
∵在Rt△ABE中,AB2+AE2 = BE2,
∴ 42 + (8-x)2 = x2, 解得 x=5,即 DE=5.
∴S△BED= DE·AB= ×5×4=10.
小结
矩形的相关概念及性质
矩形的四个角都是直角,对边相等
两条对角线互相平分且相等
轴对称图形
有两条对称轴
有一个角是直角的平行四边形叫作矩形
矩形是中心对称图形,对角线的交点是它的对称中心
第2章 四边形
2.5 矩 形
2.5.1 矩形的性质
学习目标
1.理解矩形的概念,以及矩形与平行四边形的关系.
2.探索并证明矩形的性质定理:矩形的四个角都是直角;矩形对角线相等.
3.会用矩形的性质定理进行推理和计算.
4.理解矩形是中心对称图形,对角线交点是它的对称中心;矩形是轴对称图形,过每组对边的中点的直线都是矩形的对称轴.
学习重点、难点
矩形的性质定理及其应用.
重点:
难点:
探索并证明性质定理“矩形的对角线相等”以及“矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴”.
课时导入
观察
在小学,我们初步认识了长方形,观察下图中的长方形,它是什么平行四边形吗?它有什么特点呢?
你还能举出其他的例子吗?
矩形
活动 1:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请注意观察.
知识讲解
矩形的概念:
有一个角是直角的平行四边形叫作矩形,也称为长方形.
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
活动 2:
准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.
(1) 请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.
A
B
C
D
O
AB AD AC BD ∠BAD ∠ADC ∠AOD ∠AOB
橡皮擦
课本
桌子
物体
测量
(实物)
(形象图)
(2)根据测量的结果,你有什么猜想?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
你能证明吗?
证明猜想
证明:∵四边形 ABCD 是矩形,
∴∠B = ∠D,∠C = ∠A, AB∥DC.
∴∠B +∠C = 180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B = ∠C = ∠D = ∠A = 90°.
如图,四边形 ABCD 是矩形,∠B = 90°.
求证: ∠B = ∠C = ∠D = ∠A = 90°.
A
B
C
D
证明猜想
证明:∵四边形 ABCD 是矩形,
∴AB = DC,∠ABC = ∠DCB = 90°.
在△ABC 和△DCB 中,
∵AB = DC,∠ABC = ∠DCB,BC = CB,
∴△ABC≌△DCB.
∴AC = DB.
A
B
C
D
O
如图,四边形 ABCD 是矩形,∠ABC = 90°,对角线 AC 与 DB 相交于点 O. 求证:AC = DB.
知识讲解
矩形的性质:
矩形的四个角都是直角,对边相等,对角线相等且互相平分.
应用:
在矩形 ABCD 中,对角线 AC 与 DB 相交于点 O,∴∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,AC = DB.
A
B
C
D
O
例
如图,在矩形 ABCD 中,两条对角线 AC,BD 相交于点 O,∠AOB = 60°,AB = 4 ,求矩形对角线的长.
解:∵四边形 ABCD 是矩形.
∴AC = BD,OA = OC = AC,OB = OD = BD.
∴OA = OB.
又∵∠AOB = 60°,
∴△OAB 是等边三角形.
∴OA = AB = 4.
∴AC = BD = 2OA = 8.
A
B
C
D
O
矩形是不是中心对称图形 如果是,那么对称中心是什么?
矩形是中心对称图形,对角线的交点是它的对称中心.
由于矩形是平行四边形,因此:
O
思考
请同学们拿出准备好的矩形纸片,折一折,观察并思考:矩形是不是轴对称图形 如果是,那么对称轴有几条
矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴.
做一做
随 堂 小 测
1. 如图,在矩形 ABCD 中,对角线 AC,BD 交于点 O,
下列说法错误的是 ( )
A.AB∥DC
B.AC = BD
C.AC⊥BD
D.OA = OB
A
B
C
D
O
C
2. 矩形具有而一般平行四边形不具有的性质是 ( )
A. 对角线相等 B. 对边相等
C. 对角相等 D. 对角线互相平分
A
3. 若矩形的一条对角线与一边的夹角为 40°,则两条对角线相交的锐角是 ( )
A. 20° B. 40° C. 80° D. 10°
C
4. 如图,EF 过矩形 ABCD 对角线的交点 O,且分别交 AB、CD 于 E、F,那么阴影部分的面积是矩形ABCD 面积的_________.
5. 如图,在矩形 ABCD 中,对角线 AC、BD 相交于点 O,点 E、F 分别是 AO、AD 的中点,若 AB = 6 cm,BC = 8 cm,则 EF =______cm.
2.5
A
B
C
D
O
E
F
6.如图,在矩形 ABCD 中,E 是 BC 上点,AE = AD,
DF⊥AE ,垂足为 F. 求证:DF = DC.
A
B
C
D
E
F
证明:连接 DE,如图.
∵AD = AE,∴∠AED = ∠ADE.
∵四边形 ABCD 是矩形,
∴AD∥BC,∠C = 90°.
∴∠ADE = ∠DEC.
∴∠DEC = ∠AED.
又∵DF⊥AE,
∴DF = DC.
7. 如图,在矩形 ABCD 中,AE⊥BD 于 E,∠DAE:∠BAE=3∶1,求 ∠BAE 和 ∠EAO 的度数.
解:∵四边形 ABCD 是矩形,
∴∠DAB=90°,AO= AC,BO= BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO.
∴∠OAB=∠ABE,
又∵∠DAE∶∠BAE=3∶1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°
∴∠EAO=67.5°-22.5°=45°.
8. 如图,将矩形 ABCD 沿着直线 BD 折叠,使点C 落在 C′ 处,BC′ 交 AD 于点 E,AD=8,AB=4,求△BED 的面积.
解:∵四边形 ABCD 是矩形,
∴AD∥BC,∠A=90°,∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设 BE=DE=x,则 AE=8-x.
∵在Rt△ABE中,AB2+AE2 = BE2,
∴ 42 + (8-x)2 = x2, 解得 x=5,即 DE=5.
∴S△BED= DE·AB= ×5×4=10.
小结
矩形的相关概念及性质
矩形的四个角都是直角,对边相等
两条对角线互相平分且相等
轴对称图形
有两条对称轴
有一个角是直角的平行四边形叫作矩形
矩形是中心对称图形,对角线的交点是它的对称中心
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
