3.1 平面直角坐标系 第1课时 课件(共23张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 3.1 平面直角坐标系 第1课时 课件(共23张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 263.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第3章 图形与坐标
3.1 平面直角坐标系
第1课时 平面直角坐标系
学习目标
1.理解平面直角坐标系的概念. 了解建立了平面直角坐标系后平面上的点与有序实数对一一对应.
2.能画出平面直角坐标系,在给定的直角坐标系中,能根据坐标描出点的位置,由点的位置写出它的坐标.
学习重点、难点
能画出平面直角坐标系,写出平面内点的坐标,并能根据坐标描出点的位置.
重点:
难点:
探索建立平面直角坐标系的过程.
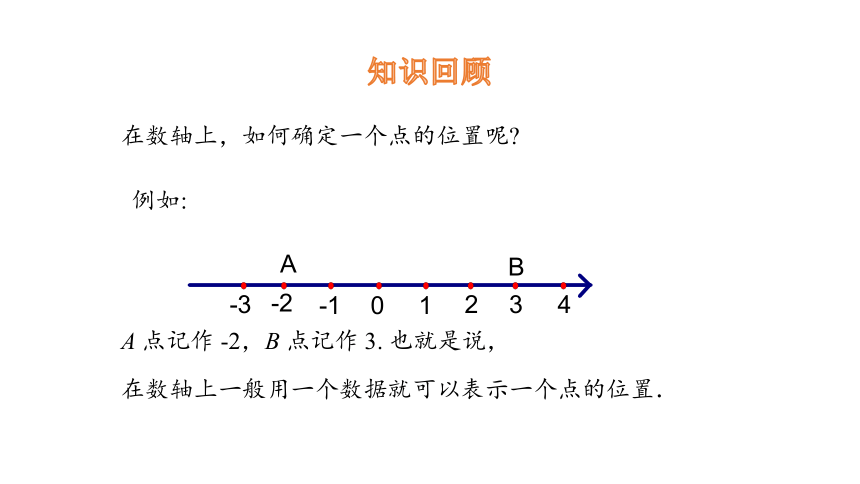
知识回顾
在数轴上,如何确定一个点的位置呢
A 点记作 -2,B 点记作 3. 也就是说,
例如:
在数轴上一般用一个数据就可以表示一个点的位置.
课时导入
思考1 老师在教室里想找一个学生:
提示1:只给一个数据“第 4 组”,你能确定老师要找的学生是谁吗?
提示2:给出两个数据“第 4 组,第 2 排”,你能确定是谁了吗?
生活中,我们常常遇到描述各种物体的位置,说一说,如何确定一位同学在教室里的座位呢?
说一说
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第2排
第4组
(组数,排数)
约定:组数在前,排数在后
(4,2)
(1) 在座位表中“6 组 3 排”与“3 组 6 排”中的“ 6 ”的含义有什么不同?你能找到它们对应的位置吗?
(2) 如果将“6 组 3 排”简记作(6,3),那么“ 3 组 6 排”如何表示?(5,6)表示什么含义? (6,5)呢
(3) 在教室里,确定一个座位一般需要几个数据?
两个数据:组数和排数.
动脑筋
知识讲解
平面直角坐标系的概念:
在平面内画两条互相垂直的数轴,其中一条叫横轴(通常称为 x 轴),另一条叫纵轴(通常称为 y 轴),它们的交点 O 是这两条数轴的原点. 通常,我们取横轴向右为正方向,纵轴向上为正方向,横轴与纵轴的单位长度通常取成一致(有时也可以不一致),这样建立的两条数轴构成平面直角坐标系,记作 Oxy,如右图所示.
y
O
x
1
2
3
4
5
1
2
3
4
5
6
这样 P 点的横坐标是 -2,纵坐标是 3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3).
P(-2,3)就叫做点 P 在平面直角坐标系中的坐标,简称为点 P 的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
如图,点 P 如何表示呢?
再由 P 点向 y 轴画垂线,垂足 N 在 y 轴上的坐标是 3,称为 P 点的纵坐标.
先由 P 点向 x 轴画垂线,垂足 M 在 x 轴上的坐标是 -2,称为 P 点的横坐标.
P
N
M
思考
活动1 观察平面直角坐标系,填写各象限内的点的坐标符号特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
不看平面直角坐标系,你能迅速说出点 A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4) 所在的象限吗?
点的位置 横坐标的符号 纵坐标的
符号
在 x 轴的正半轴上
在 x 轴的负半轴上
在 y 轴的正半轴上
在 y 轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2 观察直角坐标系,填写坐标轴上的点的坐标的特征:
不看平面直角坐标系,你能迅速说出点 (-5,0),(0,-5),(3,0),(0,3),(0,0)所在的位置吗?
思考:坐标平面上的点与有序实数对(坐标)是什么关系
类似数轴上的点与实数一一对应,我们可以得出:
① 对于坐标平面内任意一点 M,都有唯一的一对有序实数 (x,y) (即点 M 的坐标)和它对应;
② 反过来,对于任意一对有序实数(x,y),在坐标平面上都有唯一的一点 M (即坐标为(x,y)的点)和它对应.
也就是说,坐标平面上的点与有序实数对是一一对应的.
A
B
C
E
F
D
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
写出下图中的多边形 ABCDEF 各个顶点的坐标.
例1
例2
设点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a > 0,b < 0 时,点 M 位于第几象限?
(2) 当 ab > 0 时,点 M 位于第几象限?
(3) 当 a 为任意有理数,且 b < 0 时,点 M 位于哪里?
解:(1) 点M 在第四象限.
(2) 可能在第一象限 (a > 0,b > 0) 或者在第三象限( a
< 0,b < 0 ).
(3) 可能在第三象限 (a < 0,b < 0 ) 或者第四象限
(a > 0,b < 0 ) 或者 y 轴负半轴上 (a = 0,b < 0).
随 堂 小 测
1. 如图,点 A 的坐标为 ( )
A. ( -2,3)
B. ( 3,-2)
C . ( -2,-3)
D . ( 2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
2.点 A (m+3,m+1)在 x 轴上,则 A 点的坐标为( )
A. (0,-2) B. (2,0) C. (4,0) D. (0,-4)
【解析】点 A(m+3,m+1)在 x 轴上,根据 x 轴上点的坐标特征知 m+1=0,求出 m 的值代入 m+3 中即可.
B
归纳:坐标轴上的点的坐标特点:x 轴上的点的纵坐标为 0,y 轴上的点的横坐标为 0. 根据点的坐标的特征确定字母取值,进而求出点的坐标.
3.已知点 P 到 x 轴的距离为 2,到 y 轴的距离为 1. 如果过点 P 作两坐标轴的垂线,垂足分别在 x 轴的正半轴上和 y 轴的负半轴上,那么点 P 的坐标是 ( )
A.(2,-1) B.(1,-2) C.(-2,-1) D.(1,2)
解析:由点 P 到 x 轴的距离为 2,到 y 轴的距离为 1,可知点 P 的纵坐标的绝对值为 2,横坐标的绝对值为 1.
又因为过点 P 作两坐标轴的垂线,垂足分别在 x 轴的正半轴上和 y 轴的负半轴上,所以点 P 在第四象限,故其横坐标为正,纵坐标为负. 所以点 P 的坐标是 (1,-2).
B
4. 在 y 轴上的点的横坐标是______,在 x 轴上的点的纵坐标是______.
5. 点 M(-8,12)到 x 轴的距离是______,到 y 轴的距离是______.
0
0
12
8
6. 已知 P 点坐标为(a + 1,a-3).
①若点 P 在 x 轴上,则 a = ;
②若点 P 在 y 轴上,则 a = ;
3
-1
7.在平面直角坐标系中,点 P (m,m-2) 在第一象限内,则 m 的取值范围是_______.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于 m 的一元一次不等式
组 解得 m>2.
m>2
归纳:求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
9. 若点 P(x,y)在第四象限,| x | = 5,| y | = 4,则点 P 的坐标为 .
(5,-4)
8. 已知 a < b < 0,那么点 P(a,-b)在第 象限.
二
10.在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴负半轴上
x 轴负半轴上
原点
11.下列各点分别在坐标平面的什么位置上?
平面直角坐标系
定义:原点、坐标轴
点的坐标
定义与符号特征
描点
点的坐标的确定
小结
第3章 图形与坐标
3.1 平面直角坐标系
第1课时 平面直角坐标系
学习目标
1.理解平面直角坐标系的概念. 了解建立了平面直角坐标系后平面上的点与有序实数对一一对应.
2.能画出平面直角坐标系,在给定的直角坐标系中,能根据坐标描出点的位置,由点的位置写出它的坐标.
学习重点、难点
能画出平面直角坐标系,写出平面内点的坐标,并能根据坐标描出点的位置.
重点:
难点:
探索建立平面直角坐标系的过程.
知识回顾
在数轴上,如何确定一个点的位置呢
A 点记作 -2,B 点记作 3. 也就是说,
例如:
在数轴上一般用一个数据就可以表示一个点的位置.
课时导入
思考1 老师在教室里想找一个学生:
提示1:只给一个数据“第 4 组”,你能确定老师要找的学生是谁吗?
提示2:给出两个数据“第 4 组,第 2 排”,你能确定是谁了吗?
生活中,我们常常遇到描述各种物体的位置,说一说,如何确定一位同学在教室里的座位呢?
说一说
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第2排
第4组
(组数,排数)
约定:组数在前,排数在后
(4,2)
(1) 在座位表中“6 组 3 排”与“3 组 6 排”中的“ 6 ”的含义有什么不同?你能找到它们对应的位置吗?
(2) 如果将“6 组 3 排”简记作(6,3),那么“ 3 组 6 排”如何表示?(5,6)表示什么含义? (6,5)呢
(3) 在教室里,确定一个座位一般需要几个数据?
两个数据:组数和排数.
动脑筋
知识讲解
平面直角坐标系的概念:
在平面内画两条互相垂直的数轴,其中一条叫横轴(通常称为 x 轴),另一条叫纵轴(通常称为 y 轴),它们的交点 O 是这两条数轴的原点. 通常,我们取横轴向右为正方向,纵轴向上为正方向,横轴与纵轴的单位长度通常取成一致(有时也可以不一致),这样建立的两条数轴构成平面直角坐标系,记作 Oxy,如右图所示.
y
O
x
1
2
3
4
5
1
2
3
4
5
6
这样 P 点的横坐标是 -2,纵坐标是 3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3).
P(-2,3)就叫做点 P 在平面直角坐标系中的坐标,简称为点 P 的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
如图,点 P 如何表示呢?
再由 P 点向 y 轴画垂线,垂足 N 在 y 轴上的坐标是 3,称为 P 点的纵坐标.
先由 P 点向 x 轴画垂线,垂足 M 在 x 轴上的坐标是 -2,称为 P 点的横坐标.
P
N
M
思考
活动1 观察平面直角坐标系,填写各象限内的点的坐标符号特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
不看平面直角坐标系,你能迅速说出点 A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4) 所在的象限吗?
点的位置 横坐标的符号 纵坐标的
符号
在 x 轴的正半轴上
在 x 轴的负半轴上
在 y 轴的正半轴上
在 y 轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2 观察直角坐标系,填写坐标轴上的点的坐标的特征:
不看平面直角坐标系,你能迅速说出点 (-5,0),(0,-5),(3,0),(0,3),(0,0)所在的位置吗?
思考:坐标平面上的点与有序实数对(坐标)是什么关系
类似数轴上的点与实数一一对应,我们可以得出:
① 对于坐标平面内任意一点 M,都有唯一的一对有序实数 (x,y) (即点 M 的坐标)和它对应;
② 反过来,对于任意一对有序实数(x,y),在坐标平面上都有唯一的一点 M (即坐标为(x,y)的点)和它对应.
也就是说,坐标平面上的点与有序实数对是一一对应的.
A
B
C
E
F
D
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
写出下图中的多边形 ABCDEF 各个顶点的坐标.
例1
例2
设点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a > 0,b < 0 时,点 M 位于第几象限?
(2) 当 ab > 0 时,点 M 位于第几象限?
(3) 当 a 为任意有理数,且 b < 0 时,点 M 位于哪里?
解:(1) 点M 在第四象限.
(2) 可能在第一象限 (a > 0,b > 0) 或者在第三象限( a
< 0,b < 0 ).
(3) 可能在第三象限 (a < 0,b < 0 ) 或者第四象限
(a > 0,b < 0 ) 或者 y 轴负半轴上 (a = 0,b < 0).
随 堂 小 测
1. 如图,点 A 的坐标为 ( )
A. ( -2,3)
B. ( 3,-2)
C . ( -2,-3)
D . ( 2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
2.点 A (m+3,m+1)在 x 轴上,则 A 点的坐标为( )
A. (0,-2) B. (2,0) C. (4,0) D. (0,-4)
【解析】点 A(m+3,m+1)在 x 轴上,根据 x 轴上点的坐标特征知 m+1=0,求出 m 的值代入 m+3 中即可.
B
归纳:坐标轴上的点的坐标特点:x 轴上的点的纵坐标为 0,y 轴上的点的横坐标为 0. 根据点的坐标的特征确定字母取值,进而求出点的坐标.
3.已知点 P 到 x 轴的距离为 2,到 y 轴的距离为 1. 如果过点 P 作两坐标轴的垂线,垂足分别在 x 轴的正半轴上和 y 轴的负半轴上,那么点 P 的坐标是 ( )
A.(2,-1) B.(1,-2) C.(-2,-1) D.(1,2)
解析:由点 P 到 x 轴的距离为 2,到 y 轴的距离为 1,可知点 P 的纵坐标的绝对值为 2,横坐标的绝对值为 1.
又因为过点 P 作两坐标轴的垂线,垂足分别在 x 轴的正半轴上和 y 轴的负半轴上,所以点 P 在第四象限,故其横坐标为正,纵坐标为负. 所以点 P 的坐标是 (1,-2).
B
4. 在 y 轴上的点的横坐标是______,在 x 轴上的点的纵坐标是______.
5. 点 M(-8,12)到 x 轴的距离是______,到 y 轴的距离是______.
0
0
12
8
6. 已知 P 点坐标为(a + 1,a-3).
①若点 P 在 x 轴上,则 a = ;
②若点 P 在 y 轴上,则 a = ;
3
-1
7.在平面直角坐标系中,点 P (m,m-2) 在第一象限内,则 m 的取值范围是_______.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于 m 的一元一次不等式
组 解得 m>2.
m>2
归纳:求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
9. 若点 P(x,y)在第四象限,| x | = 5,| y | = 4,则点 P 的坐标为 .
(5,-4)
8. 已知 a < b < 0,那么点 P(a,-b)在第 象限.
二
10.在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴负半轴上
x 轴负半轴上
原点
11.下列各点分别在坐标平面的什么位置上?
平面直角坐标系
定义:原点、坐标轴
点的坐标
定义与符号特征
描点
点的坐标的确定
小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
