4.3 一次函数的图象 第2课时 一次函数的图象和性质 课件(共17张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 4.3 一次函数的图象 第2课时 一次函数的图象和性质 课件(共17张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 169.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第4章 一次函数
4.3 一次函数的图象
第2课时 一次函数的图象和性质
课时导入
探究
先画出正比例函数 y = 2x 的图象,然后探索 y = 2x+3 的图象.
x
y = 2x
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
先取自变量 x 的一些值,算出 y = 2x , y = 2x+3 对应的函数值,列成表格如下:
…
…
y = 2x+3
-1
1
3
5
7
y = 2x
描点、连线,作出函数 y = 2x+3 的图象.
y = 2x+3
y = x
y = x + 2
y = x - 2
y
2
O
x
2
●
●
在平面直角坐标系中画出 y = x,y = x+2,y = x-2的图象,观察三个函数图象的平移情况:
3. 比较三个函数的表达式, 相同,它
们的图象的位置关系是 .
比较一次函数 y = x+2,y = x-2 , y = x 的图象,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数 y = x 的图象经过原点,函数 y = x + 2 的图象与
y 轴交于点 ,即它可以看作由直线 y = x 向
平移 个单位长度而得到.函数 y = x - 2 的图
象与 y 轴交于点 ,即它可以看作由直线 y
= x 向____平移____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
自变量系数 k
平行
知识讲解
一次函数的图象:
(0,b)
( ,0)
一次函数 y = kx+b 的图象也称为直线 y = kx+b.
一次函数 y = kx+b 的图象是一条直线,它与正比例函数 y = kx 平行.
一次函数 y = kx + b(k ≠ 0)的图象经过点(0,b),可以由正比例函数 y = kx 的图象平移 个单位长度得到 (当 b>0时,向 平移;当 b<0 时,向 平移).
下
上
| b |
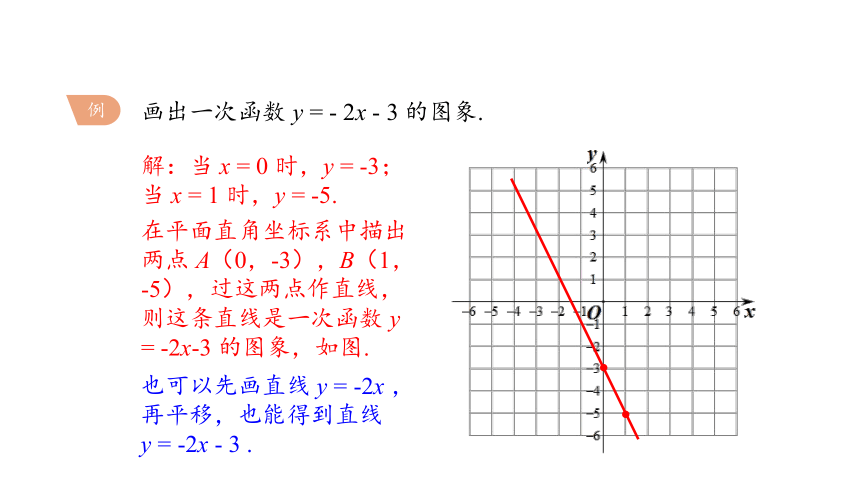
画出一次函数 y = - 2x - 3 的图象.
也可以先画直线 y = -2x ,再平移,也能得到直线
y = -2x - 3 .
例
解:当 x = 0 时,y = -3;
当 x = 1 时,y = -5.
在平面直角坐标系中描出两点 A(0,-3),B(1,-5),过这两点作直线,则这条直线是一次函数 y = -2x-3 的图象,如图.
议一议
观察画出的一次函数y = 2x + 3,y = 2x - 3的图象.
y = 2x - 3
y = 2x + 3
你能发现当自变量 x 的取值由小变大时,对应的函数值如何变化吗
在一次函数 y = kx + b (k, b 为常数, k ≠ 0) 中,
当 k>0 时,y 的值随着 x 值的增大而增大;
当 k<0 时,y 的值随着 x 值的增大而减小.
知识讲解
一次函数的性质:
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
根据一次函数的图象判断 k,b 的正负,并说出直线经过的象限:
>
>
>
>
<
=
>
<
<
<
<
=
思考
由上可知,在一次函数 y = kx+b 中,
当 k>0 时,直线 y = kx+b 从左到右逐渐上升,y 随 x 的增大而增大.
当 k<0 时,直线 y = kx+b 从左到右逐渐下降,y 随 x 的增大而减小.
① b>0 时,直线经过第一、二、四象限;
② b<0 时,直线经过第二、三、四象限.
① b>0 时,直线经过第一、二、三象限;
② b<0 时,直线经过第一、三、四象限.
随 堂 小 测
1.将直线 y = 2x 向上平移 2 个单位后所得图象对应的函数表达式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
D
2.两个一次函数 y1 = ax+b 与 y2 = bx+a,它们在同一坐标系中的图象可能是( )
C
3.下列函数中,y 的值随 x 值的增大而增大的函数是 ( )
A. y = -2x B. y = -2x + 1
C. y = x - 2 D. y = -x - 2
C
4.P1(x1,y1),P2(x2,y2) 是一次函数 y = -0.5x + 3 图象
上的两点,下列判断中,正确的是 ( )
A. y1>y2 B. 当 x1<x2 时,y1<y2
C. y1<y2 D. 当 x1<x2 时,y1>y2
D
5.将正比例函数 y=-6x 的图象向上平移,则平移后所得图象对应的函数表达式可能是 _____________
(写出一个即可).
y=-6x+3
6. 直线 y = x + 2 可由直线 y = x - 1向 平移 个单位得到.
上
3
7. 点 A(-1,y1),B(3,y2) 是直线 y = kx + b(k < 0)上的两点,则 y1 - y2 0 (填“>”或“<”).
>
8.已知一次函数 y = (1 - 2m)x + m - 1,求满足下列条件的 m 的值:
(1)函数值 y 随 x 的增大而增大;
(2)函数图象与 y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限.
解:(1) 由题意得 1 - 2m>0,解得
(2) 由题意得 1 - 2m≠0 且 m - 1 < 0,即
(3) 由题意得 1 - 2m < 0 且 m - 1 < 0,解得
小结
一次函数的图象和性质
当 k > 0 时,y 的值随 x 值的增大而增大;
当 k < 0 时,y 的值随 x 值的增大而减小
与 y 轴的交点是(0,b),
与 x 轴的交点是( ,0);
当 k > 0, b > 0 时,经过一、二、三象限;
当 k > 0 ,b < 0 时,经过一、三、四象限;
当 k < 0 ,b > 0 时,经过一、二、四象限;
当 k < 0 ,b < 0 时,经过二、三、四象限
图象
性质
第4章 一次函数
4.3 一次函数的图象
第2课时 一次函数的图象和性质
课时导入
探究
先画出正比例函数 y = 2x 的图象,然后探索 y = 2x+3 的图象.
x
y = 2x
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
先取自变量 x 的一些值,算出 y = 2x , y = 2x+3 对应的函数值,列成表格如下:
…
…
y = 2x+3
-1
1
3
5
7
y = 2x
描点、连线,作出函数 y = 2x+3 的图象.
y = 2x+3
y = x
y = x + 2
y = x - 2
y
2
O
x
2
●
●
在平面直角坐标系中画出 y = x,y = x+2,y = x-2的图象,观察三个函数图象的平移情况:
3. 比较三个函数的表达式, 相同,它
们的图象的位置关系是 .
比较一次函数 y = x+2,y = x-2 , y = x 的图象,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数 y = x 的图象经过原点,函数 y = x + 2 的图象与
y 轴交于点 ,即它可以看作由直线 y = x 向
平移 个单位长度而得到.函数 y = x - 2 的图
象与 y 轴交于点 ,即它可以看作由直线 y
= x 向____平移____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
自变量系数 k
平行
知识讲解
一次函数的图象:
(0,b)
( ,0)
一次函数 y = kx+b 的图象也称为直线 y = kx+b.
一次函数 y = kx+b 的图象是一条直线,它与正比例函数 y = kx 平行.
一次函数 y = kx + b(k ≠ 0)的图象经过点(0,b),可以由正比例函数 y = kx 的图象平移 个单位长度得到 (当 b>0时,向 平移;当 b<0 时,向 平移).
下
上
| b |
画出一次函数 y = - 2x - 3 的图象.
也可以先画直线 y = -2x ,再平移,也能得到直线
y = -2x - 3 .
例
解:当 x = 0 时,y = -3;
当 x = 1 时,y = -5.
在平面直角坐标系中描出两点 A(0,-3),B(1,-5),过这两点作直线,则这条直线是一次函数 y = -2x-3 的图象,如图.
议一议
观察画出的一次函数y = 2x + 3,y = 2x - 3的图象.
y = 2x - 3
y = 2x + 3
你能发现当自变量 x 的取值由小变大时,对应的函数值如何变化吗
在一次函数 y = kx + b (k, b 为常数, k ≠ 0) 中,
当 k>0 时,y 的值随着 x 值的增大而增大;
当 k<0 时,y 的值随着 x 值的增大而减小.
知识讲解
一次函数的性质:
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
根据一次函数的图象判断 k,b 的正负,并说出直线经过的象限:
>
>
>
>
<
=
>
<
<
<
<
=
思考
由上可知,在一次函数 y = kx+b 中,
当 k>0 时,直线 y = kx+b 从左到右逐渐上升,y 随 x 的增大而增大.
当 k<0 时,直线 y = kx+b 从左到右逐渐下降,y 随 x 的增大而减小.
① b>0 时,直线经过第一、二、四象限;
② b<0 时,直线经过第二、三、四象限.
① b>0 时,直线经过第一、二、三象限;
② b<0 时,直线经过第一、三、四象限.
随 堂 小 测
1.将直线 y = 2x 向上平移 2 个单位后所得图象对应的函数表达式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
D
2.两个一次函数 y1 = ax+b 与 y2 = bx+a,它们在同一坐标系中的图象可能是( )
C
3.下列函数中,y 的值随 x 值的增大而增大的函数是 ( )
A. y = -2x B. y = -2x + 1
C. y = x - 2 D. y = -x - 2
C
4.P1(x1,y1),P2(x2,y2) 是一次函数 y = -0.5x + 3 图象
上的两点,下列判断中,正确的是 ( )
A. y1>y2 B. 当 x1<x2 时,y1<y2
C. y1<y2 D. 当 x1<x2 时,y1>y2
D
5.将正比例函数 y=-6x 的图象向上平移,则平移后所得图象对应的函数表达式可能是 _____________
(写出一个即可).
y=-6x+3
6. 直线 y = x + 2 可由直线 y = x - 1向 平移 个单位得到.
上
3
7. 点 A(-1,y1),B(3,y2) 是直线 y = kx + b(k < 0)上的两点,则 y1 - y2 0 (填“>”或“<”).
>
8.已知一次函数 y = (1 - 2m)x + m - 1,求满足下列条件的 m 的值:
(1)函数值 y 随 x 的增大而增大;
(2)函数图象与 y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限.
解:(1) 由题意得 1 - 2m>0,解得
(2) 由题意得 1 - 2m≠0 且 m - 1 < 0,即
(3) 由题意得 1 - 2m < 0 且 m - 1 < 0,解得
小结
一次函数的图象和性质
当 k > 0 时,y 的值随 x 值的增大而增大;
当 k < 0 时,y 的值随 x 值的增大而减小
与 y 轴的交点是(0,b),
与 x 轴的交点是( ,0);
当 k > 0, b > 0 时,经过一、二、三象限;
当 k > 0 ,b < 0 时,经过一、三、四象限;
当 k < 0 ,b > 0 时,经过一、二、四象限;
当 k < 0 ,b < 0 时,经过二、三、四象限
图象
性质
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
