4.4 用待定系数法确定一次函数表达式 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 4.4 用待定系数法确定一次函数表达式 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 218.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第4章 一次函数
4.4 用待定系数法确定一次函数表达式
学习目标
1.会利用待定系数法确定一次函数的表达式.
2.能利用建立一次函数模型解决简单实际问题.
学习重点、难点
用待定系数法确定一次函数的表达式.
重点:
难点:
利用一次函数表达式解决简单实际问题.
课时导入
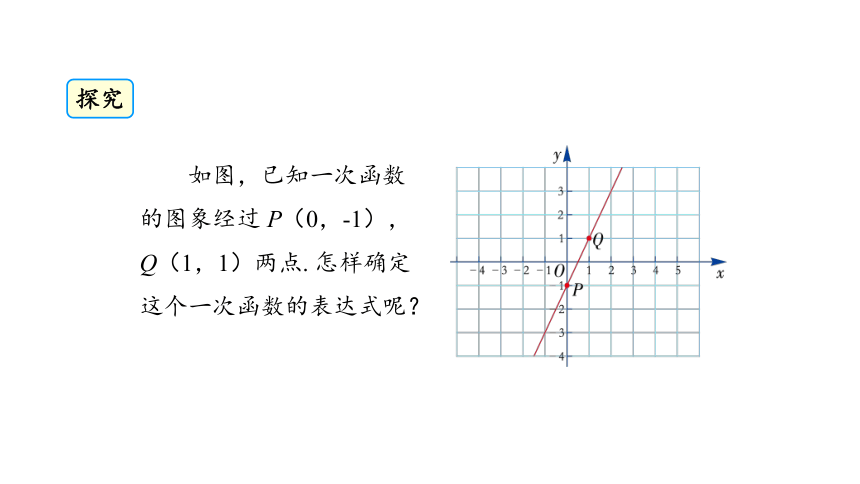
许多实际问题的解决都需要求出一次函数的表达式,在前面,我们已经知道了:一次函数的图象是一条直线,通过两点确定一条直线,我们取函数上的两个自变量值及其相应的函数值即可画出该一次函数的图象.
思考:反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的表达式吗?
探究
如图,已知一次函数的图象经过 P(0,-1),
Q(1,1)两点. 怎样确定这个一次函数的表达式呢?
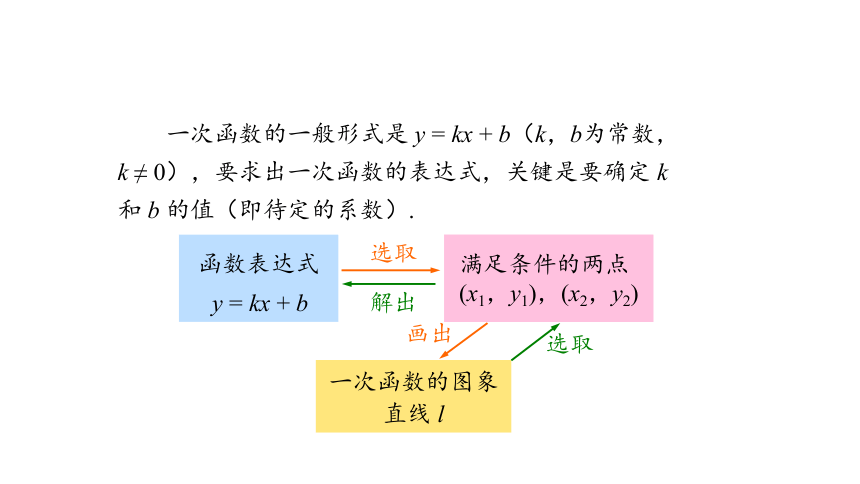
一次函数的一般形式是 y = kx + b(k,b为常数,k ≠ 0),要求出一次函数的表达式,关键是要确定 k 和 b 的值(即待定的系数).
函数表达式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象
直线 l
选取
解出
画出
选取
∵ 点 P (0,-1) 和 Q (1,1) 都在该函数图象上,
∴ 它们的坐标应满足 y = kx + b,将这两点的坐标代入该式中,得到一个关于 k,b 的二元一次方程组:
∴ 该一次函数的表达式为 y = 2x - 1.
k·0 + b = -1,
k + b = 1.
解这个方程组,得
k = 2,
b = -1.
知识讲解
待定系数法的概念:
像这样,通过先设出函数表达式(确定函数模型),再根据条件确定表达式中的未知系数,从而求出函数表达式的方法称为待定系数法.
议一议
确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
一个
两个
例1
温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数 y 与摄氏度数 x 之间是一次函数关系,如表列出了部分华氏度与摄氏度之间的对应关系:
根据表格中给出的数据,求 y 关于 x 的函数表达式.
某种拖拉机的油箱可储油 40 L,加满油并开始工作后,油箱中的剩余油量 y(L)与工作时间 x(h)(0≤x≤8)之间为一次函数关系,函数图象如图所示.
(1)求 y 关于 x 的函数表达式;
(2)一箱油可供拖拉机工作几
小时?
y = -5x + 40.
8 h
例2
知识讲解
利用二元一次方程组求一次函数表达式的一般步骤:
1. 设出含字母系数的一次函数表达式:y = kx + b;
2. 将已知条件代入上述表达式中,得到关于 k,b 的二元一次方程组;
3. 解这个二元一次方程组,得 k,b 的值;
4. 写出一次函数的表达式.
随 堂 小 测
1. 一次函数 y = kx + b (k ≠ 0) 的图象如图,则下列结论正确的是 ( )
A.k = 2 B.k = 3 C.b = 2 D.b = 3
D
y
x
O
2
3
2. 已知一次函数 y = kx + 5 的图象经过点(-1,2),则
k =_____.
3. 已知函数 y = 2x + b 的图象经过点 (a,7) 和 (-2,a),
则这个函数的表达式为____________.
3
y = 2x + 5
4. 如图,直线 l 是一次函数 y = kx + b 的图象,填空:
(1) b = ______,k =______;
(2) 当 x = 30 时,y =______;
(3) 当 y = 30 时,x =______.
2
-18
-42
l
x
y
解:设直线 l 为 y = kx + b,
∵ l 与直线 y = -2x 平行,∴ k = -2.
又∵ 直线过点 (0,2),
∴ 2 = -2×0 + b.
∴ b = 2.
∴直线 l 的表达式为 y = -2x + 2.
5. 已知直线 l 与直线 y = -2x 平行,且与 y 轴交于点 (0,2),求直线 l 的表达式.
6. 在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数. 一根弹簧不挂物体时长 14.5 厘米;当所挂物体的质量为 3 千克时,弹簧长 16 厘米. 请写出 y 与 x 之间的关系式,并求当所挂物体的质量为 4 千克时弹簧的长度.
解:设 y = kx + b (k ≠ 0)
由题意,得 14.5 = b,16 = 3k + b,解得 b=14.5,k=0.5.
∴在弹性限度内,y = 0.5x + 14.5.
当 x = 4 时,y = 0.5×4+14.5 = 16.5(厘米).
故当所挂物体的质量为 4 千克时弹簧的长度为 16.5 厘米.
解:∵ y 是 x 的一次函数,设其表达式为 y = kx + b,
由题意得 解得
4k + b = 5,
5k + b = 2,
7.已知一个一次函数,当自变量 x = 4时,函数值 y = 5;当 x = 5 时,y = 2. 你能画出它的图象,并写出函数表达式吗?
∴函数表达式为 y = -3x + 17,其图象如图所示.
k = -3,
b = 17.
y
x
o
8. 已知一次函数的图象过点 (0,2),且与两坐标轴围成的三角形的面积为 2,求此一次函数的表达式.
解:设一次函数的表达式为 y = kx + b (k ≠ 0).
∵ 一次函数 y = kx + b 的图象过点 (0,2),
∴ b = 2.
∵ 一次函数的图象与 x 轴的交点是( ,0),
则 解得 k = 1 或 -1.
故此一次函数的表达式为 y = x + 2 或 y = -x + 2.
小结
用待定系数法确定一次函数表达式
2. 根据已知条件列出关于 k,b 的方程组;
1. 设所求的一次函数表达式为 y = kx + b;
3. 解方程组,求出 k,b 值;
4. 把求出的 k,b 代回表达式即可.
第4章 一次函数
4.4 用待定系数法确定一次函数表达式
学习目标
1.会利用待定系数法确定一次函数的表达式.
2.能利用建立一次函数模型解决简单实际问题.
学习重点、难点
用待定系数法确定一次函数的表达式.
重点:
难点:
利用一次函数表达式解决简单实际问题.
课时导入
许多实际问题的解决都需要求出一次函数的表达式,在前面,我们已经知道了:一次函数的图象是一条直线,通过两点确定一条直线,我们取函数上的两个自变量值及其相应的函数值即可画出该一次函数的图象.
思考:反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的表达式吗?
探究
如图,已知一次函数的图象经过 P(0,-1),
Q(1,1)两点. 怎样确定这个一次函数的表达式呢?
一次函数的一般形式是 y = kx + b(k,b为常数,k ≠ 0),要求出一次函数的表达式,关键是要确定 k 和 b 的值(即待定的系数).
函数表达式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象
直线 l
选取
解出
画出
选取
∵ 点 P (0,-1) 和 Q (1,1) 都在该函数图象上,
∴ 它们的坐标应满足 y = kx + b,将这两点的坐标代入该式中,得到一个关于 k,b 的二元一次方程组:
∴ 该一次函数的表达式为 y = 2x - 1.
k·0 + b = -1,
k + b = 1.
解这个方程组,得
k = 2,
b = -1.
知识讲解
待定系数法的概念:
像这样,通过先设出函数表达式(确定函数模型),再根据条件确定表达式中的未知系数,从而求出函数表达式的方法称为待定系数法.
议一议
确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
一个
两个
例1
温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数 y 与摄氏度数 x 之间是一次函数关系,如表列出了部分华氏度与摄氏度之间的对应关系:
根据表格中给出的数据,求 y 关于 x 的函数表达式.
某种拖拉机的油箱可储油 40 L,加满油并开始工作后,油箱中的剩余油量 y(L)与工作时间 x(h)(0≤x≤8)之间为一次函数关系,函数图象如图所示.
(1)求 y 关于 x 的函数表达式;
(2)一箱油可供拖拉机工作几
小时?
y = -5x + 40.
8 h
例2
知识讲解
利用二元一次方程组求一次函数表达式的一般步骤:
1. 设出含字母系数的一次函数表达式:y = kx + b;
2. 将已知条件代入上述表达式中,得到关于 k,b 的二元一次方程组;
3. 解这个二元一次方程组,得 k,b 的值;
4. 写出一次函数的表达式.
随 堂 小 测
1. 一次函数 y = kx + b (k ≠ 0) 的图象如图,则下列结论正确的是 ( )
A.k = 2 B.k = 3 C.b = 2 D.b = 3
D
y
x
O
2
3
2. 已知一次函数 y = kx + 5 的图象经过点(-1,2),则
k =_____.
3. 已知函数 y = 2x + b 的图象经过点 (a,7) 和 (-2,a),
则这个函数的表达式为____________.
3
y = 2x + 5
4. 如图,直线 l 是一次函数 y = kx + b 的图象,填空:
(1) b = ______,k =______;
(2) 当 x = 30 时,y =______;
(3) 当 y = 30 时,x =______.
2
-18
-42
l
x
y
解:设直线 l 为 y = kx + b,
∵ l 与直线 y = -2x 平行,∴ k = -2.
又∵ 直线过点 (0,2),
∴ 2 = -2×0 + b.
∴ b = 2.
∴直线 l 的表达式为 y = -2x + 2.
5. 已知直线 l 与直线 y = -2x 平行,且与 y 轴交于点 (0,2),求直线 l 的表达式.
6. 在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数. 一根弹簧不挂物体时长 14.5 厘米;当所挂物体的质量为 3 千克时,弹簧长 16 厘米. 请写出 y 与 x 之间的关系式,并求当所挂物体的质量为 4 千克时弹簧的长度.
解:设 y = kx + b (k ≠ 0)
由题意,得 14.5 = b,16 = 3k + b,解得 b=14.5,k=0.5.
∴在弹性限度内,y = 0.5x + 14.5.
当 x = 4 时,y = 0.5×4+14.5 = 16.5(厘米).
故当所挂物体的质量为 4 千克时弹簧的长度为 16.5 厘米.
解:∵ y 是 x 的一次函数,设其表达式为 y = kx + b,
由题意得 解得
4k + b = 5,
5k + b = 2,
7.已知一个一次函数,当自变量 x = 4时,函数值 y = 5;当 x = 5 时,y = 2. 你能画出它的图象,并写出函数表达式吗?
∴函数表达式为 y = -3x + 17,其图象如图所示.
k = -3,
b = 17.
y
x
o
8. 已知一次函数的图象过点 (0,2),且与两坐标轴围成的三角形的面积为 2,求此一次函数的表达式.
解:设一次函数的表达式为 y = kx + b (k ≠ 0).
∵ 一次函数 y = kx + b 的图象过点 (0,2),
∴ b = 2.
∵ 一次函数的图象与 x 轴的交点是( ,0),
则 解得 k = 1 或 -1.
故此一次函数的表达式为 y = x + 2 或 y = -x + 2.
小结
用待定系数法确定一次函数表达式
2. 根据已知条件列出关于 k,b 的方程组;
1. 设所求的一次函数表达式为 y = kx + b;
3. 解方程组,求出 k,b 值;
4. 把求出的 k,b 代回表达式即可.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
