4.5 一次函数的应用 第2课时 课件(共17张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 4.5 一次函数的应用 第2课时 课件(共17张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第4章 一次函数
4.5 一次函数的应用
第2课时 建立一次函数模型解决数据预测类型的问题
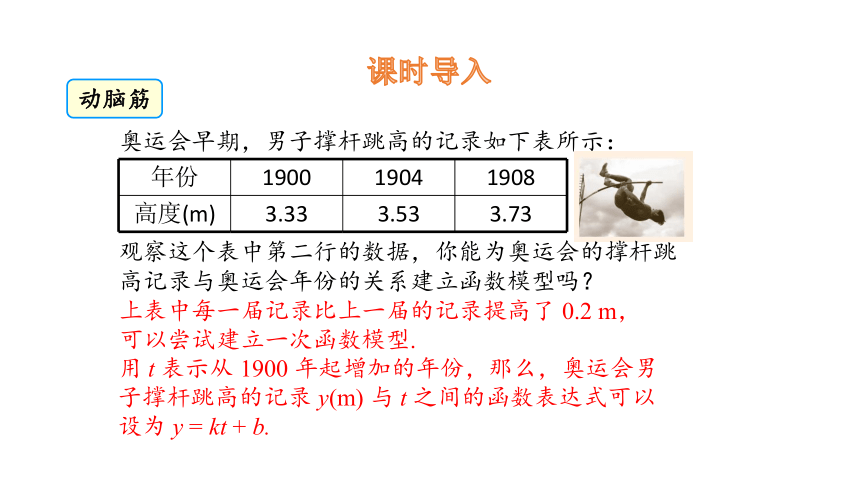
课时导入
动脑筋
奥运会早期,男子撑杆跳高的记录如下表所示:
年份 1900 1904 1908
高度(m) 3.33 3.53 3.73
观察这个表中第二行的数据,你能为奥运会的撑杆跳高记录与奥运会年份的关系建立函数模型吗?
上表中每一届记录比上一届的记录提高了 0.2 m,可以尝试建立一次函数模型.
用 t 表示从 1900 年起增加的年份,那么,奥运会男子撑杆跳高的记录 y(m) 与 t 之间的函数表达式可以设为 y = kt + b.
由于 t = 0 (即1900年) 时,撑杆跳高的记录为 3.33 m;
t = 4 (即1904年) 时,记录为 3.53 m,因此
b = 3.33,
4k + b = 3.53.
解得 k = 0.05, b = 3.33.
于是 y = 0.05t + 3.33. ①
当 t = 8 时,y = 3.73,这说明 1908 年的撑杆跳高记录也符合公式①.
公式①就是奥运会早期男子撑杆跳高记录 y 与 t 之间的函数表达式.
能利用公式 ① 预测 1912 年奥运会男子撑杆跳高记录吗 ?
y = 0.05×12 + 3.33 = 3.93.
实际上,1912 年奥运会男子跳高记录约为 3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.
能利用公式 ① 预测 20 世纪 80 年代,譬如 1988 年奥运会男子撑杆跳高的记录吗?
y = 0.05×88 + 3.33 = 7.73.
然而,1988 年奥运会的男子撑杆跳高记录是 5.90 m,远低于 7.73 m. 这表明用所建立的函数模型远离已知数据做预测是不可靠的.
例
请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:
指距 x(cm) 19 20 21
身高 y(cm) 151 160 169
(1) 求身高 y 与指距 x 之间的函数表达式;
(2) 当李华的指距为 22 cm 时,你能预测他的身高吗?
解:设身高 y 与指距 x 之间的函数表达式为 y = kx + b.
将 x = 19, y = 151 与 x = 20,y = 160 代入上式,得
19k + b = 151,
20k + b = 160.
(1) 求身高 y 与指距 x 之间的函数表达式;
解得 k = 9,b = -20.
于是 y = 9x - 20. ①
将 x = 21,y = 169 代入①式也符合.
公式①就是身高 y 与指距 x 之间的函数表达式.
解:当 x = 22 时, y = 9×22 - 20 = 178.
因此,李华的身高大约是 178 cm.
(2)当李华的指距为 22 cm 时,你能测算他的身高吗?
随 堂 小 测
1.小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x (厘米) … 22 23 24 25 26 …
y (码) … 34 36 38 40 42 …
(1)根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
解:这些点在一条直线上,如图所示.
30
32
38
36
34
40
23
25
24
21
22
27
26
y (码)
x(厘米)
O
(2)据说某篮球巨人的鞋子长 31 cm,那么你知道他穿多大码的鞋子吗?
解:我们选取点(22,34)及点(25,40)的坐标代入y = kx + b中,得
22k + b = 34,
25k + b = 40.
解得 k = 2,b = -10.
∴ 一次函数的表达式为 y = 2x - 10.
把 x = 31 代入上式,得 y = 2×31 - 10 = 52.
∴可以得到某篮球巨人穿 52 码的鞋子.
2. 世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(℉)计量法. 两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/℉ 32 50 68 86 104 122
(1) 在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想 y 与 x 之间的函数关系;
(2) 确定 y 与 x 之间的函数表达式,并检验;
(3) 华氏 0 度时的温度应是多少摄氏度?
(4) 华氏温度的值与对应的摄氏温度的值有相等的可能吗?
(1) 在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想 y 与 x 之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y 与 x 之间的函数关系为一次函数.
(2) 确定 y 与 x 之间的函数表达式,并检验;
解:设 y = kx+b,把 (0,32) 和 (10,50) 代入得
解得
经检验,点 (20,68),(30,86),
(40,104),(50,122) 的坐标均
能满足上述表达式,
∴y 与 x 之间的函数表达式为
(3)华氏 0 度时的温度应是多少摄氏度?
解:当 y = 0 时,
解得
∴华氏 0 度时的温度应是 ℃.
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
解:把 y = x 代入,
解得
∴ 华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
3.下图是用棋子摆成的“上”字 ,则第 n 个图共有多少枚棋子?
图1
图2
图3
图4
解:先列表:
x 1 2 3 …
y 6 10 14 …
描点:如图所示.
我们发现图形的形状为一条直线,故可设该直线为 y = kx + b.
选取点(1,6)及
点(2,10)的坐标代入
y = kx + b 中,
得
k+b=6,
2k+b=10.
解得 k = 4,b = 2.
∴一次函数的表达式为 y = 4x + 2.
令 x = n,则 y = 4n + 2.
∴ 第 n 个图形有 (4n+2) 棋子.
小结
一次函数模型的应用
①将实验得到的数据在平面直角坐标系中描出
②观察这些点的特征,确定选用的函数模型,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
第4章 一次函数
4.5 一次函数的应用
第2课时 建立一次函数模型解决数据预测类型的问题
课时导入
动脑筋
奥运会早期,男子撑杆跳高的记录如下表所示:
年份 1900 1904 1908
高度(m) 3.33 3.53 3.73
观察这个表中第二行的数据,你能为奥运会的撑杆跳高记录与奥运会年份的关系建立函数模型吗?
上表中每一届记录比上一届的记录提高了 0.2 m,可以尝试建立一次函数模型.
用 t 表示从 1900 年起增加的年份,那么,奥运会男子撑杆跳高的记录 y(m) 与 t 之间的函数表达式可以设为 y = kt + b.
由于 t = 0 (即1900年) 时,撑杆跳高的记录为 3.33 m;
t = 4 (即1904年) 时,记录为 3.53 m,因此
b = 3.33,
4k + b = 3.53.
解得 k = 0.05, b = 3.33.
于是 y = 0.05t + 3.33. ①
当 t = 8 时,y = 3.73,这说明 1908 年的撑杆跳高记录也符合公式①.
公式①就是奥运会早期男子撑杆跳高记录 y 与 t 之间的函数表达式.
能利用公式 ① 预测 1912 年奥运会男子撑杆跳高记录吗 ?
y = 0.05×12 + 3.33 = 3.93.
实际上,1912 年奥运会男子跳高记录约为 3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.
能利用公式 ① 预测 20 世纪 80 年代,譬如 1988 年奥运会男子撑杆跳高的记录吗?
y = 0.05×88 + 3.33 = 7.73.
然而,1988 年奥运会的男子撑杆跳高记录是 5.90 m,远低于 7.73 m. 这表明用所建立的函数模型远离已知数据做预测是不可靠的.
例
请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:
指距 x(cm) 19 20 21
身高 y(cm) 151 160 169
(1) 求身高 y 与指距 x 之间的函数表达式;
(2) 当李华的指距为 22 cm 时,你能预测他的身高吗?
解:设身高 y 与指距 x 之间的函数表达式为 y = kx + b.
将 x = 19, y = 151 与 x = 20,y = 160 代入上式,得
19k + b = 151,
20k + b = 160.
(1) 求身高 y 与指距 x 之间的函数表达式;
解得 k = 9,b = -20.
于是 y = 9x - 20. ①
将 x = 21,y = 169 代入①式也符合.
公式①就是身高 y 与指距 x 之间的函数表达式.
解:当 x = 22 时, y = 9×22 - 20 = 178.
因此,李华的身高大约是 178 cm.
(2)当李华的指距为 22 cm 时,你能测算他的身高吗?
随 堂 小 测
1.小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x (厘米) … 22 23 24 25 26 …
y (码) … 34 36 38 40 42 …
(1)根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
解:这些点在一条直线上,如图所示.
30
32
38
36
34
40
23
25
24
21
22
27
26
y (码)
x(厘米)
O
(2)据说某篮球巨人的鞋子长 31 cm,那么你知道他穿多大码的鞋子吗?
解:我们选取点(22,34)及点(25,40)的坐标代入y = kx + b中,得
22k + b = 34,
25k + b = 40.
解得 k = 2,b = -10.
∴ 一次函数的表达式为 y = 2x - 10.
把 x = 31 代入上式,得 y = 2×31 - 10 = 52.
∴可以得到某篮球巨人穿 52 码的鞋子.
2. 世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(℉)计量法. 两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/℉ 32 50 68 86 104 122
(1) 在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想 y 与 x 之间的函数关系;
(2) 确定 y 与 x 之间的函数表达式,并检验;
(3) 华氏 0 度时的温度应是多少摄氏度?
(4) 华氏温度的值与对应的摄氏温度的值有相等的可能吗?
(1) 在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想 y 与 x 之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y 与 x 之间的函数关系为一次函数.
(2) 确定 y 与 x 之间的函数表达式,并检验;
解:设 y = kx+b,把 (0,32) 和 (10,50) 代入得
解得
经检验,点 (20,68),(30,86),
(40,104),(50,122) 的坐标均
能满足上述表达式,
∴y 与 x 之间的函数表达式为
(3)华氏 0 度时的温度应是多少摄氏度?
解:当 y = 0 时,
解得
∴华氏 0 度时的温度应是 ℃.
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
解:把 y = x 代入,
解得
∴ 华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
3.下图是用棋子摆成的“上”字 ,则第 n 个图共有多少枚棋子?
图1
图2
图3
图4
解:先列表:
x 1 2 3 …
y 6 10 14 …
描点:如图所示.
我们发现图形的形状为一条直线,故可设该直线为 y = kx + b.
选取点(1,6)及
点(2,10)的坐标代入
y = kx + b 中,
得
k+b=6,
2k+b=10.
解得 k = 4,b = 2.
∴一次函数的表达式为 y = 4x + 2.
令 x = n,则 y = 4n + 2.
∴ 第 n 个图形有 (4n+2) 棋子.
小结
一次函数模型的应用
①将实验得到的数据在平面直角坐标系中描出
②观察这些点的特征,确定选用的函数模型,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
