5.1 频数与频率 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册
文档属性
| 名称 | 5.1 频数与频率 课件(共20张PPT) 2023-2024学年数学湘教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 157.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 11:37:39 | ||
图片预览





文档简介
(共20张PPT)
第5章 数据的频数分布
5.1 频数与频率
学习目标
1.通过实例和统计活动,感受频数和频率在各种实际问题中的具体涵义和共同本质,以形成关于频数(率)的一般概念,理解这些概念的意义和作用.
2.理解频数与频率之间的相互关系,会统计频数、计算频率.
3.认识频数分布是反映数据的分布,是对于数据的全面刻画.
4.了解频数、频率的一些简单实际应用,通过收集、分析数据的过程,初步作出合理的决策,提高处理问题、决策问题的能力.
学习重点、难点
对于频数、频率意义的理解.
重点:
难点:
对于重复试验理解其试验结果发生的频数、频率的意义.
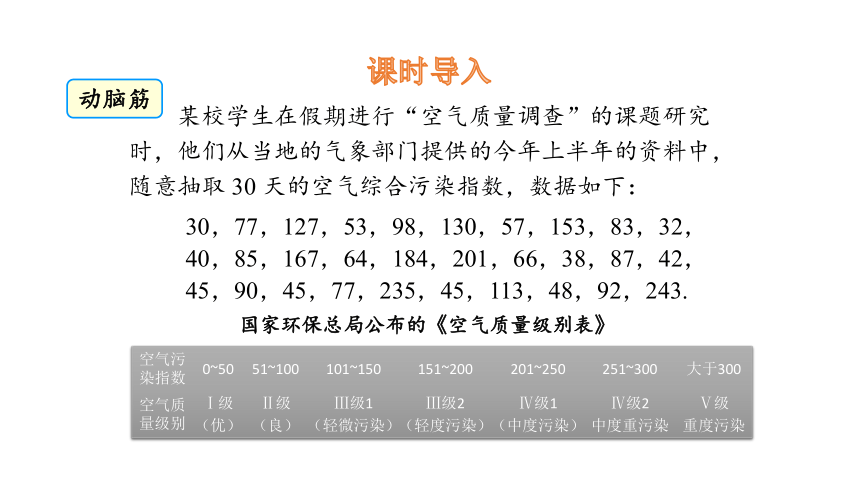
课时导入
动脑筋
某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取 30 天的空气综合污染指数,数据如下:
国家环保总局公布的《空气质量级别表》
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 中度重污染 Ⅴ级
重度污染
(1)说说这 30 天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况);
(2)该校学生估计该地今年(按 365 天计算)空 气质量达到优级别的天数约是 110 天,你知道他们是怎样估计出这个结论的?
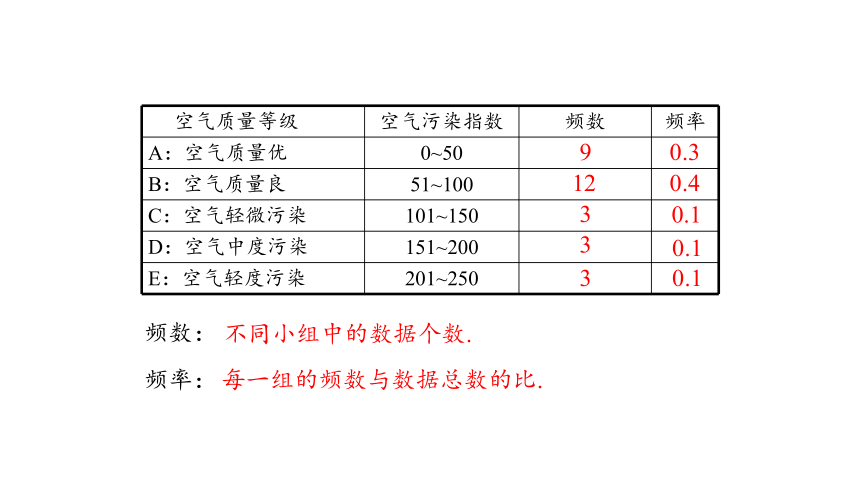
空气污 染指数 0~50 51~100 101~150 151~200 201~250
天 数 9 12 3 3 3
空气质量等级 空气污染指数 频数 频率
A:空气质量优 0~50
B:空气质量良 51~100
C:空气轻微污染 101~150
D:空气中度污染 151~200
E:空气轻度污染 201~250
频数:
不同小组中的数据个数.
频率:
每一组的频数与数据总数的比.
9
12
0.3
0.4
0.1
3
3
3
0.1
0.1
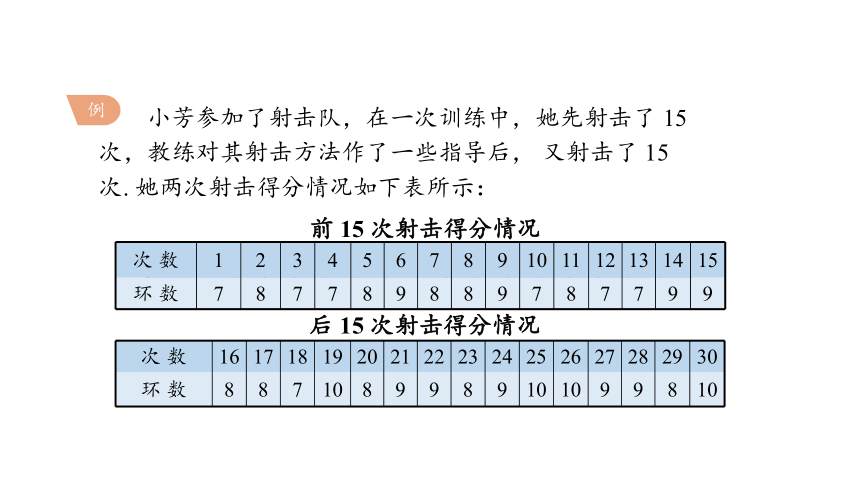
例
小芳参加了射击队,在一次训练中,她先射击了 15 次,教练对其射击方法作了一些指导后, 又射击了 15 次. 她两次射击得分情况如下表所示:
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
前 15 次射击得分情况
后 15 次射击得分情况
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
(1) 用表格表示小芳射击训练中前 15 次和后 15 次射击得分的频数和频率.
(2) 分别求出前 15 次和后 15 次射击得分的平均数(精确到 0.01),比较射击成绩的变化.
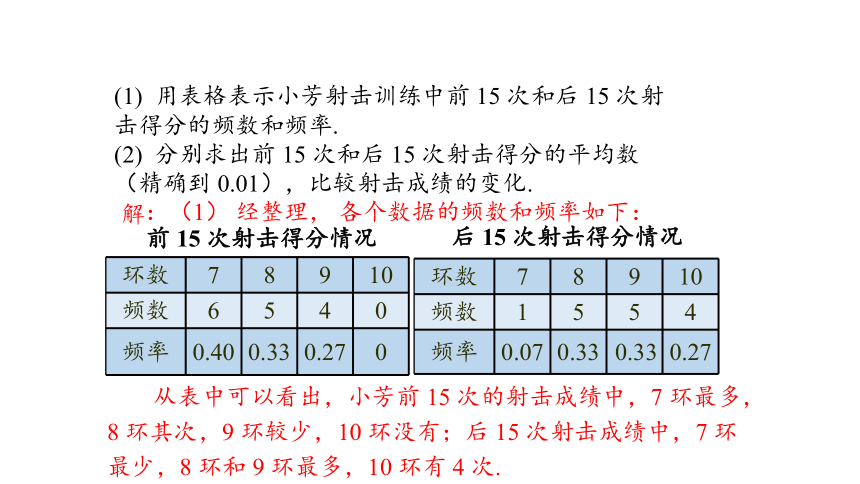
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
:(1) 经整理, 各个数据的频数和频率如下:
解
前 15 次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
0.33
后 15 次射击得分情况
从表中可以看出,小芳前 15 次的射击成绩中,7 环最多,8 环其次,9 环较少,10 环没有;后 15 次射击成绩中,7 环最少,8 环和 9 环最多,10 环有 4 次.
后 15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
(2) 前 15 次射击成绩的平均数是:
同理可求得后 15 次射击成绩的平均数约为 8.80.
与同桌同学合作,掷 10 次硬币,并把 10 次试验结果记录下来:
次数 1 2 3 4 5 6 7 8 9 10
结果 (正或反)
(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少, 它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少, 它们之间有什么关系?
做一做
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 正 反 反 反 正 反 反
出现“正面朝上” 的频数是 4,频率为 ;
出现“反面朝上”的频数是 6,频率为
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为 1.
假设某同学掷 10 次硬币的结果如下:
知识讲解
频数与频率的概念:
一般地,如果重复进行 n 次试验,某个试验结果出现的次数 m 称为在这 n 次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这 n 次试验中出现的频率.
随 堂 小 测
1.八一班的 40 名同学中,他们上学有的步行,有的骑自行车,还有骑电动车,据统计,骑自行车上学的频率为 40 %,则频数为( )
A.4 B.16 C.24 D.无法计算
B
2.在一次数学测试中,将某班40名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是( )
A.7 B.8 C.9 D.10
B
3.《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有40名学生,其中已经学会炒菜的学生频率是0.45,则该班学会炒菜的学生频数是________.
18
4.2015年7月31日,国际奥委会第128次全会在马来西亚吉隆坡举行,85位国际奥委会委员投票选择2022年冬奥会的举办城市,北京44票,阿拉木图40票,1票弃权,北京获得2022年冬季奥运会的举办权,北京得票的频率是________(精确到0.001).
0.518
5. “三年的初中学习生活快结束了,愿中考将我送达另一个理想的彼岸”,这 28 个汉字中,每个字的笔画数依次是 3,6,8,7,4,8,3,5,9,7,9,7,2,14,4,6,9,7,9,6,5,1,3,11,13,8,8,8,其中笔画数是 9 的字出现的频率是多少?
解:由题意得笔画数是 9 的字的频数为 4,
∴ 笔画数是 9 的字出现的频率是 4÷28=
6. 为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了不完整的统计图表:
整理情况 频数 频率
非常好 0.21
较好 70
一般
不好 36
请根据图表中提供的信息,解答下列问题.(1) 本次抽样共调查了多少名学生?
解:本次抽样共调查的学生数为: (名).
整理情况 频数 频率
非常好 0.21
较好 70
一般
不好 36
(2) 补全统计表中所缺的数据;
(3) 该校有 1500 名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共有多少名?
42
52
0.35
0.26
0.18
解:该校学生整理错题集情况“非常好”和“较好”的学生一共约有 1500×(0.21+0.35) = 840 (名).
小结
频数与频率
频数
频率
每一组的频数与数据总数的比
不同小组中的数据个数
频数与试验总次数的比
第5章 数据的频数分布
5.1 频数与频率
学习目标
1.通过实例和统计活动,感受频数和频率在各种实际问题中的具体涵义和共同本质,以形成关于频数(率)的一般概念,理解这些概念的意义和作用.
2.理解频数与频率之间的相互关系,会统计频数、计算频率.
3.认识频数分布是反映数据的分布,是对于数据的全面刻画.
4.了解频数、频率的一些简单实际应用,通过收集、分析数据的过程,初步作出合理的决策,提高处理问题、决策问题的能力.
学习重点、难点
对于频数、频率意义的理解.
重点:
难点:
对于重复试验理解其试验结果发生的频数、频率的意义.
课时导入
动脑筋
某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取 30 天的空气综合污染指数,数据如下:
国家环保总局公布的《空气质量级别表》
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 中度重污染 Ⅴ级
重度污染
(1)说说这 30 天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况);
(2)该校学生估计该地今年(按 365 天计算)空 气质量达到优级别的天数约是 110 天,你知道他们是怎样估计出这个结论的?
空气污 染指数 0~50 51~100 101~150 151~200 201~250
天 数 9 12 3 3 3
空气质量等级 空气污染指数 频数 频率
A:空气质量优 0~50
B:空气质量良 51~100
C:空气轻微污染 101~150
D:空气中度污染 151~200
E:空气轻度污染 201~250
频数:
不同小组中的数据个数.
频率:
每一组的频数与数据总数的比.
9
12
0.3
0.4
0.1
3
3
3
0.1
0.1
例
小芳参加了射击队,在一次训练中,她先射击了 15 次,教练对其射击方法作了一些指导后, 又射击了 15 次. 她两次射击得分情况如下表所示:
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
前 15 次射击得分情况
后 15 次射击得分情况
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
(1) 用表格表示小芳射击训练中前 15 次和后 15 次射击得分的频数和频率.
(2) 分别求出前 15 次和后 15 次射击得分的平均数(精确到 0.01),比较射击成绩的变化.
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
:(1) 经整理, 各个数据的频数和频率如下:
解
前 15 次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
0.33
后 15 次射击得分情况
从表中可以看出,小芳前 15 次的射击成绩中,7 环最多,8 环其次,9 环较少,10 环没有;后 15 次射击成绩中,7 环最少,8 环和 9 环最多,10 环有 4 次.
后 15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
(2) 前 15 次射击成绩的平均数是:
同理可求得后 15 次射击成绩的平均数约为 8.80.
与同桌同学合作,掷 10 次硬币,并把 10 次试验结果记录下来:
次数 1 2 3 4 5 6 7 8 9 10
结果 (正或反)
(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少, 它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少, 它们之间有什么关系?
做一做
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 正 反 反 反 正 反 反
出现“正面朝上” 的频数是 4,频率为 ;
出现“反面朝上”的频数是 6,频率为
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为 1.
假设某同学掷 10 次硬币的结果如下:
知识讲解
频数与频率的概念:
一般地,如果重复进行 n 次试验,某个试验结果出现的次数 m 称为在这 n 次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这 n 次试验中出现的频率.
随 堂 小 测
1.八一班的 40 名同学中,他们上学有的步行,有的骑自行车,还有骑电动车,据统计,骑自行车上学的频率为 40 %,则频数为( )
A.4 B.16 C.24 D.无法计算
B
2.在一次数学测试中,将某班40名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是( )
A.7 B.8 C.9 D.10
B
3.《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有40名学生,其中已经学会炒菜的学生频率是0.45,则该班学会炒菜的学生频数是________.
18
4.2015年7月31日,国际奥委会第128次全会在马来西亚吉隆坡举行,85位国际奥委会委员投票选择2022年冬奥会的举办城市,北京44票,阿拉木图40票,1票弃权,北京获得2022年冬季奥运会的举办权,北京得票的频率是________(精确到0.001).
0.518
5. “三年的初中学习生活快结束了,愿中考将我送达另一个理想的彼岸”,这 28 个汉字中,每个字的笔画数依次是 3,6,8,7,4,8,3,5,9,7,9,7,2,14,4,6,9,7,9,6,5,1,3,11,13,8,8,8,其中笔画数是 9 的字出现的频率是多少?
解:由题意得笔画数是 9 的字的频数为 4,
∴ 笔画数是 9 的字出现的频率是 4÷28=
6. 为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了不完整的统计图表:
整理情况 频数 频率
非常好 0.21
较好 70
一般
不好 36
请根据图表中提供的信息,解答下列问题.(1) 本次抽样共调查了多少名学生?
解:本次抽样共调查的学生数为: (名).
整理情况 频数 频率
非常好 0.21
较好 70
一般
不好 36
(2) 补全统计表中所缺的数据;
(3) 该校有 1500 名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共有多少名?
42
52
0.35
0.26
0.18
解:该校学生整理错题集情况“非常好”和“较好”的学生一共约有 1500×(0.21+0.35) = 840 (名).
小结
频数与频率
频数
频率
每一组的频数与数据总数的比
不同小组中的数据个数
频数与试验总次数的比
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
