19.2 一次函数同步测试题(含答案)
文档属性
| 名称 | 19.2 一次函数同步测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 783.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 23:23:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
19.2一次函数同步测试题
一、选择题(每小题3分,共30分)
1.下列函数中是的正比例函数的是( )
A. B. C. D.
2.下列函数中,是一次函数但不是正比例函数的为( )
A.y=- B.y=- C.y=- D.y=
3.关于函数,下列结论中,正确的是( )
A.函数图像经过点(1,3) B.函数图像经过二、四象限
C.y随x的增大而增大 D.不论x为何值,总有y>0
4.以下四点:(1,2),(2,3),(0,1),(-2,3)在直线y=2x+1上的有( )
A.1个 B.2个 C.3个 D.4个
5.一次函数y=-5x+3的图象经过的象限是( )
A.一、二、三 B.二、三、四 C.一、二、四 D.一、三、四
6.在同一直角坐标系中,对于函数:①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( )
A.通过点(-1,0)的是①和③ B.交点在y轴上的是②和④
C.相互平行的是①和③ D.关于x轴对称的是②和③
7.已知一次函数的图象与直线平行,且过点(8,2),则一次函数的解析式为( )
A. B. C. D.
8.已知一次函数图象上的三点,,,则,,的大小关系是
A. B. C. D.
9.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图像由线段和射线组成,则一次购买6千克这种苹果比分六次购买1千克这种苹果可节省的金额为( )
A.5 B.6 C.7 D.8
10.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是( )
A. B. C. D.且
二、填空题(每小题3分,共15分)
11.写出一个过点D(0,1)且y随x增大而减小的一次函数关系式为______________________.
12.如图,一次函数与轴,轴分别交于,两点,则不等式的解集是______.
13.已知方程组 的解为,则函数与的交点坐标为是 .
14.《九章算术》记载:今有坦高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺.问几何日相逢?意思是有一道墙,高9尺,上面种一株瓜,瓜蔓向下伸,每天长7寸;地上种着瓠向上长,每天长1尺,问瓜蔓、瓠蔓要多少天才相遇?如图是瓜蔓与瓠蔓离地面的高度(单位:尺)关于生长时间(单位:天)的函数图象,则由图可知两图象交点的横坐标是 .
15.如图,已知,,分别是的三条边长,,我们把关于的形如的一次函数称为“勾股一次函数”,若点在“勾股一次函数”的图象上,且的面积是5,则的值是 .
三、解答题(共75分)
16.(6分)已知一次函数y=(2a-3)x+4-b.根据下列条件,分别确定a,b的取值范围:
(1)函数值y随x的增大而增大;
(2)函数图象与y轴的交点在x轴下方;
(3)函数图象经过第二、三、四象限.
17.(6分)已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)判断点P(-1,1) 是否在这个一次函数的图象上;
(3)求此函数图象与x轴、y轴围成的三角形的面积.
18.(6分)画出函数的图象,利用图象:
(1)求方程的解;
(2)求不等式的解;
(3)若,求的取值范围.
19.(8分)如图,一次函数的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
20.(8分)如图所示,在同一个坐标系中一次函数和的图象,分别与轴交于点、,两直线交于点,已知点坐标为,点坐标为,观察图象并回答下列问题:
(1)关于的方程的解是 ;关于的不等式的解集是 ;
(2)直接写出关于的不等式组解集是 ;
(3)若点坐标为,关于的不等式的解集是 .
21.(9分)如图,在平面直角坐标系中,过点的直线与直线相交于点,动点沿路线运动.
(1)求直线的解析式.
(2)求的面积.
(3)当的面积是的面积的时,求出这时点的坐标.
22.(10分)如图所示,、表示某工厂甲、乙两车间生产的产量与所用时间(天之间的函数图象,根据图象回答:
(1)乙车间开始生产时,甲车间已生产了 ;
(2)甲车间每天生产 ,乙车间每天生产 ;
(3)从乙车间开始生产的第 天结束时,两车间生产的总产量相同;
(4)甲、乙两车间的产量与所用时间(天的函数关系式分别为 , ;
(5)第30天结束时,甲、乙两车间的总产量分别是 和 .
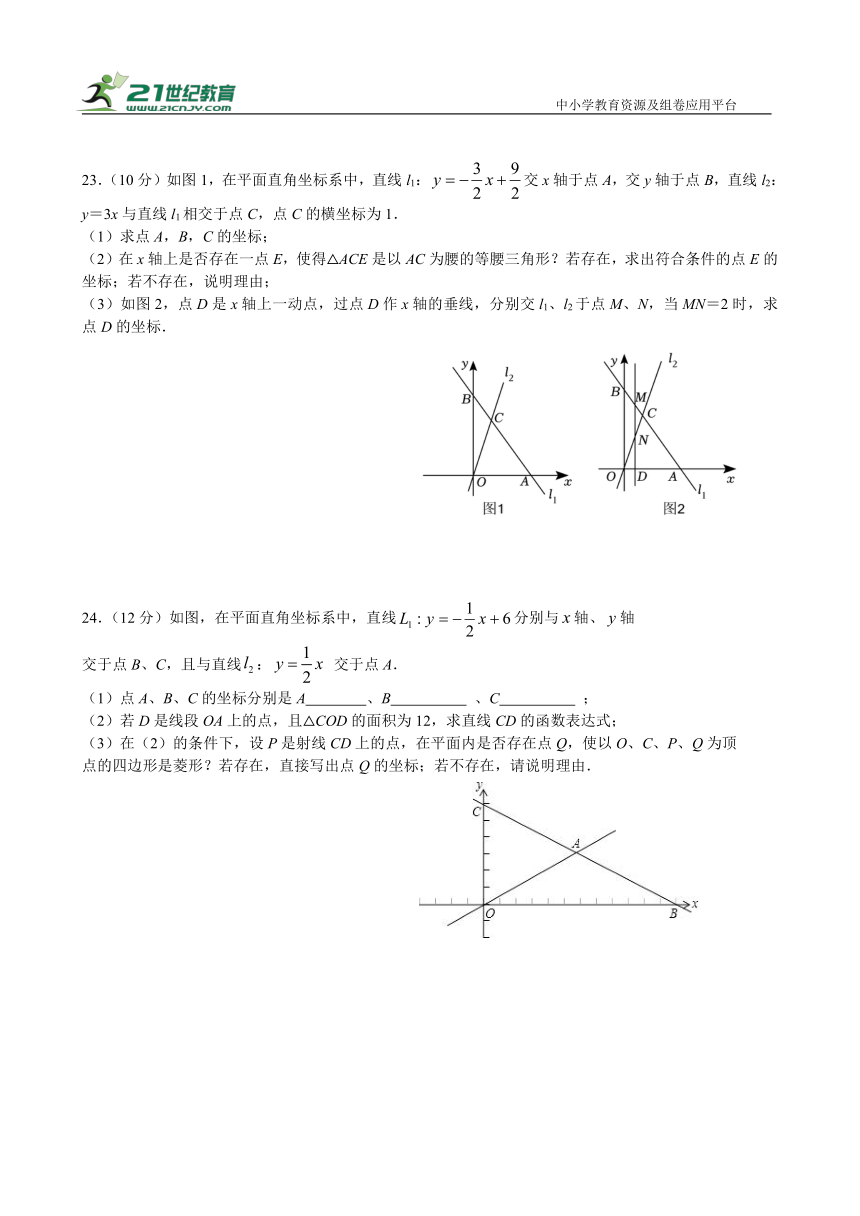
23.(10分)如图1,在平面直角坐标系中,直线l1:交x轴于点A,交y轴于点B,直线l2:y=3x与直线l1相交于点C,点C的横坐标为1.
(1)求点A,B,C的坐标;
(2)在x轴上是否存在一点E,使得△ACE是以AC为腰的等腰三角形?若存在,求出符合条件的点E的坐标;若不存在,说明理由;
(3)如图2,点D是x轴上一动点,过点D作x轴的垂线,分别交l1、l2于点M、N,当MN=2时,求点D的坐标.
24.(12分)如图,在平面直角坐标系中,直线分别与轴、轴
交于点B、C,且与直线: 交于点A.
(1)点A、B、C的坐标分别是A 、B 、C ;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶
点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
人教版八年级数学下册第19章一次函数19.2一次函数同步测试题
参考答案
一、选择题
1.C 2.C 3.C 4.A 5.C 6.C 7.C 8.A 9.D 解:设y关于x的函数关系式为,
当时,将、代入中,
,解得:,∴;
当时,将,代入中,
,解得:,
∴.
当时,,
当时,,
(元),故选D.
10.D解:∵,
∴当y=0时,x=;当x=0时,y=2t+2,
∴直线与x轴的交点坐标为(,0),与y轴的交点坐标为(0,2t+2),
∵t>0,
∴2t+2>2,
当t=时,2t+2=3,此时=-6,由图象知:直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图1,
当t=2时,2t+2=6,此时=-3,由图象知:直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图2,
当t=1时,2t+2=4,=-4,由图象知:直线()与两坐标轴围成的三角形区域(不含边界)中有且只有三个整点,如图3,
∴且,
故选:D.
二、填空题
11.(答案不唯一) 12. 13.(-1,1) 14.解:7寸尺.
瓜蔓在高9尺的墙上,向下伸,每天长7寸,
天时瓜蔓的高度.
地上种着瓠向上长,每天长1尺,
天时高度.
相遇时高度相等,
.
, .
两图象交点的横坐标为.
15.5 解:点在“勾股一次函数” 的图象上,
,即,
又,,分别是的三条边长,,的面积是5,
,即,
又,
,
即,
解得,
三、解答题
16.解:(1)因为k>0时,函数y随x的增大而增大,
可得:2a-3>0,
解得:a>1.5,b为任意实数;
(2)因为4-b<0,2a-3≠0时,函数图象与y轴的交点在x轴下方,
解得:b>4,a≠1.5,
所以函数图象与y轴的交点在x轴下方时,b>4,a≠1.5;
(3)因为2a-3<0,4-b<0时,函数图象经过第二、三、四象限,
解得:a<1.5,b>4,
所以函数图象经过第二、三、四象限,a<1.5,b>4..
17.解:(1)设这个一次函数的解析式为
∵y=kx+b的图象过点(-2,-3)与(1, 3)
∴ 解方程组得
∴这个一次函数的解析式为y=2x+1
(2)∵当x=-1时,y=2×(-1)+1≠1
∴点P(-1,1)不在y=2x+1的图象上.
(3)由一次函数的解析式y=2x+1可得,图象与x轴,y轴的交点分别为(,0),(0,1)
∴此函数图象与x轴、y轴围成的三角形的面积为:
18.依题意得:
x 0 -3
y 6 0
由图像得(1)x=-3;
(2)x>-3;
(3).
19.(1)解:一次函数中,
令x=0得:y=2;令y=0,解得x=3.
则A的坐标是(0,2),C的坐标是(3,0).
作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
又∵AB=AC,∠BOA=∠CDA=90°,
∴△ABO≌△CAD,
∴AD=OB=2,CD=OA=3,OD=OA+AD=5.
则C的坐标是(5,3).
设BC的解析式是y=kx+b,
根据题意得:,解得:.
则BC的解析式是:;
20.解:(1)一次函数和的图象,分别与轴交于点、点,
关于的方程的解是,
关于的不等式的解集是;
故答案为:.
(2)根据图象可得关于的不等式组解集为;
故答案为:.
(3)点,
结合图象可知,不等式的解集是.
故答案为:.
21.解:(1)设直线的解析式是,
根据题意得:,解得:,
则直线的解析式是:;
(2)在中,令,解得:,
;
(3)设的解析式是,则,
解得:,
则直线的解析式是:,
当的面积是的面积的时,
的横坐标是,
在中,当时,,则的坐标是;
在中,则,则的坐标是.
则的坐标是:或.
22.解:(1)400;
(2)10,20;
(3)20;
(4)设,因为图象过和,
所以,解得.
所以;
设,因为图象过、,
所以,,所以;
(5)当时,;.
23.解:(1)当x=1时,y=3x=3
∴C(1,3)
当x=0时,得
∴B(0,)
令,得x=3
∴A(3,0)
(2)存在.理由如下:
如图1,过C作CF⊥x,则F(1,0)
∴AF=3-1=2,CF=3
∴AC=
当AE=AC=时,OE=3+或-3
∴E(3+,0)或(3-,0)
当CA=CE时,则AF=EF=2
∴OE=2-1=1
∴E(-1,0)
(3)如图,设M(t,),则N(t,3t),D(t,0)
∴MN=-3t=2或3t-()=2
解得t=或
∴D(,0)或(,0)
24.(1)A(6,3),B(12,0),C(0,6).
(2)解:设D,
∵△COD的面积为12,
∴,解得:,
∴D(4,2),
设直线CD的函数表达式是,
把C(0,6),D(4,2)代入得:
解得:
∴,
答:直线CD的函数表达式是.
(3)答:存在点Q,使以O、C、P、Q为顶点的四边形是菱形,点Q的坐标是
(6,6)或(-3,3)或.
19.2一次函数同步测试题
一、选择题(每小题3分,共30分)
1.下列函数中是的正比例函数的是( )
A. B. C. D.
2.下列函数中,是一次函数但不是正比例函数的为( )
A.y=- B.y=- C.y=- D.y=
3.关于函数,下列结论中,正确的是( )
A.函数图像经过点(1,3) B.函数图像经过二、四象限
C.y随x的增大而增大 D.不论x为何值,总有y>0
4.以下四点:(1,2),(2,3),(0,1),(-2,3)在直线y=2x+1上的有( )
A.1个 B.2个 C.3个 D.4个
5.一次函数y=-5x+3的图象经过的象限是( )
A.一、二、三 B.二、三、四 C.一、二、四 D.一、三、四
6.在同一直角坐标系中,对于函数:①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( )
A.通过点(-1,0)的是①和③ B.交点在y轴上的是②和④
C.相互平行的是①和③ D.关于x轴对称的是②和③
7.已知一次函数的图象与直线平行,且过点(8,2),则一次函数的解析式为( )
A. B. C. D.
8.已知一次函数图象上的三点,,,则,,的大小关系是
A. B. C. D.
9.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图像由线段和射线组成,则一次购买6千克这种苹果比分六次购买1千克这种苹果可节省的金额为( )
A.5 B.6 C.7 D.8
10.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是( )
A. B. C. D.且
二、填空题(每小题3分,共15分)
11.写出一个过点D(0,1)且y随x增大而减小的一次函数关系式为______________________.
12.如图,一次函数与轴,轴分别交于,两点,则不等式的解集是______.
13.已知方程组 的解为,则函数与的交点坐标为是 .
14.《九章算术》记载:今有坦高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺.问几何日相逢?意思是有一道墙,高9尺,上面种一株瓜,瓜蔓向下伸,每天长7寸;地上种着瓠向上长,每天长1尺,问瓜蔓、瓠蔓要多少天才相遇?如图是瓜蔓与瓠蔓离地面的高度(单位:尺)关于生长时间(单位:天)的函数图象,则由图可知两图象交点的横坐标是 .
15.如图,已知,,分别是的三条边长,,我们把关于的形如的一次函数称为“勾股一次函数”,若点在“勾股一次函数”的图象上,且的面积是5,则的值是 .
三、解答题(共75分)
16.(6分)已知一次函数y=(2a-3)x+4-b.根据下列条件,分别确定a,b的取值范围:
(1)函数值y随x的增大而增大;
(2)函数图象与y轴的交点在x轴下方;
(3)函数图象经过第二、三、四象限.
17.(6分)已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)判断点P(-1,1) 是否在这个一次函数的图象上;
(3)求此函数图象与x轴、y轴围成的三角形的面积.
18.(6分)画出函数的图象,利用图象:
(1)求方程的解;
(2)求不等式的解;
(3)若,求的取值范围.
19.(8分)如图,一次函数的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
20.(8分)如图所示,在同一个坐标系中一次函数和的图象,分别与轴交于点、,两直线交于点,已知点坐标为,点坐标为,观察图象并回答下列问题:
(1)关于的方程的解是 ;关于的不等式的解集是 ;
(2)直接写出关于的不等式组解集是 ;
(3)若点坐标为,关于的不等式的解集是 .
21.(9分)如图,在平面直角坐标系中,过点的直线与直线相交于点,动点沿路线运动.
(1)求直线的解析式.
(2)求的面积.
(3)当的面积是的面积的时,求出这时点的坐标.
22.(10分)如图所示,、表示某工厂甲、乙两车间生产的产量与所用时间(天之间的函数图象,根据图象回答:
(1)乙车间开始生产时,甲车间已生产了 ;
(2)甲车间每天生产 ,乙车间每天生产 ;
(3)从乙车间开始生产的第 天结束时,两车间生产的总产量相同;
(4)甲、乙两车间的产量与所用时间(天的函数关系式分别为 , ;
(5)第30天结束时,甲、乙两车间的总产量分别是 和 .
23.(10分)如图1,在平面直角坐标系中,直线l1:交x轴于点A,交y轴于点B,直线l2:y=3x与直线l1相交于点C,点C的横坐标为1.
(1)求点A,B,C的坐标;
(2)在x轴上是否存在一点E,使得△ACE是以AC为腰的等腰三角形?若存在,求出符合条件的点E的坐标;若不存在,说明理由;
(3)如图2,点D是x轴上一动点,过点D作x轴的垂线,分别交l1、l2于点M、N,当MN=2时,求点D的坐标.
24.(12分)如图,在平面直角坐标系中,直线分别与轴、轴
交于点B、C,且与直线: 交于点A.
(1)点A、B、C的坐标分别是A 、B 、C ;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶
点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
人教版八年级数学下册第19章一次函数19.2一次函数同步测试题
参考答案
一、选择题
1.C 2.C 3.C 4.A 5.C 6.C 7.C 8.A 9.D 解:设y关于x的函数关系式为,
当时,将、代入中,
,解得:,∴;
当时,将,代入中,
,解得:,
∴.
当时,,
当时,,
(元),故选D.
10.D解:∵,
∴当y=0时,x=;当x=0时,y=2t+2,
∴直线与x轴的交点坐标为(,0),与y轴的交点坐标为(0,2t+2),
∵t>0,
∴2t+2>2,
当t=时,2t+2=3,此时=-6,由图象知:直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图1,
当t=2时,2t+2=6,此时=-3,由图象知:直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图2,
当t=1时,2t+2=4,=-4,由图象知:直线()与两坐标轴围成的三角形区域(不含边界)中有且只有三个整点,如图3,
∴且,
故选:D.
二、填空题
11.(答案不唯一) 12. 13.(-1,1) 14.解:7寸尺.
瓜蔓在高9尺的墙上,向下伸,每天长7寸,
天时瓜蔓的高度.
地上种着瓠向上长,每天长1尺,
天时高度.
相遇时高度相等,
.
, .
两图象交点的横坐标为.
15.5 解:点在“勾股一次函数” 的图象上,
,即,
又,,分别是的三条边长,,的面积是5,
,即,
又,
,
即,
解得,
三、解答题
16.解:(1)因为k>0时,函数y随x的增大而增大,
可得:2a-3>0,
解得:a>1.5,b为任意实数;
(2)因为4-b<0,2a-3≠0时,函数图象与y轴的交点在x轴下方,
解得:b>4,a≠1.5,
所以函数图象与y轴的交点在x轴下方时,b>4,a≠1.5;
(3)因为2a-3<0,4-b<0时,函数图象经过第二、三、四象限,
解得:a<1.5,b>4,
所以函数图象经过第二、三、四象限,a<1.5,b>4..
17.解:(1)设这个一次函数的解析式为
∵y=kx+b的图象过点(-2,-3)与(1, 3)
∴ 解方程组得
∴这个一次函数的解析式为y=2x+1
(2)∵当x=-1时,y=2×(-1)+1≠1
∴点P(-1,1)不在y=2x+1的图象上.
(3)由一次函数的解析式y=2x+1可得,图象与x轴,y轴的交点分别为(,0),(0,1)
∴此函数图象与x轴、y轴围成的三角形的面积为:
18.依题意得:
x 0 -3
y 6 0
由图像得(1)x=-3;
(2)x>-3;
(3).
19.(1)解:一次函数中,
令x=0得:y=2;令y=0,解得x=3.
则A的坐标是(0,2),C的坐标是(3,0).
作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
又∵AB=AC,∠BOA=∠CDA=90°,
∴△ABO≌△CAD,
∴AD=OB=2,CD=OA=3,OD=OA+AD=5.
则C的坐标是(5,3).
设BC的解析式是y=kx+b,
根据题意得:,解得:.
则BC的解析式是:;
20.解:(1)一次函数和的图象,分别与轴交于点、点,
关于的方程的解是,
关于的不等式的解集是;
故答案为:.
(2)根据图象可得关于的不等式组解集为;
故答案为:.
(3)点,
结合图象可知,不等式的解集是.
故答案为:.
21.解:(1)设直线的解析式是,
根据题意得:,解得:,
则直线的解析式是:;
(2)在中,令,解得:,
;
(3)设的解析式是,则,
解得:,
则直线的解析式是:,
当的面积是的面积的时,
的横坐标是,
在中,当时,,则的坐标是;
在中,则,则的坐标是.
则的坐标是:或.
22.解:(1)400;
(2)10,20;
(3)20;
(4)设,因为图象过和,
所以,解得.
所以;
设,因为图象过、,
所以,,所以;
(5)当时,;.
23.解:(1)当x=1时,y=3x=3
∴C(1,3)
当x=0时,得
∴B(0,)
令,得x=3
∴A(3,0)
(2)存在.理由如下:
如图1,过C作CF⊥x,则F(1,0)
∴AF=3-1=2,CF=3
∴AC=
当AE=AC=时,OE=3+或-3
∴E(3+,0)或(3-,0)
当CA=CE时,则AF=EF=2
∴OE=2-1=1
∴E(-1,0)
(3)如图,设M(t,),则N(t,3t),D(t,0)
∴MN=-3t=2或3t-()=2
解得t=或
∴D(,0)或(,0)
24.(1)A(6,3),B(12,0),C(0,6).
(2)解:设D,
∵△COD的面积为12,
∴,解得:,
∴D(4,2),
设直线CD的函数表达式是,
把C(0,6),D(4,2)代入得:
解得:
∴,
答:直线CD的函数表达式是.
(3)答:存在点Q,使以O、C、P、Q为顶点的四边形是菱形,点Q的坐标是
(6,6)或(-3,3)或.
