六年级数学下册苏教版4.7探索规律:面积的变化课件(共18张PPT)
文档属性
| 名称 | 六年级数学下册苏教版4.7探索规律:面积的变化课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 991.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 06:51:15 | ||
图片预览



文档简介
(共18张PPT)
苏教版小学数学六年级下册
4.7探索规律:面积的变化
学习目标
1、使学生在探究规律的过程中,自主探究出图形
放大后和放大前对应的边长比与面积比之间的关系。
2、经历量一量、估一估、算一算等活动,积累数学
活动的经验,培养观察综合、归纳推理的能力。
3、在探究面积变化规律的过程中获得成功的体验,
体会数学规律的奇妙,增强学好数学的信心。
学习重点:图形放大后和放大前对应边比与面积比之间的关系。
学习难点:立体图形放大后和放大前对应边比与体积比之间的关系。
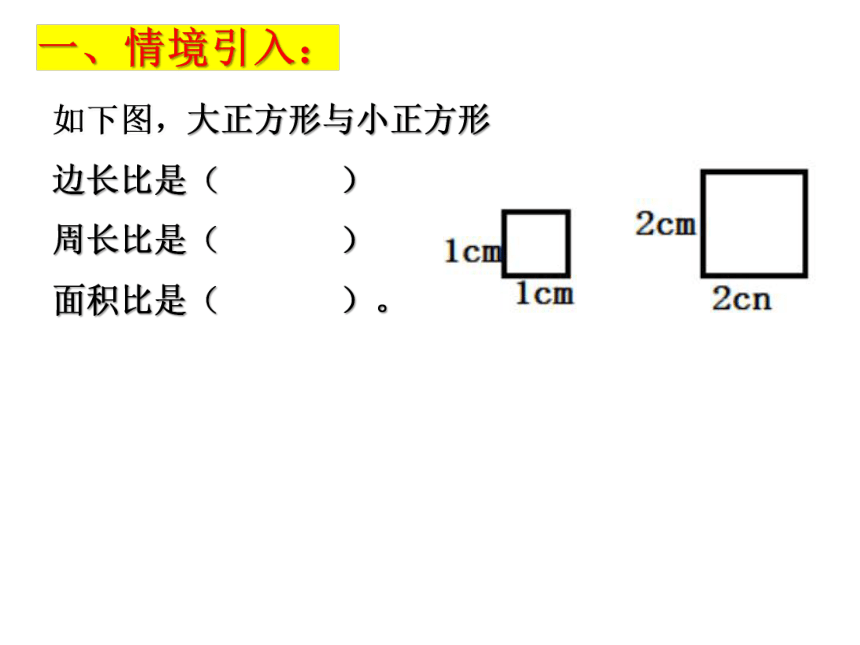
一、情境引入:
如下图,大正方形与小正方形
边长比是( )
周长比是( )
面积比是( )。
探究新知
1、操作比较:
问题:右面的大长方形是小长方形按比例放大后得到的。分别量出它们的长和宽,写出对应边长的比。
大长方形与小长方形长的比是( ):( ),
宽的比是( ):( )。
3cm
1cm
3cm
9cm
9 3
3 1
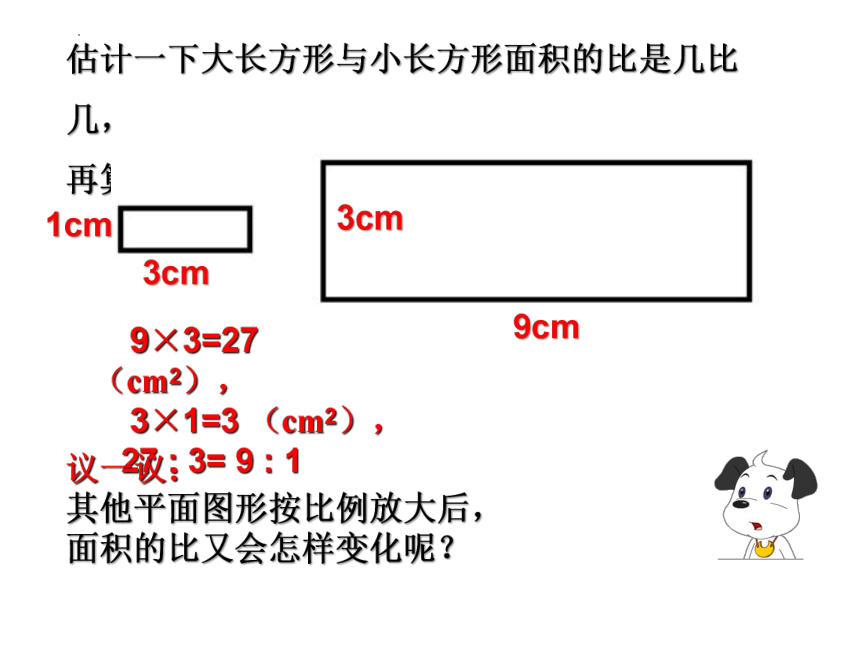
估计一下大长方形与小长方形面积的比是几比几,
再算一算,看看你估计得对不对。
3cm
1cm
3cm
9cm
9×3=27(cm2),
3×1=3 (cm2),
27 : 3= 9 : 1
议一议:
其他平面图形按比例放大后,
面积的比又会怎样变化呢?
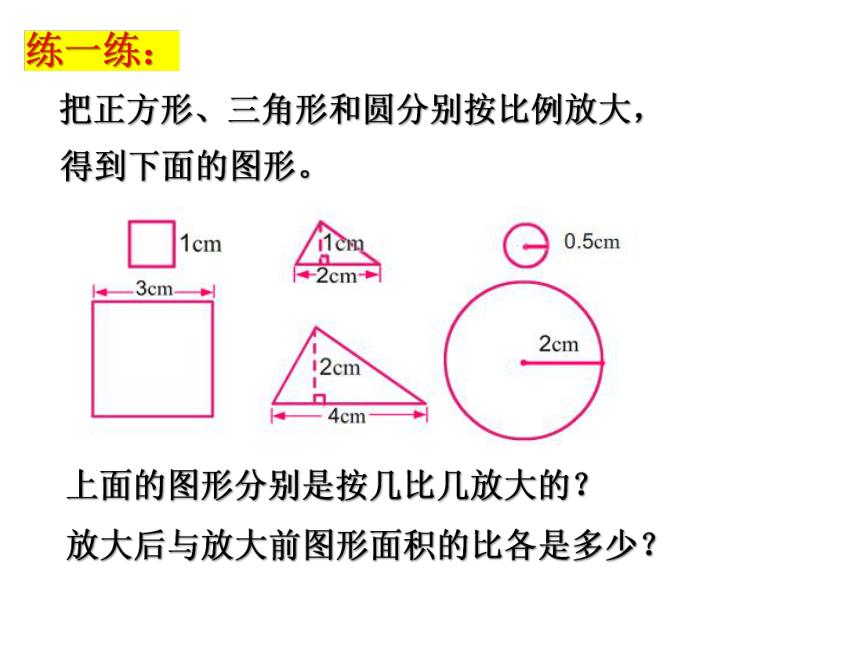
练一练:
把正方形、三角形和圆分别按比例放大,
得到下面的图形。
上面的图形分别是按几比几放大的?
放大后与放大前图形面积的比各是多少?
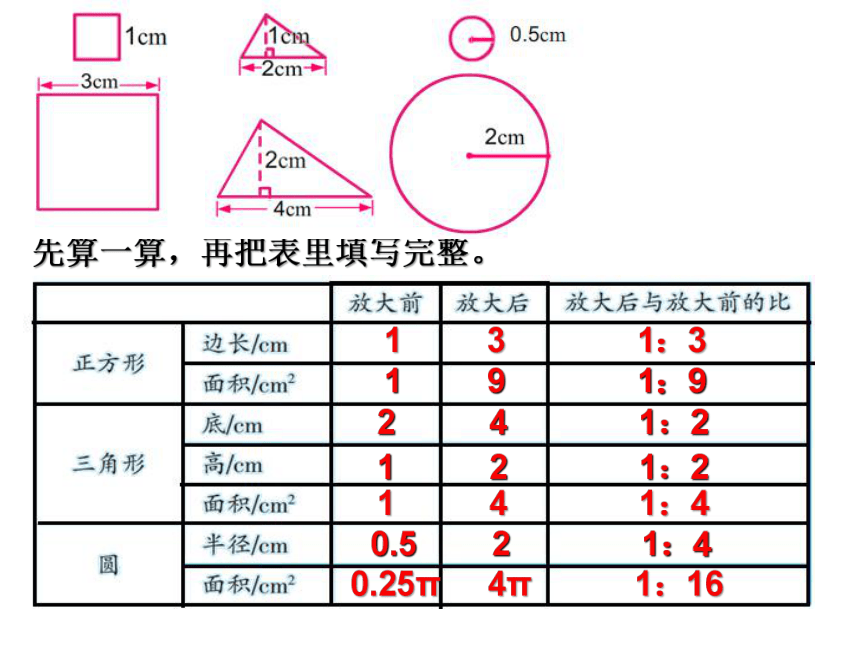
先算一算,再把表里填写完整。
1 3 1:3
1 9 1:9
2 4 1:2
1 2 1:2
1 4 1:4
0.5 2 1:4
0.25π 4π 1:16
比较每个图形放大后与放大前的长度比和面积比,你能发现什么规律?
发现:
长度比是2 :1, 面积比是4 : 1;
长度比是3 : 1,面积比是 9 : 1……
结论:
两个比的后项都是1,面积比的前项
是长度比前项的平方。
如果把一个图形按 n︰1 的比放大,放大后与放大前图形的面积比是( )。
n2︰1
二、例题讲解:
例1、把一块长与宽的比是7:2的长方形的土地
画在比例尺是1:500的图纸上,长方形的周长是36厘米,求这块长方形土地的实际面积。
例2、长方体、正方体等按比例放大后,
体积比和长度比会有什么关系?
(1)把长方体、正方体等按比例放大后分别
按比例放大,得到下面的图形。
大、小正方体的棱长比是( ),
底面积比是( ),表面积比是( ),
体积比是( );
大、小长方体方体的长之比是( ),
宽之比是( ),高之比是( ),
底面积比是( ) ,表面积比是( ),
体积比是( )。
小结:
如果把一个几何体按 n︰1 的比放大,
放大后与放大前图形的体积比是( )。
1、如图,将平行四边形ABCD按一定的比例放大得到平行四边形AEFG,并且AB=BE,下面说法
错误的是( )。
A、AG=2AD
B、EF=2BC
C、周长扩大到原来的2倍
D、面积扩大到原来的2倍
三、基础强化:
2、若一幅建筑施工图的比例尺为1:1000,这个施工图的图上面积与实际面积是( );
若图上面积是20平方厘米,则实际面积是( )平方米。
3、两个圆的半径分别是6厘米和9厘米,那么
它们的半径比是( ),周长比是( ),
面积比是( ),
4、将一个圆先按1:2的比缩小,再按3:1的比放大,这个圆现在的面积是原来的( )。
A、 B、 C、 D、
5、把一个三角形按2:1的比放大,已知放大后
三角形的底是14厘米,面积是140平方厘米,
放大前三角形的高是多少厘米?
四、拓展提高:
6、将一个小圆放大成一个大圆,它们的面积差
是209平方厘米,小圆与大圆的直径比是9:10,
求小圆的面积。
五、总结反思:
1、如果把一个图形按 n︰1 的比放大,放大后
与放大前图形的面积比是( )︰( )。
2、如果把一个立体图形按 n︰1 的比放大,
放大后与放大前图形的体积比是( )︰( )。
六、随堂检测:
1、将高是100米、面积是5000平方米的梯形按1:2000的比缩小,新的梯形面积是多少平方厘米?
2、把一个半径为1厘米圆放大成一个大圆,
大圆的面积是12.56平方厘米,则原来圆是
按( ):1放大的。
苏教版小学数学六年级下册
4.7探索规律:面积的变化
学习目标
1、使学生在探究规律的过程中,自主探究出图形
放大后和放大前对应的边长比与面积比之间的关系。
2、经历量一量、估一估、算一算等活动,积累数学
活动的经验,培养观察综合、归纳推理的能力。
3、在探究面积变化规律的过程中获得成功的体验,
体会数学规律的奇妙,增强学好数学的信心。
学习重点:图形放大后和放大前对应边比与面积比之间的关系。
学习难点:立体图形放大后和放大前对应边比与体积比之间的关系。
一、情境引入:
如下图,大正方形与小正方形
边长比是( )
周长比是( )
面积比是( )。
探究新知
1、操作比较:
问题:右面的大长方形是小长方形按比例放大后得到的。分别量出它们的长和宽,写出对应边长的比。
大长方形与小长方形长的比是( ):( ),
宽的比是( ):( )。
3cm
1cm
3cm
9cm
9 3
3 1
估计一下大长方形与小长方形面积的比是几比几,
再算一算,看看你估计得对不对。
3cm
1cm
3cm
9cm
9×3=27(cm2),
3×1=3 (cm2),
27 : 3= 9 : 1
议一议:
其他平面图形按比例放大后,
面积的比又会怎样变化呢?
练一练:
把正方形、三角形和圆分别按比例放大,
得到下面的图形。
上面的图形分别是按几比几放大的?
放大后与放大前图形面积的比各是多少?
先算一算,再把表里填写完整。
1 3 1:3
1 9 1:9
2 4 1:2
1 2 1:2
1 4 1:4
0.5 2 1:4
0.25π 4π 1:16
比较每个图形放大后与放大前的长度比和面积比,你能发现什么规律?
发现:
长度比是2 :1, 面积比是4 : 1;
长度比是3 : 1,面积比是 9 : 1……
结论:
两个比的后项都是1,面积比的前项
是长度比前项的平方。
如果把一个图形按 n︰1 的比放大,放大后与放大前图形的面积比是( )。
n2︰1
二、例题讲解:
例1、把一块长与宽的比是7:2的长方形的土地
画在比例尺是1:500的图纸上,长方形的周长是36厘米,求这块长方形土地的实际面积。
例2、长方体、正方体等按比例放大后,
体积比和长度比会有什么关系?
(1)把长方体、正方体等按比例放大后分别
按比例放大,得到下面的图形。
大、小正方体的棱长比是( ),
底面积比是( ),表面积比是( ),
体积比是( );
大、小长方体方体的长之比是( ),
宽之比是( ),高之比是( ),
底面积比是( ) ,表面积比是( ),
体积比是( )。
小结:
如果把一个几何体按 n︰1 的比放大,
放大后与放大前图形的体积比是( )。
1、如图,将平行四边形ABCD按一定的比例放大得到平行四边形AEFG,并且AB=BE,下面说法
错误的是( )。
A、AG=2AD
B、EF=2BC
C、周长扩大到原来的2倍
D、面积扩大到原来的2倍
三、基础强化:
2、若一幅建筑施工图的比例尺为1:1000,这个施工图的图上面积与实际面积是( );
若图上面积是20平方厘米,则实际面积是( )平方米。
3、两个圆的半径分别是6厘米和9厘米,那么
它们的半径比是( ),周长比是( ),
面积比是( ),
4、将一个圆先按1:2的比缩小,再按3:1的比放大,这个圆现在的面积是原来的( )。
A、 B、 C、 D、
5、把一个三角形按2:1的比放大,已知放大后
三角形的底是14厘米,面积是140平方厘米,
放大前三角形的高是多少厘米?
四、拓展提高:
6、将一个小圆放大成一个大圆,它们的面积差
是209平方厘米,小圆与大圆的直径比是9:10,
求小圆的面积。
五、总结反思:
1、如果把一个图形按 n︰1 的比放大,放大后
与放大前图形的面积比是( )︰( )。
2、如果把一个立体图形按 n︰1 的比放大,
放大后与放大前图形的体积比是( )︰( )。
六、随堂检测:
1、将高是100米、面积是5000平方米的梯形按1:2000的比缩小,新的梯形面积是多少平方厘米?
2、把一个半径为1厘米圆放大成一个大圆,
大圆的面积是12.56平方厘米,则原来圆是
按( ):1放大的。
