九年级数学下册试题 第27章《圆与正方形》单元复习卷-沪教版(含解析)
文档属性
| 名称 | 九年级数学下册试题 第27章《圆与正方形》单元复习卷-沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 988.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 16:42:25 | ||
图片预览



文档简介
第27章《圆与正方形》单元复习卷
一、选择题:本题共10个小题,每小题3分,共30分。
1.半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,-4)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
2.一直角三角形的斜边长为c,其内切圆半径是r,则三角形面积与其内切圆的面积之比是( )
A. B. C. D.
3.如图,P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,,,则线段OP的长为( )
A.6 B.4 C.4 D.8
4.如图,要拧开一个边长为a=8mm的正六边形螺帽,扳手张开的开口b至少为( )
A.8mm B.16mm C.8mm D.4mm
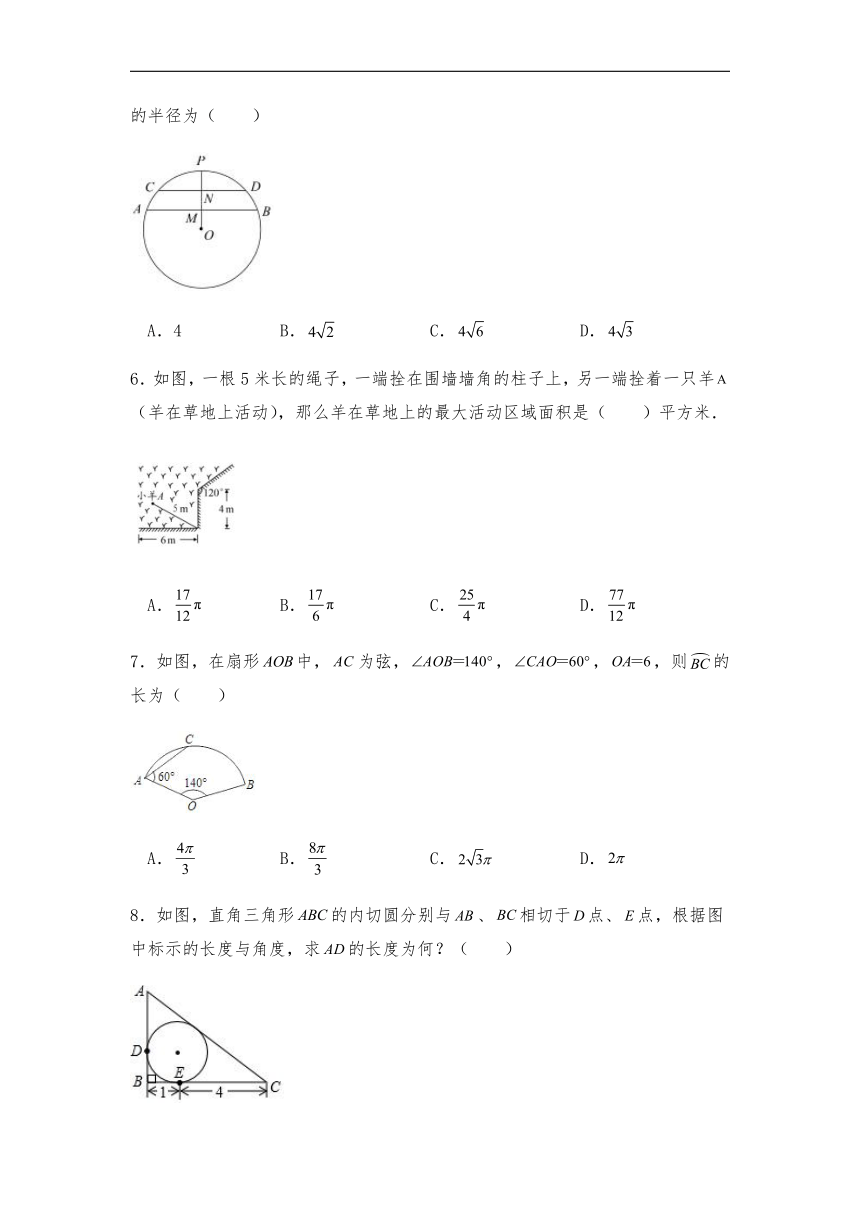
5.如图,在中,弦,,,,,则的半径为( )
A.4 B. C. D.
6.如图,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊(羊在草地上活动),那么羊在草地上的最大活动区域面积是( )平方米.
A. B. C. D.
7.如图,在扇形中,为弦,,,,则的长为( )
A. B. C. D.
8.如图,直角三角形的内切圆分别与、相切于点、点,根据图中标示的长度与角度,求的长度为何?( )
A. B. C. D.
9.如图,在菱形中,点是的中点,以为圆心、为半径作弧,交于点,连接.若,,则阴影部分的面积为( )
A. B. C. D.
10.如图,正方形的边长为4,点在边上运动,点在边上运动,运动过程中的长度保持不变,且.若是的中点,是边上的动点,则的最小值为( )
A. B. C. D.
二、填空题:本题共8个小题,每题3分,共24分。
11.已知圆O的面积为,若点P在圆上,则______.
12.若一个扇形的弧长为2πcm,面积为2πcm2,则这个扇形的半径为______cm.
13.在⊙O 中,弦 AB 所对圆心角为 140°,则弦AB 所对的圆周角的度数是___________.
14.如图,为了美化校园,学校在一块靠墙角的空地上建造了一个扇形花圃,其圆心角AOB=120°,半径为6m,则扇形的弧长是_________m.(结果保留)
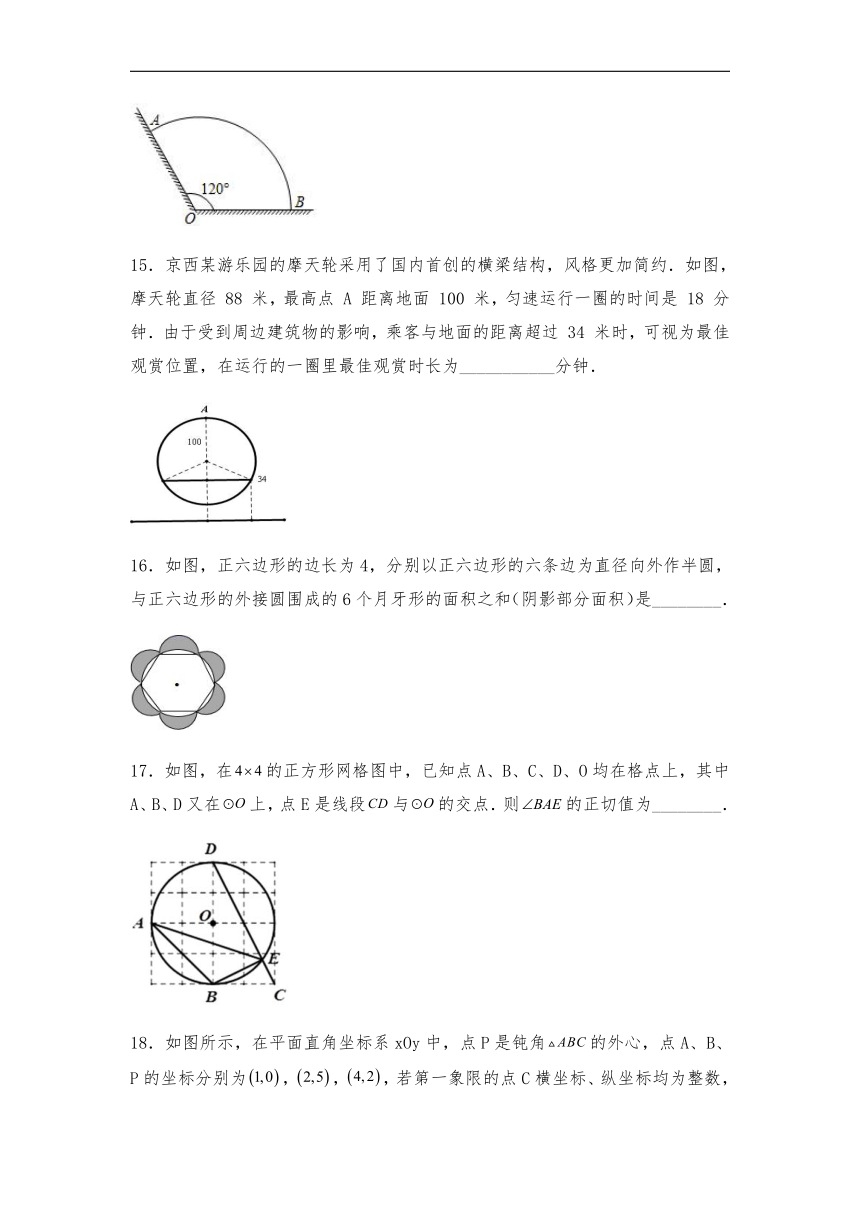
15.京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约.如图,摩天轮直径 88 米,最高点 A 距离地面 100 米,匀速运行一圈的时间是 18 分钟.由于受到周边建筑物的影响,乘客与地面的距离超过 34 米时,可视为最佳观赏位置,在运行的一圈里最佳观赏时长为___________分钟.
16.如图,正六边形的边长为4,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是________.
17.如图,在的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在上,点E是线段与的交点.则的正切值为________.
18.如图所示,在平面直角坐标系xOy中,点P是钝角的外心,点A、B、P的坐标分别为,,,若第一象限的点C横坐标、纵坐标均为整数,则点C的坐标为______.
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD⊥BC于点E.
(1)求证:∠BAD=∠CAD;
(2)连接BO并延长,交AC于点F,交⊙O于点G,连接GC若OE=3,∠CBG=30°,求的长.
20.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A,B重合),连接AP,BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP.
21.如图,已知,在ABC中,O为AB上一点,CO平分∠ACB,以O为圆心,OB长为半径作⊙O,⊙O与BC相切于点B,交CO于点D,延长CO交⊙O于点E,连接BD,BE.
(1)求证:AC是⊙O的切线.
(2)若tan∠BDE,BC=6,求⊙O的半径.
22.如图,已知内接干,是的直径,的平分线交于点,交于点,连接,作,交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径和的长.
23.如图,在⊙中,是直径,,垂足为P,过点的的切线与的延长线交于点, 连接.
(1)求证:为⊙的切线;
(2)若⊙半径为3,,求.
24.如图,点为以为直径的半圆的圆心,点,在直径上,点,在上,四边形为正方形,点在上运动(点与点,不重合),连接并延长交的延长线于点,连接交于点,连接.
(1)求的值;
(2)求的值;
(3)令,,直径(,是常数),求关于的函数解析式,并指明自变量的取值范围.
25.如图,已知,是的直径,,与的边,分别交于点,,连接并延长,与的延长线交于点,.
(1)求证:是的切线;
(2)若,求的值;
(3)在(2)的条件下,若的平分线交于点,连接交于点,求的值.
答案
一、选择题。
1.A
【分析】由题意先利用两点间的距离公式求出点P到原点的距离OP,再判断OP与半径r的大小关系,从而得出答案.
【详解】解:∵圆心P的坐标为(3,-4),
∴,
∵⊙P的半径为5,
∴原点O在⊙P上.
故选:A.
2.B
【分析】先画出示意图,然后连接内心和直角三角形的各个顶点,设直角三角形的两条直角边是a,b,则直角三角形的面积是,再根据正方形的判定与性质以及切线长定理可得,由此可得直角三角形的面积是,最后再结合内切圆的面积是即可求得答案.
【详解】解:如图,在中,∠C=90°,AB=c,⊙O为的内切圆,切点分别为点D、E、F,连接OA、OB、OC、OD、OE、OF,
设直角三角形的两条直角边分别为,,
∵⊙O为的内切圆,切点分别为点D、E、F,
∴
∴
,
∵
∴四边形ODCE为正方形,
∴,
∴,,
∵⊙O为的内切圆,切点分别为点D、E、F,
∴
∵,
∴,
,
∴,
又,
.
故选:B.
3.D
【分析】连接,通过直角三角形的性质求解即可.
【详解】解:连接,
∴,
∵PA为⊙O的切线,A为切点,
∴∠OAP=90°,
∵,
∴OP=2OA=8,
故选D.
4.C
【分析】由题意设正六边形的中心是O,其一边是AB,连接OA、OB、OC、AC,OB交AC于M,则∠AOB=∠BOC=60°,得出OA=OB=AB=OC=BC,则四边形ABCO是菱形,得出AC⊥OB,AM=CM,由sin∠AOB=,进而计算即可得出结果.
【详解】解:设正六边形的中心是O,其一边是AB,连接OA、OB、OC、AC,OB交AC于M,如图所示:
∴∠AOB=∠BOC=60°,OA=OB=OC
∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,
∴AC⊥OB,AM=CM,
∵AB=8mm,∠AOB=60°,
∴sin∠AOB=,
∴AM=(mm),
∴AC=2AM=8(mm),
故选:C.
5.C
【分析】连接OA,OC,根据垂径定理得CN=6,AM=9,设的半径为x,根据勾股定理列出方程,即可求解.
【详解】解:连接OA,OC,
∵,,
∴,
∵,,
∴CN=6,AM=9,
设的半径为x,
∵,
∴,解得:或(舍去),
经检验是方程的根,且符合题意,
∴的半径为.
故选C.
6.D
【分析】根据题意,画出这只羊在草地上的最大活动区域,然后根据扇形的面积公式计算即可.
【详解】解:如图所示:这只羊在草地上的最大活动区域为两个扇形,其中大扇形的半径为5米,圆心角为90°;小扇形的半径为5-4=1米,圆心角为180°-120°=60°
羊在草地上的最大活动区域面积==(平方米)
故选D.
7.B
【分析】连接,根据等边三角形的性质得到,根据弧长公式计算即可.
【详解】解:连接,
,
为等边三角形,
,
,
则的长,
故选.
8.D
【分析】设,利用切线长定理得到,,,然后根据勾股定理得到,最后解方程即可.
【详解】解:设,
∵直角三角形的内切圆分别与、相切于点、点,
,
,,
在中,,解得,
即的长度为.
故选D.
9.A
【分析】连接,根据菱形的性质求出和,求出长,再根据三角形的面积和扇形的面积求出即可.
【详解】解:连接,
∵四边形是菱形,
∴,
∵,为的中点,
∴,是等边三角形,,
∵,
∴,
由勾股定理得:,
∴,
∴阴影部分的面积,
故选A.
10.A
【分析】作点C关于直线AB的对称点N,DN交AB于点P1,利用直角三角形斜边中线的性质求得DM=,为定值,则点M在以D为圆心,1.5为半径的圆上,得到当点D、M、 P、N 四点在同一直线上时,DM+PM+PN有最小值,最小值为DN,利用勾股定理即可求解.
【详解】解:如图,作点C关于直线AB的对称点N,连接PN、BN、DN,
DN交AB于点P1,
∵点C、点N关于直线AB对称,
∴PC=PN,
∵△DEF是直角三角形,M是EF的中点,且EF=3,
∴DM=EF=,为定值,
∴点M在以D为圆心,1.5为半径的圆上,
∵DM+PM+PC= DM+PM+PNDN,
∴当点D、M、 P、N 四点在同一直线上时,DM+PM+PN有最小值,最小值为DN,
∴PM+PC的最小值为DN-DM=DN-,
∵正方形ABCD的边长为4,
∴CD=4,CN=8,
∴DN=,
∴PM+PC的最小值为,
故选:A.
二、填空题。
11.5
【分析】根据的面积为,可以求得的半径,再根据点在圆上,即可得到的长.
【详解】解:设的半径为,
的面积为,
,
解得,
点在圆上,
,
故答案是:5.
12.2
【分析】根据扇形面积公式S=lr计算即可.
【详解】解:∵S=lr,
∴2π=,
解得,r=2(cm),
故答案为:2.
13.70°或110°
【分析】根据圆周角定理计算即可.
【详解】解:如图,当角的顶点在优弧上时,∠ADB=∠AOB=70°;当角的顶点在劣弧上时,∠ACB=180°-∠ADB=110°;
故答案为:70°或110°.
14.
【分析】直接利用弧长公式求解即可.
【详解】解:l=,
故答案为:4π.
15.12
【分析】先计算出圆的底端距离地面的距离为12,从而得到圆的底部到弦的距离为22,从而计算出弦所对的圆心角,用弧长公式计算劣弧的长,周长减去劣弧的长得到最佳观赏路径长,除以运动速度即可.
【详解】解:如图所示,根据题意,得OC=44,CD=AD-AC=100-88=12,ED=34,
∴CE=ED-CD=34-12=22,
∴OE=OC-CE=44-22=22,
在直角三角形OEF中,sin∠OFE=,
∴∠OFE=30°,
∴∠FOE=60°,
∴∠FOB=120°,
∴,
∵圆转动的速度为,
∴最佳观赏时长为(分钟),
故答案为:12.
16.
【分析】设正六边形的中心为,连接,首先求出弓形的面积,再根据求解即可.
【详解】解:设正六边形的中心为,连接,.
由题意,,
,
.
故答案为:.
17.
【分析】由题意易得BD=4,BC=2,∠DBC=90°,∠BAE=∠BDC,然后根据三角函数可进行求解.
【详解】解:由题意得:BD=4,BC=2,∠DBC=90°,
∵∠BAE=∠BDC,
∴,
故答案为.
18.(1,4)或(6,5)
【分析】根据三角形的外心是三角形的外接圆圆心,则PA=PB=PC,故以点P为圆心,PA为半径画圆,只需点C为圆与格点的交点即可.
【详解】解:因为点P是钝角的外心,则PA=PB=PC,故以点P为圆心,PA为半径画圆,如图,
∵第一象限的点C横坐标、纵坐标均为整数,
∴点C为圆P与格点的交点,
∵△ABC为钝角三角形,
∴由图知,满足条件在点C坐标为:(1,4)或(6,5),
故答案为:(1,4)或(6,5);
三、解答题。
19.解:(1)∵AD是⊙O的直径,AD⊥BC于点E,
∴,BE=CE,
∴∠BAD=∠CAD;
(2)如图所示,连接OC,
∵∠CBG=30°,∠BEO=90°,
∴∠COG=60°,OB=2OE=6,
∴.
20.解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∴∠APC=∠ABC=60°,∠BPC=∠BAC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°﹣∠BPM=180°﹣(∠APC+∠BPC)=180°﹣120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PBC=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
在△ACM和△BCP中,
,
∴△ACM≌△BCP(AAS);
21.
(1)证明:作OF⊥AC于F,
∵⊙O与BC相切于点B,∴OB⊥BC,
∵CO平分∠ACB,
∴OF=OB ,
又OB是半径,OF⊥AC于F,
∴AC是⊙O的切线.
(2)解:∵DE是直径,
∴∠DBE=90°,
又tan∠BDE,∴,
由(1),知∵OE=OB,OB⊥BC ,
∴∠OBC=90° ,
∴∠DBC=∠OBE,
∴∠E=∠OBE,
∴∠E=∠DBC,
又 ∠C=∠C,
∴△CBE∽△CDB,
∴,
∵BC=6,
∴,
∴,
∴DE=9,
∵OD=4.5,即⊙O的半径是4.5.
22.
(1)解:连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∵的平分线交于点,交于点,
∴∠CAE=∠OAE,
∴∠CAE=∠OEA,
∵,
∴,
∵是的直径,
∴∠AEB=90°,
∴∠OEA+∠BEO=∠BEF+∠BEO=90°,即:∠OEF=∠AEB=90°,
∴OE⊥EF,
∴是的切线;
(2)由(1)可知:∠BEF=∠EAF,
又∵∠F=∠F,
∴,
∴,即:,
∴AF=40,EA=2BE,
∴AB=AF-BF=40-10=30,
∴的半径为15,
设BE=x,则AE=2x,
∴,解得:(舍去负值),
∴BE=,AE=,
∵∠CBE=∠CAE=∠EAB,
∴tan∠CBE=tan∠EAB,
∴,
∴DE=×=,
∴AD=AE-DE=-=.
23.解:(1)证:连接、
∵为的切线
∴
∵是直径,
∴,
又∵
∴
∴,
又∵
∴
∴
∴为⊙的切线;
(2)过点作于点,如下图:
由(1)得
在中,,,∴
∴(等面积法)
∴
设,则
在和中,
,
∴
解得
∴
24.解:(1)如图,连接,则,
四边形为正方形,
,
在和中,,
,
,
设,则,
在中,,
则;
(2)设,则,,
,
,
;
(3),
,
,
,解得,
,
,,
,
,
由圆周角定理得:,
,
,
,
,
在和中,,
,
,即,
解得,
如图,连接,交于点,
,,
,
四边形为正方形,
,
,
,即,
解得,
点在上运动(点与点不重合),
点在线段上运动(点与点不重合),
,即,
综上,.
25.
(1)证明:如图,连接DF,
∵是的直径,
∴.
∴DF∥AE.
∵四边形ABCD是平行四边形,
∴AE∥OC.
∴DF∥OC.
∴.
∵,
∴.
∵,
∴.
∵,
∴.
∴.
∴.
∴是的切线.
(2)解:∵,
∴.
∴.
∴.
∴.
∵,
∴.
设,则.
由勾股定理得,
即,
解得,(不合题意,舍去).
∴.
∵,
∴.
(3)解:连接MN,并延长CO与AF,分别相交于点P,点Q,连接AQ,
∵四边形ABCD是平行四边形,
∴,,AB∥OC.
∴,
∵平分,
∴.
∴.
∴.
∵
∴.
∵,
∴.
∴.
∴.
∴.
∵AB∥OC,
∴.
∴.
∵,
∴.
在Rt△APO中,由勾股定理得.
∴.
在Rt△APH中,由勾股定理得.
∵,
∴.
∵,
∴.
∴.
∴.
一、选择题:本题共10个小题,每小题3分,共30分。
1.半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,-4)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
2.一直角三角形的斜边长为c,其内切圆半径是r,则三角形面积与其内切圆的面积之比是( )
A. B. C. D.
3.如图,P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,,,则线段OP的长为( )
A.6 B.4 C.4 D.8
4.如图,要拧开一个边长为a=8mm的正六边形螺帽,扳手张开的开口b至少为( )
A.8mm B.16mm C.8mm D.4mm
5.如图,在中,弦,,,,,则的半径为( )
A.4 B. C. D.
6.如图,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊(羊在草地上活动),那么羊在草地上的最大活动区域面积是( )平方米.
A. B. C. D.
7.如图,在扇形中,为弦,,,,则的长为( )
A. B. C. D.
8.如图,直角三角形的内切圆分别与、相切于点、点,根据图中标示的长度与角度,求的长度为何?( )
A. B. C. D.
9.如图,在菱形中,点是的中点,以为圆心、为半径作弧,交于点,连接.若,,则阴影部分的面积为( )
A. B. C. D.
10.如图,正方形的边长为4,点在边上运动,点在边上运动,运动过程中的长度保持不变,且.若是的中点,是边上的动点,则的最小值为( )
A. B. C. D.
二、填空题:本题共8个小题,每题3分,共24分。
11.已知圆O的面积为,若点P在圆上,则______.
12.若一个扇形的弧长为2πcm,面积为2πcm2,则这个扇形的半径为______cm.
13.在⊙O 中,弦 AB 所对圆心角为 140°,则弦AB 所对的圆周角的度数是___________.
14.如图,为了美化校园,学校在一块靠墙角的空地上建造了一个扇形花圃,其圆心角AOB=120°,半径为6m,则扇形的弧长是_________m.(结果保留)
15.京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约.如图,摩天轮直径 88 米,最高点 A 距离地面 100 米,匀速运行一圈的时间是 18 分钟.由于受到周边建筑物的影响,乘客与地面的距离超过 34 米时,可视为最佳观赏位置,在运行的一圈里最佳观赏时长为___________分钟.
16.如图,正六边形的边长为4,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是________.
17.如图,在的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在上,点E是线段与的交点.则的正切值为________.
18.如图所示,在平面直角坐标系xOy中,点P是钝角的外心,点A、B、P的坐标分别为,,,若第一象限的点C横坐标、纵坐标均为整数,则点C的坐标为______.
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD⊥BC于点E.
(1)求证:∠BAD=∠CAD;
(2)连接BO并延长,交AC于点F,交⊙O于点G,连接GC若OE=3,∠CBG=30°,求的长.
20.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A,B重合),连接AP,BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP.
21.如图,已知,在ABC中,O为AB上一点,CO平分∠ACB,以O为圆心,OB长为半径作⊙O,⊙O与BC相切于点B,交CO于点D,延长CO交⊙O于点E,连接BD,BE.
(1)求证:AC是⊙O的切线.
(2)若tan∠BDE,BC=6,求⊙O的半径.
22.如图,已知内接干,是的直径,的平分线交于点,交于点,连接,作,交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径和的长.
23.如图,在⊙中,是直径,,垂足为P,过点的的切线与的延长线交于点, 连接.
(1)求证:为⊙的切线;
(2)若⊙半径为3,,求.
24.如图,点为以为直径的半圆的圆心,点,在直径上,点,在上,四边形为正方形,点在上运动(点与点,不重合),连接并延长交的延长线于点,连接交于点,连接.
(1)求的值;
(2)求的值;
(3)令,,直径(,是常数),求关于的函数解析式,并指明自变量的取值范围.
25.如图,已知,是的直径,,与的边,分别交于点,,连接并延长,与的延长线交于点,.
(1)求证:是的切线;
(2)若,求的值;
(3)在(2)的条件下,若的平分线交于点,连接交于点,求的值.
答案
一、选择题。
1.A
【分析】由题意先利用两点间的距离公式求出点P到原点的距离OP,再判断OP与半径r的大小关系,从而得出答案.
【详解】解:∵圆心P的坐标为(3,-4),
∴,
∵⊙P的半径为5,
∴原点O在⊙P上.
故选:A.
2.B
【分析】先画出示意图,然后连接内心和直角三角形的各个顶点,设直角三角形的两条直角边是a,b,则直角三角形的面积是,再根据正方形的判定与性质以及切线长定理可得,由此可得直角三角形的面积是,最后再结合内切圆的面积是即可求得答案.
【详解】解:如图,在中,∠C=90°,AB=c,⊙O为的内切圆,切点分别为点D、E、F,连接OA、OB、OC、OD、OE、OF,
设直角三角形的两条直角边分别为,,
∵⊙O为的内切圆,切点分别为点D、E、F,
∴
∴
,
∵
∴四边形ODCE为正方形,
∴,
∴,,
∵⊙O为的内切圆,切点分别为点D、E、F,
∴
∵,
∴,
,
∴,
又,
.
故选:B.
3.D
【分析】连接,通过直角三角形的性质求解即可.
【详解】解:连接,
∴,
∵PA为⊙O的切线,A为切点,
∴∠OAP=90°,
∵,
∴OP=2OA=8,
故选D.
4.C
【分析】由题意设正六边形的中心是O,其一边是AB,连接OA、OB、OC、AC,OB交AC于M,则∠AOB=∠BOC=60°,得出OA=OB=AB=OC=BC,则四边形ABCO是菱形,得出AC⊥OB,AM=CM,由sin∠AOB=,进而计算即可得出结果.
【详解】解:设正六边形的中心是O,其一边是AB,连接OA、OB、OC、AC,OB交AC于M,如图所示:
∴∠AOB=∠BOC=60°,OA=OB=OC
∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,
∴AC⊥OB,AM=CM,
∵AB=8mm,∠AOB=60°,
∴sin∠AOB=,
∴AM=(mm),
∴AC=2AM=8(mm),
故选:C.
5.C
【分析】连接OA,OC,根据垂径定理得CN=6,AM=9,设的半径为x,根据勾股定理列出方程,即可求解.
【详解】解:连接OA,OC,
∵,,
∴,
∵,,
∴CN=6,AM=9,
设的半径为x,
∵,
∴,解得:或(舍去),
经检验是方程的根,且符合题意,
∴的半径为.
故选C.
6.D
【分析】根据题意,画出这只羊在草地上的最大活动区域,然后根据扇形的面积公式计算即可.
【详解】解:如图所示:这只羊在草地上的最大活动区域为两个扇形,其中大扇形的半径为5米,圆心角为90°;小扇形的半径为5-4=1米,圆心角为180°-120°=60°
羊在草地上的最大活动区域面积==(平方米)
故选D.
7.B
【分析】连接,根据等边三角形的性质得到,根据弧长公式计算即可.
【详解】解:连接,
,
为等边三角形,
,
,
则的长,
故选.
8.D
【分析】设,利用切线长定理得到,,,然后根据勾股定理得到,最后解方程即可.
【详解】解:设,
∵直角三角形的内切圆分别与、相切于点、点,
,
,,
在中,,解得,
即的长度为.
故选D.
9.A
【分析】连接,根据菱形的性质求出和,求出长,再根据三角形的面积和扇形的面积求出即可.
【详解】解:连接,
∵四边形是菱形,
∴,
∵,为的中点,
∴,是等边三角形,,
∵,
∴,
由勾股定理得:,
∴,
∴阴影部分的面积,
故选A.
10.A
【分析】作点C关于直线AB的对称点N,DN交AB于点P1,利用直角三角形斜边中线的性质求得DM=,为定值,则点M在以D为圆心,1.5为半径的圆上,得到当点D、M、 P、N 四点在同一直线上时,DM+PM+PN有最小值,最小值为DN,利用勾股定理即可求解.
【详解】解:如图,作点C关于直线AB的对称点N,连接PN、BN、DN,
DN交AB于点P1,
∵点C、点N关于直线AB对称,
∴PC=PN,
∵△DEF是直角三角形,M是EF的中点,且EF=3,
∴DM=EF=,为定值,
∴点M在以D为圆心,1.5为半径的圆上,
∵DM+PM+PC= DM+PM+PNDN,
∴当点D、M、 P、N 四点在同一直线上时,DM+PM+PN有最小值,最小值为DN,
∴PM+PC的最小值为DN-DM=DN-,
∵正方形ABCD的边长为4,
∴CD=4,CN=8,
∴DN=,
∴PM+PC的最小值为,
故选:A.
二、填空题。
11.5
【分析】根据的面积为,可以求得的半径,再根据点在圆上,即可得到的长.
【详解】解:设的半径为,
的面积为,
,
解得,
点在圆上,
,
故答案是:5.
12.2
【分析】根据扇形面积公式S=lr计算即可.
【详解】解:∵S=lr,
∴2π=,
解得,r=2(cm),
故答案为:2.
13.70°或110°
【分析】根据圆周角定理计算即可.
【详解】解:如图,当角的顶点在优弧上时,∠ADB=∠AOB=70°;当角的顶点在劣弧上时,∠ACB=180°-∠ADB=110°;
故答案为:70°或110°.
14.
【分析】直接利用弧长公式求解即可.
【详解】解:l=,
故答案为:4π.
15.12
【分析】先计算出圆的底端距离地面的距离为12,从而得到圆的底部到弦的距离为22,从而计算出弦所对的圆心角,用弧长公式计算劣弧的长,周长减去劣弧的长得到最佳观赏路径长,除以运动速度即可.
【详解】解:如图所示,根据题意,得OC=44,CD=AD-AC=100-88=12,ED=34,
∴CE=ED-CD=34-12=22,
∴OE=OC-CE=44-22=22,
在直角三角形OEF中,sin∠OFE=,
∴∠OFE=30°,
∴∠FOE=60°,
∴∠FOB=120°,
∴,
∵圆转动的速度为,
∴最佳观赏时长为(分钟),
故答案为:12.
16.
【分析】设正六边形的中心为,连接,首先求出弓形的面积,再根据求解即可.
【详解】解:设正六边形的中心为,连接,.
由题意,,
,
.
故答案为:.
17.
【分析】由题意易得BD=4,BC=2,∠DBC=90°,∠BAE=∠BDC,然后根据三角函数可进行求解.
【详解】解:由题意得:BD=4,BC=2,∠DBC=90°,
∵∠BAE=∠BDC,
∴,
故答案为.
18.(1,4)或(6,5)
【分析】根据三角形的外心是三角形的外接圆圆心,则PA=PB=PC,故以点P为圆心,PA为半径画圆,只需点C为圆与格点的交点即可.
【详解】解:因为点P是钝角的外心,则PA=PB=PC,故以点P为圆心,PA为半径画圆,如图,
∵第一象限的点C横坐标、纵坐标均为整数,
∴点C为圆P与格点的交点,
∵△ABC为钝角三角形,
∴由图知,满足条件在点C坐标为:(1,4)或(6,5),
故答案为:(1,4)或(6,5);
三、解答题。
19.解:(1)∵AD是⊙O的直径,AD⊥BC于点E,
∴,BE=CE,
∴∠BAD=∠CAD;
(2)如图所示,连接OC,
∵∠CBG=30°,∠BEO=90°,
∴∠COG=60°,OB=2OE=6,
∴.
20.解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∴∠APC=∠ABC=60°,∠BPC=∠BAC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°﹣∠BPM=180°﹣(∠APC+∠BPC)=180°﹣120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PBC=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
在△ACM和△BCP中,
,
∴△ACM≌△BCP(AAS);
21.
(1)证明:作OF⊥AC于F,
∵⊙O与BC相切于点B,∴OB⊥BC,
∵CO平分∠ACB,
∴OF=OB ,
又OB是半径,OF⊥AC于F,
∴AC是⊙O的切线.
(2)解:∵DE是直径,
∴∠DBE=90°,
又tan∠BDE,∴,
由(1),知∵OE=OB,OB⊥BC ,
∴∠OBC=90° ,
∴∠DBC=∠OBE,
∴∠E=∠OBE,
∴∠E=∠DBC,
又 ∠C=∠C,
∴△CBE∽△CDB,
∴,
∵BC=6,
∴,
∴,
∴DE=9,
∵OD=4.5,即⊙O的半径是4.5.
22.
(1)解:连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∵的平分线交于点,交于点,
∴∠CAE=∠OAE,
∴∠CAE=∠OEA,
∵,
∴,
∵是的直径,
∴∠AEB=90°,
∴∠OEA+∠BEO=∠BEF+∠BEO=90°,即:∠OEF=∠AEB=90°,
∴OE⊥EF,
∴是的切线;
(2)由(1)可知:∠BEF=∠EAF,
又∵∠F=∠F,
∴,
∴,即:,
∴AF=40,EA=2BE,
∴AB=AF-BF=40-10=30,
∴的半径为15,
设BE=x,则AE=2x,
∴,解得:(舍去负值),
∴BE=,AE=,
∵∠CBE=∠CAE=∠EAB,
∴tan∠CBE=tan∠EAB,
∴,
∴DE=×=,
∴AD=AE-DE=-=.
23.解:(1)证:连接、
∵为的切线
∴
∵是直径,
∴,
又∵
∴
∴,
又∵
∴
∴
∴为⊙的切线;
(2)过点作于点,如下图:
由(1)得
在中,,,∴
∴(等面积法)
∴
设,则
在和中,
,
∴
解得
∴
24.解:(1)如图,连接,则,
四边形为正方形,
,
在和中,,
,
,
设,则,
在中,,
则;
(2)设,则,,
,
,
;
(3),
,
,
,解得,
,
,,
,
,
由圆周角定理得:,
,
,
,
,
在和中,,
,
,即,
解得,
如图,连接,交于点,
,,
,
四边形为正方形,
,
,
,即,
解得,
点在上运动(点与点不重合),
点在线段上运动(点与点不重合),
,即,
综上,.
25.
(1)证明:如图,连接DF,
∵是的直径,
∴.
∴DF∥AE.
∵四边形ABCD是平行四边形,
∴AE∥OC.
∴DF∥OC.
∴.
∵,
∴.
∵,
∴.
∵,
∴.
∴.
∴.
∴是的切线.
(2)解:∵,
∴.
∴.
∴.
∴.
∵,
∴.
设,则.
由勾股定理得,
即,
解得,(不合题意,舍去).
∴.
∵,
∴.
(3)解:连接MN,并延长CO与AF,分别相交于点P,点Q,连接AQ,
∵四边形ABCD是平行四边形,
∴,,AB∥OC.
∴,
∵平分,
∴.
∴.
∴.
∵
∴.
∵,
∴.
∴.
∴.
∴.
∵AB∥OC,
∴.
∴.
∵,
∴.
在Rt△APO中,由勾股定理得.
∴.
在Rt△APH中,由勾股定理得.
∵,
∴.
∵,
∴.
∴.
∴.
