沪教版七年级数学下册 13.1邻补角、对顶角 试题(含解析)
文档属性
| 名称 | 沪教版七年级数学下册 13.1邻补角、对顶角 试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 179.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 16:43:56 | ||
图片预览


文档简介
13.1邻补角、对顶角
一、单选题
1.下列说法中:①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.不正确的有( )
A.①② B.②③ C.②④ D.④③
2.下列说法正确的是( )
A.相等的角是对顶角; B.邻补角一定互补;
C.互补的两角一定是邻补角; D.两个角不是对顶角,则这两个角不相等;
3.下列图中,∠1和∠2是对顶角的有( )个.
A.1个 B.2个 C.3个 D.4个
4.如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
5.下列说法:
①对顶角相等;
②相等的两角一定是对顶角;
③如果两个角不是对顶角,那么它们一定不相等;
其中正确的说法有( )
A.0 B.1 C.2 D.3
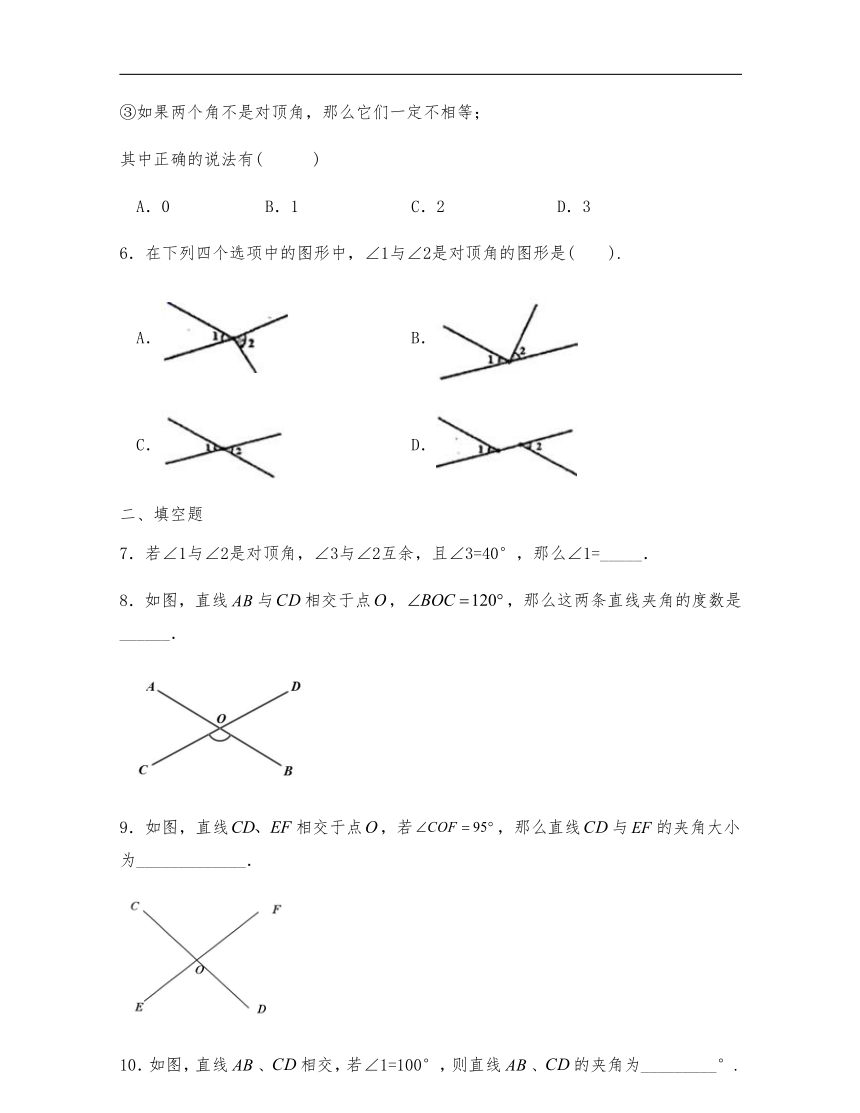
6.在下列四个选项中的图形中,∠1与∠2是对顶角的图形是( ).
A. B.
C. D.
二、填空题
7.若∠1与∠2是对顶角,∠3与∠2互余,且∠3=40°,那么∠1=_____.
8.如图,直线与相交于点,,那么这两条直线夹角的度数是______.
9.如图,直线相交于点,若,那么直线与的夹角大小为_____________.
10.如图,直线、相交,若∠1=100°,则直线、的夹角为_________°.
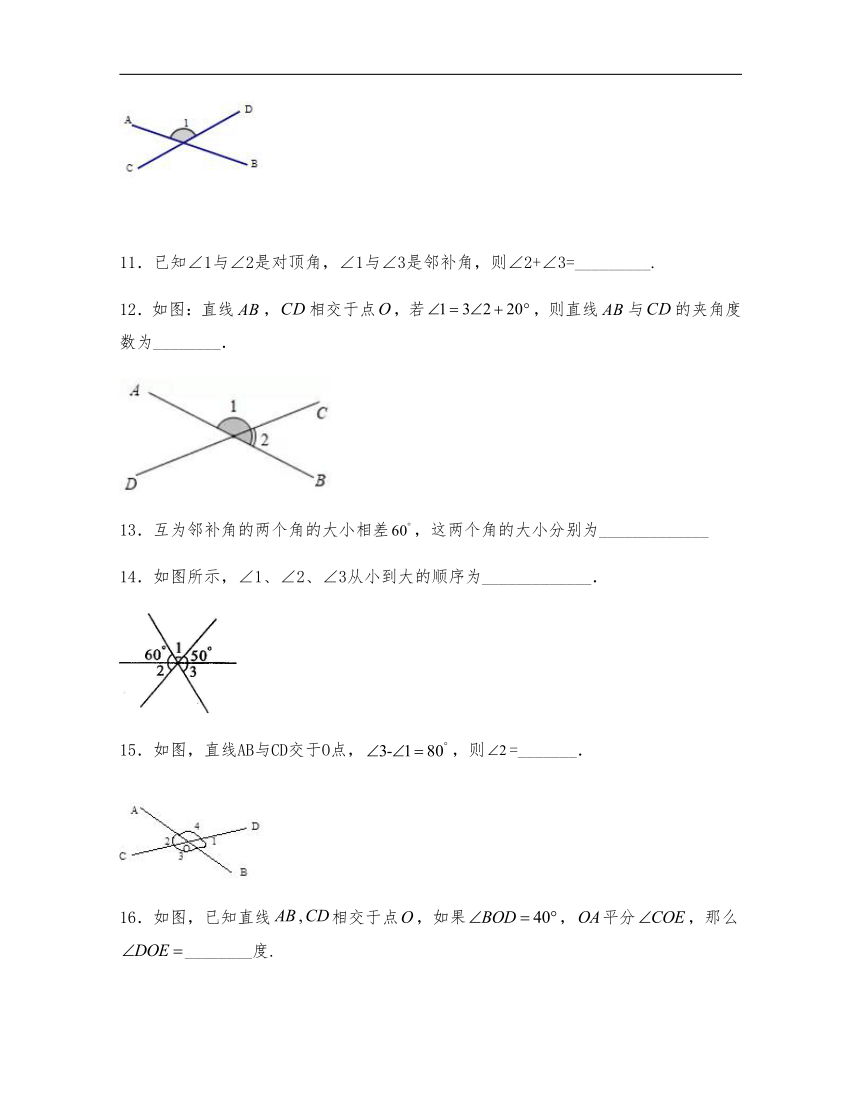
11.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3=_________.
12.如图:直线,相交于点,若,则直线与的夹角度数为________.
13.互为邻补角的两个角的大小相差,这两个角的大小分别为_____________
14.如图所示,∠1、∠2、∠3从小到大的顺序为_____________.
15.如图,直线AB与CD交于O点,,则=_______.
16.如图,已知直线相交于点,如果,平分,那么________度.
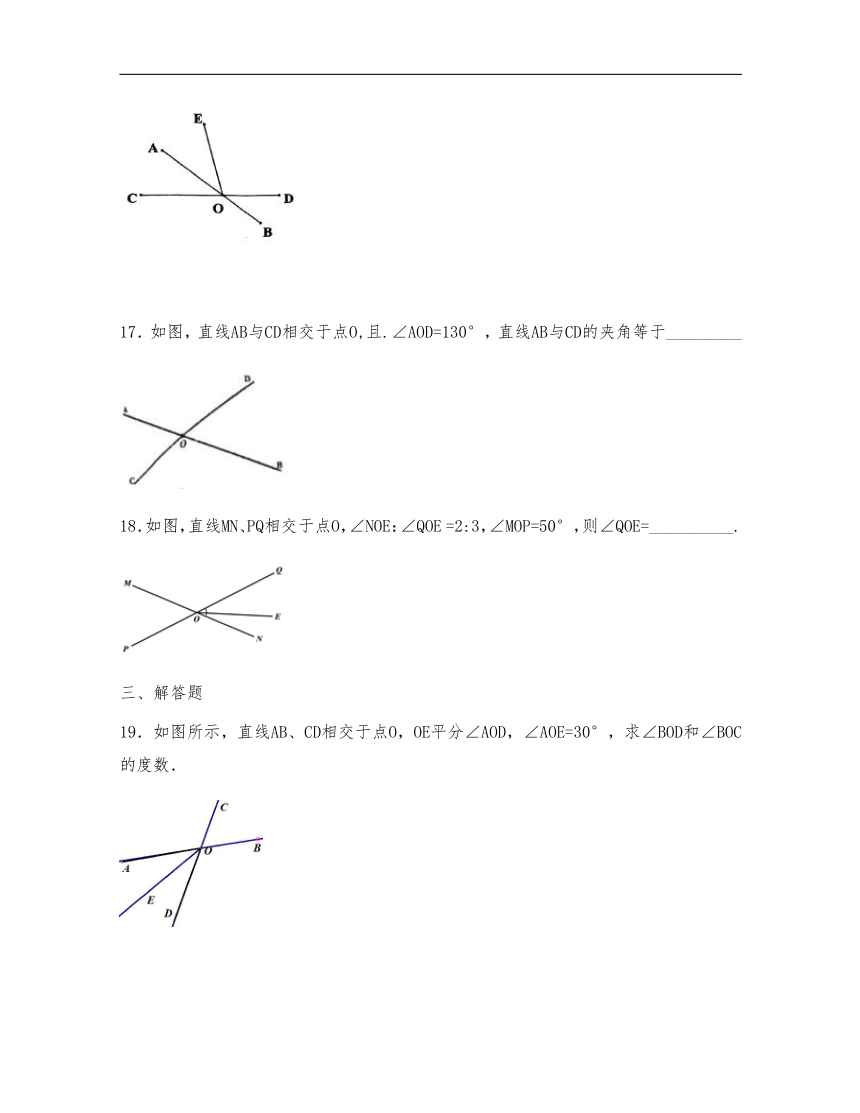
17.如图,直线AB与CD相交于点O,且.∠AOD=130°,直线AB与CD的夹角等于_________
18.如图,直线MN、PQ相交于点O,∠NOE:∠QOE =2:3,∠MOP=50°,则∠QOE=__________.
三、解答题
19.如图所示,直线AB、CD相交于点O,OE平分∠AOD,∠AOE=30°,求∠BOD和∠BOC的度数.
20.如图,已知直线a、b相交,∠1=2∠2,求∠1、∠2、∠3、∠4的度数.
21.观察图形,回答下列各题:
(1)图A中,共有____对对顶角;
(2)图B中,共有____对对顶角;
(3)图C中,共有____对对顶角;
(4)探究(1)--(3)各题中直线条数与对顶角对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;
答案
一、单选题
1.C
【分析】根据对顶角的定义和性质,逐一判断选项,即可得到答案.
【详解】∵对顶角相等,∴①不符合题意,
∵如果两个角相等,那么这两个角不一定成对顶角关系,∴②符合题意,
∵若两个角不相等,则这两个角一定不是对顶角,∴③不符合题意,
∵若两个角不是对顶角,则这两个角可能相等也可能不相等,∴④符合题意,
选C.
2.B
【分析】按照对顶角的概念和邻补角的概念逐一判断即可.
【详解】解:A项,对顶角相等,但相等的角不一定是对顶角,故本选项错误;
B项,由邻补角的定义可知,两个邻补角一定互补,故本选项正确;
C项,如30°和150°的两个角一定互补,但它们不一定是邻补角,故本选项错误;
D项,两个角不是对顶角,但它们有可能相等,如角平分线的模型,故本选项错误;
故答案为B.
3.A
【分析】根据对顶角的定义,有公共顶点且两条边都互为反向延长线的两个角称为对顶角,进行判定即可解答.
【详解】在第一幅图和第四幅图中,∠1与∠2有一条边不互为反向延长线,故不是对顶角;在第二幅图中,∠1与∠2没有公共顶点,故不是对顶角;在第三幅图中,∠1与∠2有公共顶点且两边互为反向延长线,故是对顶角.综上所述,是对顶角的图形只有1个.
故答案为A.
4.B
【解析】解:∵∠DOB=∠AOC,∴∠AOE+∠DOB+∠COF=∠AOE+∠AOC+∠COF=∠EOF=180°.故选B.
5.B
【分析】根据对顶角的定义以及性质对各选项分析判断后利用排除法求解.
【详解】解:①对顶角相等,正确;
②相等的两个角是一定对顶角,错误;
③如果两个角不是对顶角,那么它们一定不相等;错误;故选:B.
6.C
【分析】根据对顶角的定义,对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,据此即可判断.
【详解】解:根据对顶角的定义可得,四个图形中C中∠1与∠2为对顶角.故答案为:C.
二、填空题
7.50°
【分析】根据对顶角相等以及余角的定义,即可求解.
【详解】∵∠1与∠2是对顶角,∴∠1=∠2,∵∠3与∠2互余,
∴∠3+∠2=90°,∴∠3+∠1=90°,∵∠3=40°,∴∠1=50°.故答案是:50°.
8.60°
【分析】根据夹角的定义、邻补角的定义即可得.
【详解】
则这两条直线夹角的度数是
故答案为:.
9.
【分析】根据邻补角互补可得∠COE的度数,进而可得答案.
【详解】解:∵,∴,
∴直线与的夹角大小为85°,故答案为.
10.;
【分析】根据邻补角互补可得∠AOC的度数,进而可得答案.
【详解】解:∵∠1=100°,∴∠AOC=180°-100°=80°,
∴直线AB与CD的夹角是80°,故答案为:80°.
11.180°
【解析】解:∵∠1与∠3是邻补角,∴∠1+∠3=180°.∵∠1与∠2是对顶角,∴∠1=∠2,∴∠2+∠3=180°(等量代换).故答案为180°.
12.
【分析】根据是邻补角以及解出即可.
【详解】∵
又∵
∴
∴
则直线与的夹角度数为.
故答案为:
13.
【分析】设其中一个角为x,则根据邻补角的定义得另一个角为,再根据两个角的大小相差,列出方程,解方程即可
【详解】解:设其中一个角为x,则另一个角为,
∵两个角的大小相差,
∴或
∴或
∴或
故答案为:
14.∠2<∠3<∠1.
【分析】观察图形不难发现∠1+∠2+60°=180°、 ∠1+60°+50°=180°、∠1+∠3+50°=180°,求出∠1、∠2、∠3的度数,进而得出它们的大小关系.
【详解】观察图形可知:
∠1+∠2+60°=180°、 ∠1+60°+50°=180°、∠1+∠3+50°=180°
联立上述3三式解得:∠1=70° ∠2=50° ∠3=60°
故可得∠1、∠2、∠3从小到大的顺序为:∠2<∠3<∠1.
15.50°
【解析】∠3-∠1=80°, ∠3+∠1=180°,所以∠1=50°, 则∠2=50°.
16.100
【分析】根据对顶角相等求出∠AOC,再根据角平分线和邻补角的定义解答.
【详解】解:∵∠BOD=40°,∴∠AOC=∠BOD=40°,
∵OA平分∠COE,∴∠AOE=∠AOC=40°,∴∠COE=80°.
∴∠DOE=180°-80°=100°故答案为100.
17.50°
【分析】根据邻补角可得∠AOC的度数,即可解答.
【详解】解:∵∠AOD=130°,∴∠AOC=180°-130°=50°,∴直线AB与CD的夹角是50°,故答案为50°.
18.30°
【分析】根据对顶角相等,可知∠MOP=∠QON=50°,然后根据∠NOE:∠QOE =2:3即可求得答案.
【详解】根据对顶角相等,可知∠MOP=∠QON=50°,又∠NOE:∠QOE =2:3,
所以∠QOE=30°.故答案为30°.
三、解答题
19.∵OE平分∠AOD,∴∠AOD=2∠AOE;
∵∠AOE=30°,∴∠AOD=60°,
∵∠AOD和∠BOC是对顶角,∴∠BOC=60°,
∵∠AOD和∠BOD是互补,∴∠BOD=120°.
20.∵∠1和∠2互补,∠1=2∠2,∴∠1=120°,∠2=60°,
∵∠1和∠3,∠2和∠4是对顶角,∴∠3=120°,∠4=60°.
21.
(1)2对;
(2)6对;
(3)12对;
(4)2条直线相交时,对顶角对数为:1×2=2对;
3条直线相交时,对顶角对数为:3×2=6对;
4条直线相交时,对顶角对数为:4×3=12对;
…
n条直线相交时,对顶角对数为:n(n-1)(n≥2)对.
一、单选题
1.下列说法中:①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.不正确的有( )
A.①② B.②③ C.②④ D.④③
2.下列说法正确的是( )
A.相等的角是对顶角; B.邻补角一定互补;
C.互补的两角一定是邻补角; D.两个角不是对顶角,则这两个角不相等;
3.下列图中,∠1和∠2是对顶角的有( )个.
A.1个 B.2个 C.3个 D.4个
4.如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
5.下列说法:
①对顶角相等;
②相等的两角一定是对顶角;
③如果两个角不是对顶角,那么它们一定不相等;
其中正确的说法有( )
A.0 B.1 C.2 D.3
6.在下列四个选项中的图形中,∠1与∠2是对顶角的图形是( ).
A. B.
C. D.
二、填空题
7.若∠1与∠2是对顶角,∠3与∠2互余,且∠3=40°,那么∠1=_____.
8.如图,直线与相交于点,,那么这两条直线夹角的度数是______.
9.如图,直线相交于点,若,那么直线与的夹角大小为_____________.
10.如图,直线、相交,若∠1=100°,则直线、的夹角为_________°.
11.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3=_________.
12.如图:直线,相交于点,若,则直线与的夹角度数为________.
13.互为邻补角的两个角的大小相差,这两个角的大小分别为_____________
14.如图所示,∠1、∠2、∠3从小到大的顺序为_____________.
15.如图,直线AB与CD交于O点,,则=_______.
16.如图,已知直线相交于点,如果,平分,那么________度.
17.如图,直线AB与CD相交于点O,且.∠AOD=130°,直线AB与CD的夹角等于_________
18.如图,直线MN、PQ相交于点O,∠NOE:∠QOE =2:3,∠MOP=50°,则∠QOE=__________.
三、解答题
19.如图所示,直线AB、CD相交于点O,OE平分∠AOD,∠AOE=30°,求∠BOD和∠BOC的度数.
20.如图,已知直线a、b相交,∠1=2∠2,求∠1、∠2、∠3、∠4的度数.
21.观察图形,回答下列各题:
(1)图A中,共有____对对顶角;
(2)图B中,共有____对对顶角;
(3)图C中,共有____对对顶角;
(4)探究(1)--(3)各题中直线条数与对顶角对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;
答案
一、单选题
1.C
【分析】根据对顶角的定义和性质,逐一判断选项,即可得到答案.
【详解】∵对顶角相等,∴①不符合题意,
∵如果两个角相等,那么这两个角不一定成对顶角关系,∴②符合题意,
∵若两个角不相等,则这两个角一定不是对顶角,∴③不符合题意,
∵若两个角不是对顶角,则这两个角可能相等也可能不相等,∴④符合题意,
选C.
2.B
【分析】按照对顶角的概念和邻补角的概念逐一判断即可.
【详解】解:A项,对顶角相等,但相等的角不一定是对顶角,故本选项错误;
B项,由邻补角的定义可知,两个邻补角一定互补,故本选项正确;
C项,如30°和150°的两个角一定互补,但它们不一定是邻补角,故本选项错误;
D项,两个角不是对顶角,但它们有可能相等,如角平分线的模型,故本选项错误;
故答案为B.
3.A
【分析】根据对顶角的定义,有公共顶点且两条边都互为反向延长线的两个角称为对顶角,进行判定即可解答.
【详解】在第一幅图和第四幅图中,∠1与∠2有一条边不互为反向延长线,故不是对顶角;在第二幅图中,∠1与∠2没有公共顶点,故不是对顶角;在第三幅图中,∠1与∠2有公共顶点且两边互为反向延长线,故是对顶角.综上所述,是对顶角的图形只有1个.
故答案为A.
4.B
【解析】解:∵∠DOB=∠AOC,∴∠AOE+∠DOB+∠COF=∠AOE+∠AOC+∠COF=∠EOF=180°.故选B.
5.B
【分析】根据对顶角的定义以及性质对各选项分析判断后利用排除法求解.
【详解】解:①对顶角相等,正确;
②相等的两个角是一定对顶角,错误;
③如果两个角不是对顶角,那么它们一定不相等;错误;故选:B.
6.C
【分析】根据对顶角的定义,对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,据此即可判断.
【详解】解:根据对顶角的定义可得,四个图形中C中∠1与∠2为对顶角.故答案为:C.
二、填空题
7.50°
【分析】根据对顶角相等以及余角的定义,即可求解.
【详解】∵∠1与∠2是对顶角,∴∠1=∠2,∵∠3与∠2互余,
∴∠3+∠2=90°,∴∠3+∠1=90°,∵∠3=40°,∴∠1=50°.故答案是:50°.
8.60°
【分析】根据夹角的定义、邻补角的定义即可得.
【详解】
则这两条直线夹角的度数是
故答案为:.
9.
【分析】根据邻补角互补可得∠COE的度数,进而可得答案.
【详解】解:∵,∴,
∴直线与的夹角大小为85°,故答案为.
10.;
【分析】根据邻补角互补可得∠AOC的度数,进而可得答案.
【详解】解:∵∠1=100°,∴∠AOC=180°-100°=80°,
∴直线AB与CD的夹角是80°,故答案为:80°.
11.180°
【解析】解:∵∠1与∠3是邻补角,∴∠1+∠3=180°.∵∠1与∠2是对顶角,∴∠1=∠2,∴∠2+∠3=180°(等量代换).故答案为180°.
12.
【分析】根据是邻补角以及解出即可.
【详解】∵
又∵
∴
∴
则直线与的夹角度数为.
故答案为:
13.
【分析】设其中一个角为x,则根据邻补角的定义得另一个角为,再根据两个角的大小相差,列出方程,解方程即可
【详解】解:设其中一个角为x,则另一个角为,
∵两个角的大小相差,
∴或
∴或
∴或
故答案为:
14.∠2<∠3<∠1.
【分析】观察图形不难发现∠1+∠2+60°=180°、 ∠1+60°+50°=180°、∠1+∠3+50°=180°,求出∠1、∠2、∠3的度数,进而得出它们的大小关系.
【详解】观察图形可知:
∠1+∠2+60°=180°、 ∠1+60°+50°=180°、∠1+∠3+50°=180°
联立上述3三式解得:∠1=70° ∠2=50° ∠3=60°
故可得∠1、∠2、∠3从小到大的顺序为:∠2<∠3<∠1.
15.50°
【解析】∠3-∠1=80°, ∠3+∠1=180°,所以∠1=50°, 则∠2=50°.
16.100
【分析】根据对顶角相等求出∠AOC,再根据角平分线和邻补角的定义解答.
【详解】解:∵∠BOD=40°,∴∠AOC=∠BOD=40°,
∵OA平分∠COE,∴∠AOE=∠AOC=40°,∴∠COE=80°.
∴∠DOE=180°-80°=100°故答案为100.
17.50°
【分析】根据邻补角可得∠AOC的度数,即可解答.
【详解】解:∵∠AOD=130°,∴∠AOC=180°-130°=50°,∴直线AB与CD的夹角是50°,故答案为50°.
18.30°
【分析】根据对顶角相等,可知∠MOP=∠QON=50°,然后根据∠NOE:∠QOE =2:3即可求得答案.
【详解】根据对顶角相等,可知∠MOP=∠QON=50°,又∠NOE:∠QOE =2:3,
所以∠QOE=30°.故答案为30°.
三、解答题
19.∵OE平分∠AOD,∴∠AOD=2∠AOE;
∵∠AOE=30°,∴∠AOD=60°,
∵∠AOD和∠BOC是对顶角,∴∠BOC=60°,
∵∠AOD和∠BOD是互补,∴∠BOD=120°.
20.∵∠1和∠2互补,∠1=2∠2,∴∠1=120°,∠2=60°,
∵∠1和∠3,∠2和∠4是对顶角,∴∠3=120°,∠4=60°.
21.
(1)2对;
(2)6对;
(3)12对;
(4)2条直线相交时,对顶角对数为:1×2=2对;
3条直线相交时,对顶角对数为:3×2=6对;
4条直线相交时,对顶角对数为:4×3=12对;
…
n条直线相交时,对顶角对数为:n(n-1)(n≥2)对.
