沪教版七年级数学下册 13.5 平行线的性质 同步练习 (含解析)
文档属性
| 名称 | 沪教版七年级数学下册 13.5 平行线的性质 同步练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 372.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 16:46:48 | ||
图片预览




文档简介
13.5 平行线的性质
一、单选题
1.若∠1和∠2是同旁内角,若∠1=45°,则∠2的度数是 ( )
A.45° B.135° C.45°或135° D.不能确定
2.如图,直线,点在直线上,且,,则的度数为( )
A. B. C. D.
3.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
4.已知两条直线被第三条直线所截,下列四个说法中正确的个数是( )
(1)同位角的角平分线互相平行;(2)内错角的角平分线互相平行;(3)同旁内角的角平分线互相垂直;(4)邻补角的角平分线互相垂直
A.4个 B.3个 C.2个 D.1个
5.如图,已知,那么使成立的另一个条件是( )
A. B. C. D.
6.如果两个角的两边分别平行,其中一个角是50°,则另一个角是( )
A.50° B.130° C.50°或130° D.40°
7.已知同一平面上的两个角的两条边分别平行,则这两个角( )
A.相等 B.相等或互补 C.互补 D.互余
8.把一张对面互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论不正确的有( ).
A. B.∠AEC=148° C.∠BGE=64° D.∠BFD=116°
9.如图,AE∥BF,∠1=110°,∠2=130°,那么∠3的度数是( )
A.40° B.50° C.60° D.70°
10.如图,a∥b,点B在直线b上,且AB⊥BC,∠1=36°,那么∠2=( )
A.54° B.56° C.44° D.46°
二、填空题
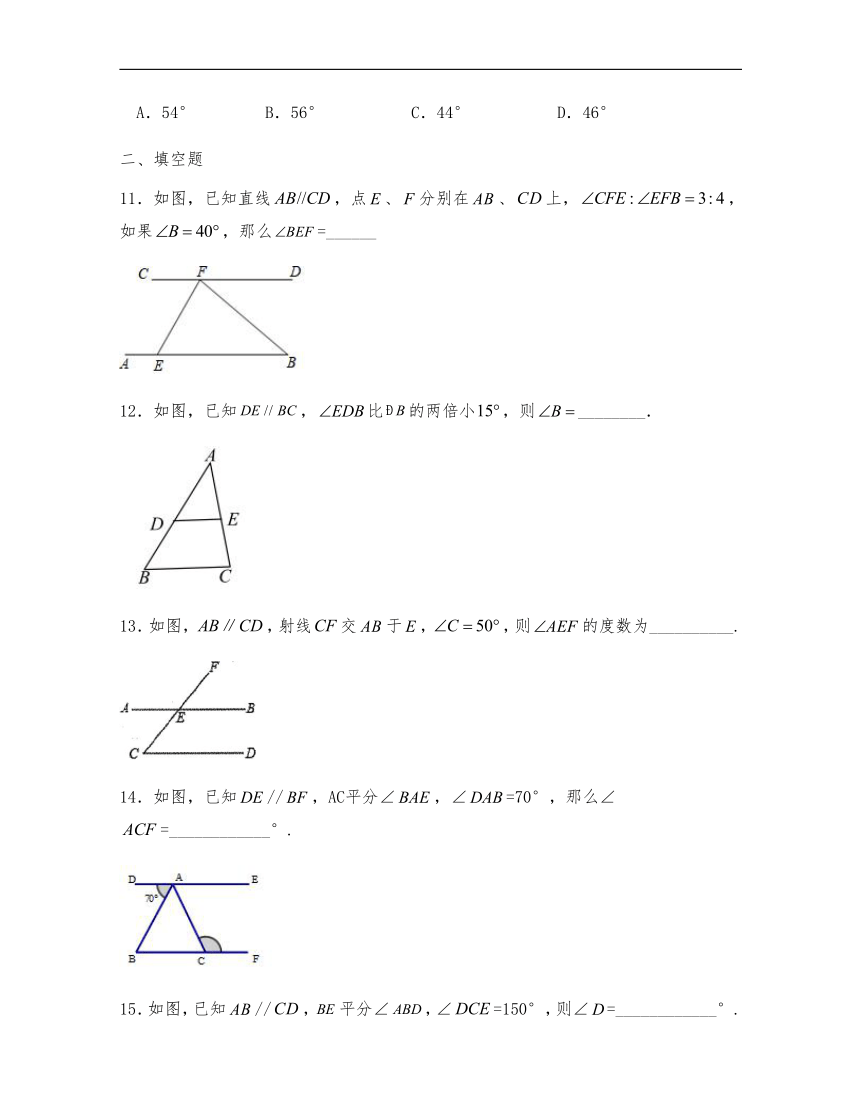
11.如图,已知直线,点、分别在、上,,如果,那么=______
12.如图,已知,比的两倍小,则________.
13.如图,,射线交于,,则的度数为__________.
14.如图,已知//,AC平分∠,∠=70°,那么∠=____________°.
15.如图,已知//,平分∠,∠=150°,则∠=____________°.
16.如图,一个合格的弯形管道,经两次拐弯后保持平行(即.如果,那么的度数是__________ 度
三、解答题
17.如图,已知AB∥DE,那么∠A+∠C+∠D的和是多少度?为什么?
18.如图,点在上,已知,,请说明的理由.
19.如图,已知,垂足为点,,垂足为点 ,. 请填写的理由.
,
,( )
( )
( )
( )
.
20.看图填空,把解题过程补全.
如图,已知,垂足为,,垂足为,∠1+∠2=180°,请填写的理由.
解:因为,(已知)
所以,( ),
得( )
所以( ),
得∠2+∠3=180°( )
由∠1+∠2=180°( ),
得∠1=∠3( ),
所以( ),
得( ).
21.已知:∠BAP+∠APD=180°,∠E=∠F,请问:∠1、∠2相等吗?,阐述理由.
22.已知:如图,,,那么吗?请说明理由.
23.如图,、、三点在同一条直线上,,,说明.
解:因为(已知),
所以(_______________________),
所以___________(____________________________),
因为(已知)
所以_______________________,
所以AC∥ED(_______________________).
答案
一、单选题
1.D
【分析】根据如果两直线平行时同旁内角互补,不平行时无法确定同旁内角的大小关系进行解答.
【详解】解:∵没有说明两直线是否平行,
∴无法判断∠1与∠2的大小关系,故选:D.
2.A
【解析】
∵a∥b,
∴∠1=∠3.
∵∠1=55°,
∴∠3=55°.
∵AB⊥BC,
∴∠ABC=90°,
∴∠2+∠3=90°,
∴∠2=35°.
故选A.
3.C
试题分析:根据平行线的判定进行判断即可.
解:A、若a∥b,b∥c,则a∥c,利用了平行公理,正确;
B、若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;
C、∠3=∠2,不能判断b∥c,错误;
D、若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;
故选C.
4.D
【分析】根据平行线的判定定理解答.
【详解】(1)两条平行直线被第三条直线所截,同位角的角平分线互相平行,故错误.
(2)两条平行直线被第三条直线所截,内错角的角平分线互相平行,故错误.
(3)两条平行直线被第三条直线所截,同旁内角的角平分线互相垂直,故错误.
(4)邻补角的角平分线互相垂直,故本选项正确.
综上所述,正确的说法只有1个.
故选:D.
5.D
【分析】对各个选项的条件进行分析,根据平行线的判定与性质即可求得正确选项.
【详解】解:A、由,无法证明,故本选项不符合题意;
B、由,无法证明,故本选项不符合题意;
C、由,无法证明,故本选项不符合题意;
D、由得,
∴,
又∵,
∴,
∴,
故本选项符合题意;
故选:D.
6.C
【分析】根据题意作图,可得:∠2与∠3的两边都与∠1的两边分别平行,然后根据两直线平行,同旁内角互补,即可求得∠3的度数,又由邻补角的定义,即可求得∠2的度数,即可求得答案.
【详解】解:如图:
∠2与∠3的都两边与∠1的两边分别平行,
即AB∥CD,AD∥BC,
∴∠1+∠A=180°,∠3+∠A=180°,
∴∠3=∠1=50°,
∵∠2+∠3=180°,
∴∠2=130°.
故另一个角是50°或130°.故选:C.
7.B
【分析】首先根据题意作图,然后由平行线的性质与邻补角的定义,即可求得同一平面上的两个角的两条边分别平行,则这两个角相等或互补.
【详解】解:如图:
∵AD∥BC,AB∥CD,
∴∠B+∠BAD=180°,∠ADC+∠BAD=180°,
∴∠B=∠ADC,
∵∠ADC+∠CDE=180°,
∴∠B+∠CDE=180°.
∴同一平面上的两个角的两条边分别平行,则这两个角相等或互补.
故选:B.
8.B
【分析】根据平行线的性质及翻折变换的性质对各选项进行逐一分析即可.
【详解】A.∵AE∥BG,∠EFB=32°,
∴∠C′EF=∠EFB=32°,故正确;
B.∵AE∥BG,∠EFB=32°,
∴∠AEF=180°-∠EFB=180°-32°=148°,
∵∠AEF=∠AEC+∠GEF,
∴∠AEC<148°,故错误;
C.∵∠C′EF=32°,
∴∠GEF=∠C′EF=32°,
∴∠C′EG=∠C′EF+∠GEF=32°+32°=64°,
∵AC′∥BD′,
∴∠BGE=∠C′EG=64°,故正确;
D.∵∠BGE=64°,
∴∠CGF=∠BGE=64°,
∵DF∥CG,
∴∠BFD=180°-∠CGF=180°-64°=116°,故正确.
故选B.
9.C
【分析】延长AC交FB的延长线于点D,根据平行线性质定理即可解答.
【详解】解:如图,延长AC交FB的延长线于点D,∵AE∥BF,
∴∠4=180°﹣∠1=70°,∴∠3=∠2﹣∠4=60°.故选:C.
10.A
【分析】先根据AB⊥BC,即可得到 .再根据 ,即可得出.
【详解】由题意可知:如下图所示
∵AB⊥BC,∠1=36°,
∴
∵,
∴
故选A.
二、填空题
11.
【分析】由平行线可得∠DFB=∠B,∠BEF=∠CFE,然后求出∠BFC,再根据比例关系求出∠CFE,即可得出结果.
【详解】∵AB∥CD
∴∠DFB=∠B=40°,∠BEF=∠CFE
∴∠BFC=
∵
∴
∴∠BEF=∠CFE=
故答案为:
12.
【分析】先根据平行线性质得出,再根据即可求出答案.
【详解】
故答案为:
13.
【分析】先根据平行线的性质求出∠FEB=∠C=50°,继而再根据邻补角定义进行求解即可.
【详解】∵AB//CD,
∴∠FEB=∠C=50°,
∴∠AEF=180°-∠FEB=180°-50°=130°,
故答案为130°.
14.125°;
【分析】根据已知及补角的性质可求得∠EAB的度数,再根据角平分线的性质可求得∠EAC的度数,再根据平行线的性质可求得∠ACF的度数.
【详解】解:∵∠=70°,
∴∠EAB =180°-70°=110°,
∵AC平分∠BAE,
∴∠CAE=55°,
∵DE∥BF,
∴∠ACF=180°-∠EAC=125°.
故答案是:125°.
15.120;
【分析】根据邻补角的定义求出∠DCB,再根据两直线平行,内错角相等求出∠ABE,然后根据角平分线的定义求出∠ABD,再根据两直线平行,同旁内角互补解答即可.
【详解】解:∵∠=150°,,
∴∠DCB =180°-∠ =180°-150°=30°,
∵AB∥CD,
∴∠ABE=∠DCB =30°,
∵BE平分∠ABC,
∴∠ABD=2∠ABE=2×30°=60°,
∵AB∥CD,
∴∠D=180°-∠ABD=180°-60°=120°.
故答案为:120.
16.∠B=120°
分析:利用两直线平行,同旁内角互补求解.
详解:∵AB∥DC,
∴
故答案为.
三、解答题
17.
如图,过点C作,则所求的问题变为的和是多少度
即.
18.解:∵, ,
∴,又∵,
∴,∴,∴.
19.解:∠CGD=∠CAB,理由如下:
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠3+∠2=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°,
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB.
故答案为:垂直定义;EF;同位角相等,两直线平行;3;两直线平行,同旁内角互补;1;3;同角的补角相等;AB;内错角相等,两直线平行.
20.解:因为,(已知)
所以,(垂直的定义),
得(等量代换)
所以(同位角相等,两直线平行),
得∠2+∠3=180°(两直线平行,同旁内角互补)
由∠1+∠2=180°(已知),
得∠1=∠3(同角的补角相等),
所以(内错角相等,两直线平行),
得(两直线平行,同位角相等).
21.证明:∵∠BAP+∠APD=180°(已知),
∴AB∥CD,
∴∠BAP=∠APC,
又∵∠E=∠F,
∴AE∥PF
∴∠FPA=∠EAP,
∴∠BAP-∠EAP=∠APC-∠FPA
∴∠1=∠2.
22.解:相等,理由如下:
因为
所以(内错角相等,两直线平等)
所以(两直线平行,内错角相等)
又因为,
所以(两直线平行,同位角相等).
所以(等量代换).
23.解:因为(已知),
所以(同旁内角互补,两直线平行),
所以 (两直线平行,内错角相等),
因为(已知)
所以,
所以AC∥ED(内错角相等,两直线平行).
一、单选题
1.若∠1和∠2是同旁内角,若∠1=45°,则∠2的度数是 ( )
A.45° B.135° C.45°或135° D.不能确定
2.如图,直线,点在直线上,且,,则的度数为( )
A. B. C. D.
3.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
4.已知两条直线被第三条直线所截,下列四个说法中正确的个数是( )
(1)同位角的角平分线互相平行;(2)内错角的角平分线互相平行;(3)同旁内角的角平分线互相垂直;(4)邻补角的角平分线互相垂直
A.4个 B.3个 C.2个 D.1个
5.如图,已知,那么使成立的另一个条件是( )
A. B. C. D.
6.如果两个角的两边分别平行,其中一个角是50°,则另一个角是( )
A.50° B.130° C.50°或130° D.40°
7.已知同一平面上的两个角的两条边分别平行,则这两个角( )
A.相等 B.相等或互补 C.互补 D.互余
8.把一张对面互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论不正确的有( ).
A. B.∠AEC=148° C.∠BGE=64° D.∠BFD=116°
9.如图,AE∥BF,∠1=110°,∠2=130°,那么∠3的度数是( )
A.40° B.50° C.60° D.70°
10.如图,a∥b,点B在直线b上,且AB⊥BC,∠1=36°,那么∠2=( )
A.54° B.56° C.44° D.46°
二、填空题
11.如图,已知直线,点、分别在、上,,如果,那么=______
12.如图,已知,比的两倍小,则________.
13.如图,,射线交于,,则的度数为__________.
14.如图,已知//,AC平分∠,∠=70°,那么∠=____________°.
15.如图,已知//,平分∠,∠=150°,则∠=____________°.
16.如图,一个合格的弯形管道,经两次拐弯后保持平行(即.如果,那么的度数是__________ 度
三、解答题
17.如图,已知AB∥DE,那么∠A+∠C+∠D的和是多少度?为什么?
18.如图,点在上,已知,,请说明的理由.
19.如图,已知,垂足为点,,垂足为点 ,. 请填写的理由.
,
,( )
( )
( )
( )
.
20.看图填空,把解题过程补全.
如图,已知,垂足为,,垂足为,∠1+∠2=180°,请填写的理由.
解:因为,(已知)
所以,( ),
得( )
所以( ),
得∠2+∠3=180°( )
由∠1+∠2=180°( ),
得∠1=∠3( ),
所以( ),
得( ).
21.已知:∠BAP+∠APD=180°,∠E=∠F,请问:∠1、∠2相等吗?,阐述理由.
22.已知:如图,,,那么吗?请说明理由.
23.如图,、、三点在同一条直线上,,,说明.
解:因为(已知),
所以(_______________________),
所以___________(____________________________),
因为(已知)
所以_______________________,
所以AC∥ED(_______________________).
答案
一、单选题
1.D
【分析】根据如果两直线平行时同旁内角互补,不平行时无法确定同旁内角的大小关系进行解答.
【详解】解:∵没有说明两直线是否平行,
∴无法判断∠1与∠2的大小关系,故选:D.
2.A
【解析】
∵a∥b,
∴∠1=∠3.
∵∠1=55°,
∴∠3=55°.
∵AB⊥BC,
∴∠ABC=90°,
∴∠2+∠3=90°,
∴∠2=35°.
故选A.
3.C
试题分析:根据平行线的判定进行判断即可.
解:A、若a∥b,b∥c,则a∥c,利用了平行公理,正确;
B、若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;
C、∠3=∠2,不能判断b∥c,错误;
D、若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;
故选C.
4.D
【分析】根据平行线的判定定理解答.
【详解】(1)两条平行直线被第三条直线所截,同位角的角平分线互相平行,故错误.
(2)两条平行直线被第三条直线所截,内错角的角平分线互相平行,故错误.
(3)两条平行直线被第三条直线所截,同旁内角的角平分线互相垂直,故错误.
(4)邻补角的角平分线互相垂直,故本选项正确.
综上所述,正确的说法只有1个.
故选:D.
5.D
【分析】对各个选项的条件进行分析,根据平行线的判定与性质即可求得正确选项.
【详解】解:A、由,无法证明,故本选项不符合题意;
B、由,无法证明,故本选项不符合题意;
C、由,无法证明,故本选项不符合题意;
D、由得,
∴,
又∵,
∴,
∴,
故本选项符合题意;
故选:D.
6.C
【分析】根据题意作图,可得:∠2与∠3的两边都与∠1的两边分别平行,然后根据两直线平行,同旁内角互补,即可求得∠3的度数,又由邻补角的定义,即可求得∠2的度数,即可求得答案.
【详解】解:如图:
∠2与∠3的都两边与∠1的两边分别平行,
即AB∥CD,AD∥BC,
∴∠1+∠A=180°,∠3+∠A=180°,
∴∠3=∠1=50°,
∵∠2+∠3=180°,
∴∠2=130°.
故另一个角是50°或130°.故选:C.
7.B
【分析】首先根据题意作图,然后由平行线的性质与邻补角的定义,即可求得同一平面上的两个角的两条边分别平行,则这两个角相等或互补.
【详解】解:如图:
∵AD∥BC,AB∥CD,
∴∠B+∠BAD=180°,∠ADC+∠BAD=180°,
∴∠B=∠ADC,
∵∠ADC+∠CDE=180°,
∴∠B+∠CDE=180°.
∴同一平面上的两个角的两条边分别平行,则这两个角相等或互补.
故选:B.
8.B
【分析】根据平行线的性质及翻折变换的性质对各选项进行逐一分析即可.
【详解】A.∵AE∥BG,∠EFB=32°,
∴∠C′EF=∠EFB=32°,故正确;
B.∵AE∥BG,∠EFB=32°,
∴∠AEF=180°-∠EFB=180°-32°=148°,
∵∠AEF=∠AEC+∠GEF,
∴∠AEC<148°,故错误;
C.∵∠C′EF=32°,
∴∠GEF=∠C′EF=32°,
∴∠C′EG=∠C′EF+∠GEF=32°+32°=64°,
∵AC′∥BD′,
∴∠BGE=∠C′EG=64°,故正确;
D.∵∠BGE=64°,
∴∠CGF=∠BGE=64°,
∵DF∥CG,
∴∠BFD=180°-∠CGF=180°-64°=116°,故正确.
故选B.
9.C
【分析】延长AC交FB的延长线于点D,根据平行线性质定理即可解答.
【详解】解:如图,延长AC交FB的延长线于点D,∵AE∥BF,
∴∠4=180°﹣∠1=70°,∴∠3=∠2﹣∠4=60°.故选:C.
10.A
【分析】先根据AB⊥BC,即可得到 .再根据 ,即可得出.
【详解】由题意可知:如下图所示
∵AB⊥BC,∠1=36°,
∴
∵,
∴
故选A.
二、填空题
11.
【分析】由平行线可得∠DFB=∠B,∠BEF=∠CFE,然后求出∠BFC,再根据比例关系求出∠CFE,即可得出结果.
【详解】∵AB∥CD
∴∠DFB=∠B=40°,∠BEF=∠CFE
∴∠BFC=
∵
∴
∴∠BEF=∠CFE=
故答案为:
12.
【分析】先根据平行线性质得出,再根据即可求出答案.
【详解】
故答案为:
13.
【分析】先根据平行线的性质求出∠FEB=∠C=50°,继而再根据邻补角定义进行求解即可.
【详解】∵AB//CD,
∴∠FEB=∠C=50°,
∴∠AEF=180°-∠FEB=180°-50°=130°,
故答案为130°.
14.125°;
【分析】根据已知及补角的性质可求得∠EAB的度数,再根据角平分线的性质可求得∠EAC的度数,再根据平行线的性质可求得∠ACF的度数.
【详解】解:∵∠=70°,
∴∠EAB =180°-70°=110°,
∵AC平分∠BAE,
∴∠CAE=55°,
∵DE∥BF,
∴∠ACF=180°-∠EAC=125°.
故答案是:125°.
15.120;
【分析】根据邻补角的定义求出∠DCB,再根据两直线平行,内错角相等求出∠ABE,然后根据角平分线的定义求出∠ABD,再根据两直线平行,同旁内角互补解答即可.
【详解】解:∵∠=150°,,
∴∠DCB =180°-∠ =180°-150°=30°,
∵AB∥CD,
∴∠ABE=∠DCB =30°,
∵BE平分∠ABC,
∴∠ABD=2∠ABE=2×30°=60°,
∵AB∥CD,
∴∠D=180°-∠ABD=180°-60°=120°.
故答案为:120.
16.∠B=120°
分析:利用两直线平行,同旁内角互补求解.
详解:∵AB∥DC,
∴
故答案为.
三、解答题
17.
如图,过点C作,则所求的问题变为的和是多少度
即.
18.解:∵, ,
∴,又∵,
∴,∴,∴.
19.解:∠CGD=∠CAB,理由如下:
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠3+∠2=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°,
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB.
故答案为:垂直定义;EF;同位角相等,两直线平行;3;两直线平行,同旁内角互补;1;3;同角的补角相等;AB;内错角相等,两直线平行.
20.解:因为,(已知)
所以,(垂直的定义),
得(等量代换)
所以(同位角相等,两直线平行),
得∠2+∠3=180°(两直线平行,同旁内角互补)
由∠1+∠2=180°(已知),
得∠1=∠3(同角的补角相等),
所以(内错角相等,两直线平行),
得(两直线平行,同位角相等).
21.证明:∵∠BAP+∠APD=180°(已知),
∴AB∥CD,
∴∠BAP=∠APC,
又∵∠E=∠F,
∴AE∥PF
∴∠FPA=∠EAP,
∴∠BAP-∠EAP=∠APC-∠FPA
∴∠1=∠2.
22.解:相等,理由如下:
因为
所以(内错角相等,两直线平等)
所以(两直线平行,内错角相等)
又因为,
所以(两直线平行,同位角相等).
所以(等量代换).
23.解:因为(已知),
所以(同旁内角互补,两直线平行),
所以 (两直线平行,内错角相等),
因为(已知)
所以,
所以AC∥ED(内错角相等,两直线平行).
