八年级数学下册试题 第22章《四边形》章节复习题-沪教版(含答案)
文档属性
| 名称 | 八年级数学下册试题 第22章《四边形》章节复习题-沪教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览



文档简介
第22章《四边形》章节复习题
一.选择题
1.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
2.正多边形的一个内角为144°,那么该正多边形的边数为( )
A.8 B.9 C.10 D.11
3.已知非零向量,,,下列条件中,不能判定向量与向量平行的是( )
A.∥,∥ B.||=2|| C.=2,=3 D.+2=
4.如果一个多边形的内角和等于900°,那么这个多边形的边数是( )
A.6 B.7 C.8 D.9
5.下列四个命题中,真命题是( )
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.以一条对角线为对称轴的四边形是菱形
D.对称轴互相垂直的四边形是矩形
6.如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是( )
A.180° B.270° C.360° D.540°
7.已知、是两个单位向量,向量=3,=﹣3,那么下列结论正确的是( )
A.= B.=﹣ C.||=|| D.||=﹣||
8.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
二.填空题
9.如图,已知平行四边形ABCD的对角线AC与BD交于点O.设=,=,那么向量关于向量、的分解式是 .
10.从七边形的一个顶点出发可以画出 条对角线.
11.如果一个多边形的每个内角都相等,且内角是外角的3倍,那么这个多边形的边数是 .
12.一个多边形的每个内角都为144°,那么该正多边形的边数为 .
13.在平行四边形ABCD中,∠BAD=50°,则∠ABC= .
14.如图,在 ABCD中,∠ADO=90°,OA=6cm,OB=3cm,那么AD= cm.
15.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=70°,则∠ACB的大
小为 .
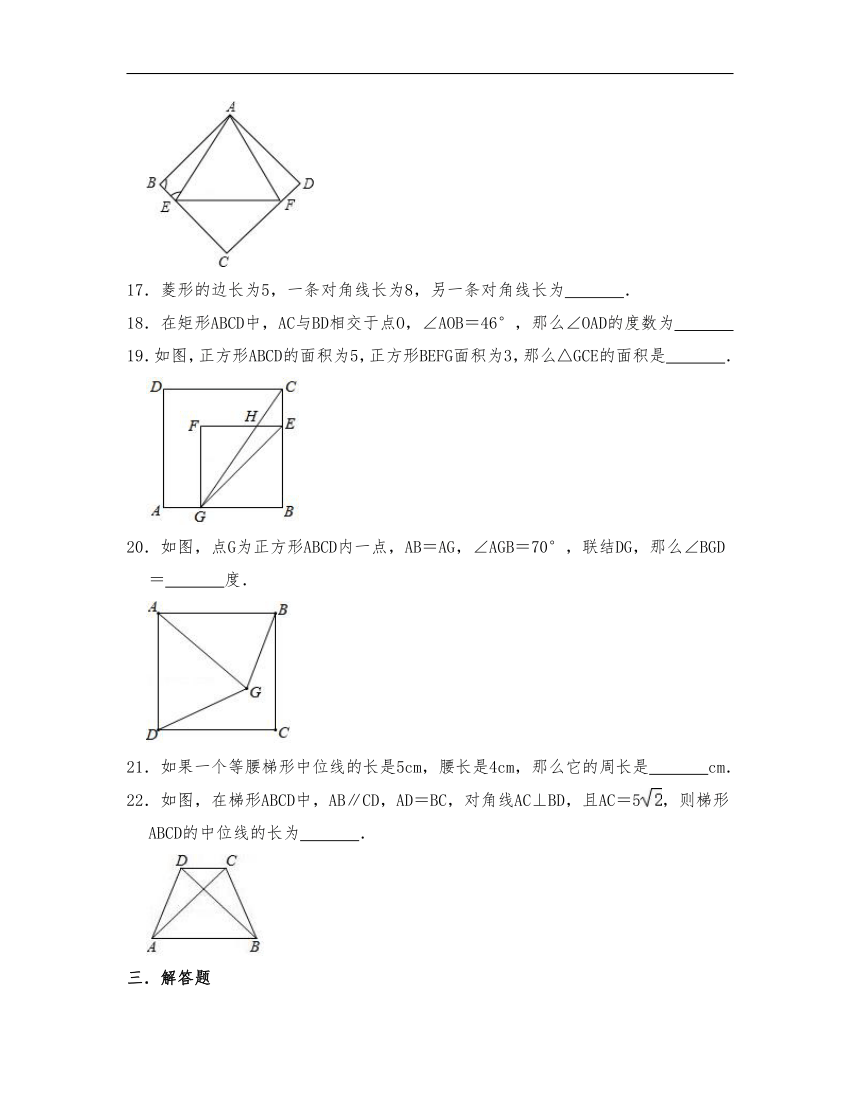
16.如图,四边形ABCD是菱形,点E、F分别在边BC、CD上,且△AEF是等边三角形,AB=AE,则∠B= .
17.菱形的边长为5,一条对角线长为8,另一条对角线长为 .
18.在矩形ABCD中,AC与BD相交于点O,∠AOB=46°,那么∠OAD的度数为
19.如图,正方形ABCD的面积为5,正方形BEFG面积为3,那么△GCE的面积是 .
20.如图,点G为正方形ABCD内一点,AB=AG,∠AGB=70°,联结DG,那么∠BGD= 度.
21.如果一个等腰梯形中位线的长是5cm,腰长是4cm,那么它的周长是 cm.
22.如图,在梯形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,且AC=5,则梯形ABCD的中位线的长为 .
三.解答题
23.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE=BC.
(1)如果AC=6,求AE的长;
(2)设=,=,求向量(用向量、表示).
24.若一个多边形的内角和的比一个四边形的内角和多90°,那么这个多边形的边数是多少?
25.我们知道:三角形的内角和为180°,所以在求四边形的内角和时,我们可以将四边形分割成两个三角形,这样其内角和就是180°×2=360°;同理五边形的内角和是 度;那么n边形的内角和是 度;如果有一个n边形的内角和是1620°,那么n的值是 .
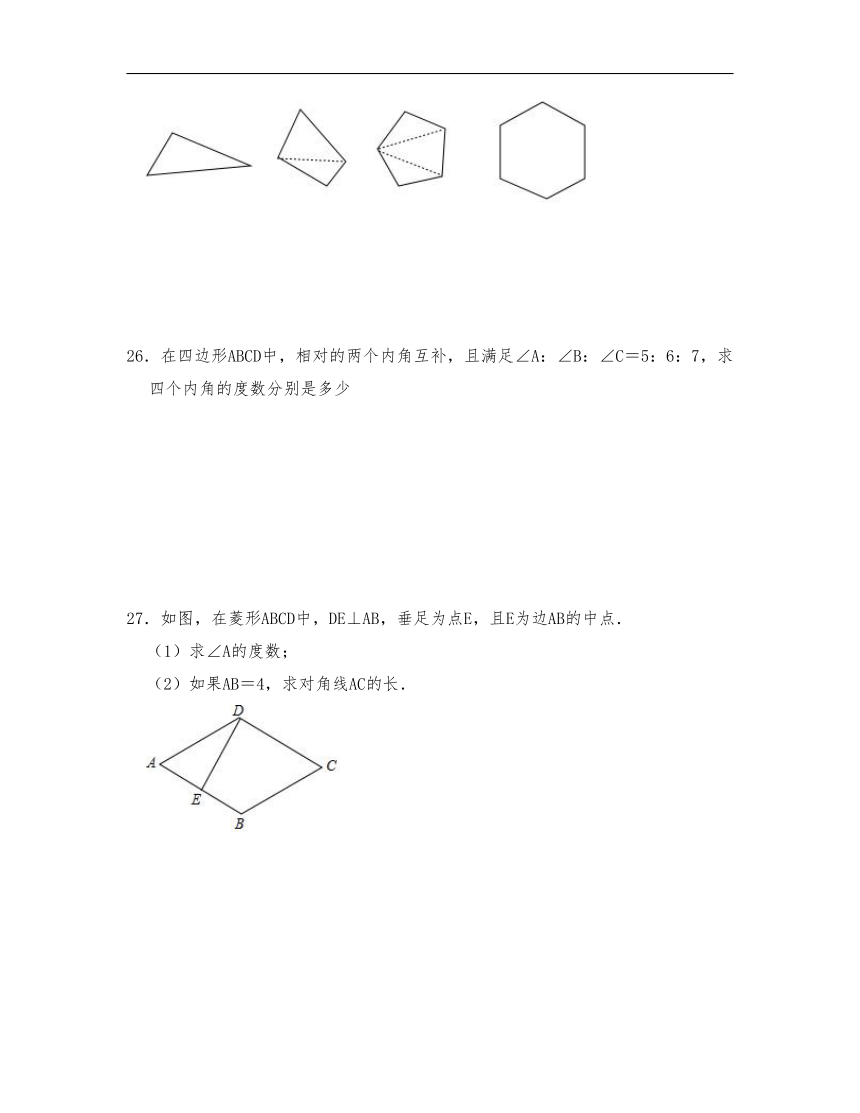
26.在四边形ABCD中,相对的两个内角互补,且满足∠A:∠B:∠C=5:6:7,求四个内角的度数分别是多少
27.如图,在菱形ABCD中,DE⊥AB,垂足为点E,且E为边AB的中点.
(1)求∠A的度数;
(2)如果AB=4,求对角线AC的长.
28.已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD是平行四边形.
29.如图,一次函数y=2x+4的图象与x、y轴分别相交于点A和B,以AB为边作正方形ABCD.
(1)求点A、B、D的坐标.
(2)设点M在x轴上,如果△ABM为等腰三角形,求点M的坐标.
30.如图,矩形ABCD的对角线的交点是O,CE⊥BD,垂足为E,且OE=CE.求:∠DCE的度数.
答案
一.选择题
1.
【分析】利用平行线的判定与性质结合平行四边形的判定得出即可.
【解答】解:如图所示:∵AB∥CD,
∴∠B+∠C=180°,
当∠A=∠C时,则∠A+∠B=180°,
故AD∥BC,
则四边形ABCD是平行四边形.
故选:C.
2.
【分析】根据正多边形的一个内角是144°,则知该正多边形的一个外角为36°,再根据多边形的外角之和为360°,即可求出正多边形的边数.
【解答】解:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数==10,
∴这个正多边形的边数是10.
故选:C.
3.
【分析】根据平面向量的性质逐一判断即可.
【解答】解:∵,,
∴,
故A不符合题意;
∵||=2||不能确定与的方向,
∴不能判定向量与向量平行,
故B符合题意;
∵=2,=3,
∴与方向相同,
∴,
故C不符合题意;
∵+2=0,
∴与方向相反,
∴,
故D不符合题意,
故选:B.
4.
【分析】n边形的内角和为(n﹣2)180°,由此列方程求n的值.
【解答】解:设这个多边形的边数是n,
则(n﹣2)180°=900°,
解得n=7,
故选:B.
5.
【分析】根据平行四边形、菱形、矩形的判定定理即可判断.
【解答】解:对角线互相平分的四边形是平行四边形是平行四边形判定定理,是真命题,故A符合题意;
对角线互相垂直的四边形是菱形是假命题,故B不符合题意;
以一条对角线为对称轴的四边形可能是“筝”形,以一条对角线为对称轴的四边形是菱形是假命题,故C不符合题意;
对称轴互相垂直的四边形是矩形是假命题,故D不符合题意,
故选:A.
6.
【分析】分四边形剪去一个角,边数减少1,不变,增加1,三种情况讨论求出所得多边形的内角和,即可得解.
【解答】解:剪去一个角,若边数减少1,则内角和=(3﹣2) 180°=180°,
若边数不变,则内角和=(4﹣2) 180°=360°,
若边数增加1,则内角和=(5﹣2) 180°=540°,
所以,所得多边形内角和的度数可能是180°,360°,540°,不可能是270°.
故选:B.
7.
【分析】根据题意可以得到:与方向相同,与方向相同.
【解答】解:根据题意知,与方向相同,与方向相同.
A、当向量与方向相反时,=,故本选项不符合题意.
B、当、是两个单位向量方向相同时,=﹣,故本选项不符合题意.
C、由向量=3,=﹣3知,||=||,故本选项符合题意.
D、由向量=3,=﹣3知,||=||,故本选项不符合题意.
故选:C.
8.
【分析】由已知可得该四边形为矩形,再添加条件:一组邻边相等,即可判定为正方形.
【解答】解:由∠A=∠B=∠C=90°可判定四边形ABCD为矩形,
因此再添加条件:一组邻边相等,即可判定四边形ABCD为正方形,
故选:C.
二.填空题
9.
【分析】根据向量的加减计算法则即可得出结果.
【解答】解:∵=,=,
∴
=
=﹣+,
故答案为:﹣+.
10.
【分析】根据多边形的对角线的定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,可知n边形从一个顶点出发可引出(n﹣3)条对角线,据此求解即可.
【解答】解:∵n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线,
∴从七边形的一个顶点出发可以画出7﹣3=4条对角线.
故答案是:4.
11.
【分析】设外角的度数是x,利用外角与相邻内角和为180°求得外角度数,再根据多边形的外角和是360°即可求出多边形的边数.
【解答】解:设多边形的外角的度数是x,则内角是3x,
则x+3x=180°,
解得:x=45°,
则这个多边形的边数是:360°÷45°=8.
故答案为:8.
12.
【分析】根据正多边形的一个内角是144°,则知该正多边形的一个外角为36°,再根据多边形的外角之和为360°,即可求出正多边形的边数.
【解答】解:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数==10,
∴这个正多边形的边数是10.
故答案为:10.
13.
【分析】由平行四边形的性质可得∠BAD+∠ABC=180°,即可求解.
【解答】解:∵四边形ABCD是平行四边形,
∴∠BAD+∠ABC=180°,
∵∠BAD=50°,
∴∠ABC=130°,
故答案为130°.
14.
【分析】由平行四边形的性质可求BO=DO=3cm,由勾股定理可求解.
【解答】解:∵四边形ABCD是平行四边形,
∴BO=DO=3cm,
∵∠ADO=90°,
∴AD===3cm,
故答案为:3.
15.
【分析】先利用矩形的性质得出OA=OB,再根据等腰三角形两底角相等和三角形内角和定理,求出∠BAO=55°,再根据∠ABC=90°﹣∠BAO即可.
【解答】解:∵四边形ABCD是矩形,对角线AC,BD相交于点O,
∴OA=OB,∠ABC=90°,
又∵∠AOB=70°,
∴∠BAO=∠ABO=(180°﹣70°)=55°,
∴∠ACB=90°﹣∠BAO=90°﹣55°=35°.
方法二:矩形ABCD中,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ACB=∠AOB=×70°=35°.
故答案为:35°.
16.
【分析】因为等边三角形△AEF的边长与菱形ABCD的边长相等,所以AB=AE,AF=AD,根据邻角之和为180°即可求得∠B的度数.
【解答】解:∵△AEF的边长与菱形ABCD的边长相等,
∴AB=AE,AF=AD,
设∠B=x,则∠BAD=180°﹣x,
∠BAE=∠DAF=180°﹣2x,
又∵∠BAE+∠EAF+∠FAD=∠BAD
即180°﹣2x+180°﹣2x+60°=180°﹣x
解得x=80°,
故答案为:80°
17.
【分析】根据菱形的性质及勾股定理即可求得另一条对角线的长.
【解答】解:∵菱形的两条对角线互相垂直平分,
根据勾股定理,可求得,另一对角线的一半为3,
则另一条对角线长为6.
故答案为6.
18.
【分析】根据矩形的性质可得∠OAD=∠ODA,再根据三角形的外角性质可得∠AOB=∠OAD+∠ODA=46°,从而可求∠OAD度数.
【解答】解:∵四边形ABCD是矩形,
∴AO=OD,
所以∠OAD=∠ODA.
∵∠AOB=∠OAD+∠ODA=46°,
∴∠OAD=46°÷2=23°.
故答案为23°.
19.
【分析】由正方形的性质可得AB=BC=,BG=BE=,由三角形面积公式可求解.
【解答】解:∵正方形ABCD的面积为5,正方形BEFG面积为3,
∴AB=BC=,BG=BE=
∴CE=﹣
∴△GCE的面积=×CE×BG=×(﹣)×=
故答案为:
20.
【分析】根据正方形的性质可得出AB=AD、∠BAD=90°,由AB=AG、∠AGB=70°利用等腰三角形的性质及三角形内角和定理可求出∠BAG的度数,由∠DAG=90°﹣∠BAG可求出∠DAG的度数,由等腰三角形的性质结合三角形内角和定理可求出∠AGD的度数,再由∠BGD=∠AGB+∠AGD可求出∠BGD的度数.
【解答】解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°.
∵AB=AG,∠AGB=70°,
∴∠BAG=180°﹣70°﹣70°=40°,
∴∠DAG=90°﹣∠BAG=50°,
∴∠AGD=(180°﹣∠DAG)=65°,
∴∠BGD=∠AGB+∠AGD=135°.
故答案为:135.
21.
【分析】根据梯形中位线定理求出梯形的上底+下底,根据梯形的周长公式计算,得到答案.
【解答】解:∵梯形中位线的长是5,
∴梯形的上底+下底=10,
∴等腰梯形的周长=10+4+4=18(cm),
故答案为:18.
22.
【分析】首先求出△ACE是等腰直角三角形,然后根据等腰直角三角形的直角边的长求得斜边的长,从而利用中位线定义求得答案.
【解答】解:过C作CE∥BD交AB的延长线于E,
∵AB∥CD,CE∥BD,
∴四边形DBEC是平行四边形,
∴CE=BD,BE=CD
∵等腰梯形ABCD中,AC=BD∴CE=AC
∵AC⊥BD,CE∥BD,
∴CE⊥AC
∴△ACE是等腰直角三角形,
∵AC=5,
∴AE=AB+BE=AB+CD=AC=10,
∴梯形的中位线=AE=5,
故答案为:5.
三.解答题
23.解:(1)如图,∵DE∥BC,且DE=BC,
∴==.
又AC=6,
∴AE=4.
(2)∵=,=,
∴=﹣=﹣.
又DE∥BC,DE=BC,
∴==(﹣).
24.解:设这个多边形的边数是n,
由题意得:(n﹣2)×180°=360°+90°,
解得:n=12,
答:这个多边形的边数是12.
25.解:180°×(5﹣2)=540°;
180°(n﹣2)=(180n﹣360)°;
∵(n﹣2)×180°=1620°,
∴n﹣2=9,
∴n=11,
故答案为:540;(180n﹣360);11.
26.解:∵四边形ABCD的相对的两个内角互补,∠A:∠B:∠C=5:6:7,
∴∠A=180°×=75°,
∴∠C=180°﹣75°=105°,
∴∠B=∠A=90°,
∴∠D=180°﹣90°=90°.
故答案为:75°,90°,105°,90°.
27.解:连接AC,BD
(1)∵四边形ABCD是菱形
∴AD=AB
∵E是AB中点,DE⊥AB
∴AD=DB
∴AD=DB=AB
∴△ADB是等边三角形
∴∠A=60°
(2)∵四边形ABCD是菱形
∴AC⊥BD,∠DAC=∠DAB=30°,AO=CO,DO=BO
∵AD=BA=4
∴DO=2,AO=DO=2
∴AC=4
28.证明:∵∠D=∠DCE,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形.
29.解:(1)∵当y=0时,2x+4=0,x=﹣2.
∴点A(﹣2,0).
∵当x=0时,y=4.
∴点B(0,4).
过D作DH⊥x轴于H点,
∵四边形ABCD是正方形,
∴∠BAD=∠AOB=∠AHD=90°,AB=AD.
∴∠BAO+∠ABO=∠BAO+∠DAH,
∴∠ABO=∠DAH.
∴△ABO≌△DAH.
∴DH=AO=2,AH=BO=4,
∴OH=AH﹣AO=2.
∴点D(2,﹣2).
(2)∵A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∴AB=2,
①当AB=MB时,
∵OB⊥AM,
∴OM=OA=2,
∴M(2,0);
②当AB=AM时,则OM=OA+AM=2+2,
∴M(﹣2﹣2,0);
③当AB=AM时,则AM=AB=2,
∴OM=AM﹣OA=2﹣2,
∴M(2﹣2,0).
④当MB=MA,可得M(3,0),
综上,M点的坐标为(2,0)或(﹣2﹣2,0)或(2﹣2,0)或(3,0).
30.解:∵四边形ABCD为矩形,
∴∠BCD=90°,OC=OD,
∵CE⊥BD,垂足为E,且OE=CE,
∴∠DOC=∠ECO=45°,
∴∠DCO==67.5°,
∴∠DCE=∠DCO﹣∠OCE=22.5°,
一.选择题
1.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
2.正多边形的一个内角为144°,那么该正多边形的边数为( )
A.8 B.9 C.10 D.11
3.已知非零向量,,,下列条件中,不能判定向量与向量平行的是( )
A.∥,∥ B.||=2|| C.=2,=3 D.+2=
4.如果一个多边形的内角和等于900°,那么这个多边形的边数是( )
A.6 B.7 C.8 D.9
5.下列四个命题中,真命题是( )
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.以一条对角线为对称轴的四边形是菱形
D.对称轴互相垂直的四边形是矩形
6.如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是( )
A.180° B.270° C.360° D.540°
7.已知、是两个单位向量,向量=3,=﹣3,那么下列结论正确的是( )
A.= B.=﹣ C.||=|| D.||=﹣||
8.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
二.填空题
9.如图,已知平行四边形ABCD的对角线AC与BD交于点O.设=,=,那么向量关于向量、的分解式是 .
10.从七边形的一个顶点出发可以画出 条对角线.
11.如果一个多边形的每个内角都相等,且内角是外角的3倍,那么这个多边形的边数是 .
12.一个多边形的每个内角都为144°,那么该正多边形的边数为 .
13.在平行四边形ABCD中,∠BAD=50°,则∠ABC= .
14.如图,在 ABCD中,∠ADO=90°,OA=6cm,OB=3cm,那么AD= cm.
15.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=70°,则∠ACB的大
小为 .
16.如图,四边形ABCD是菱形,点E、F分别在边BC、CD上,且△AEF是等边三角形,AB=AE,则∠B= .
17.菱形的边长为5,一条对角线长为8,另一条对角线长为 .
18.在矩形ABCD中,AC与BD相交于点O,∠AOB=46°,那么∠OAD的度数为
19.如图,正方形ABCD的面积为5,正方形BEFG面积为3,那么△GCE的面积是 .
20.如图,点G为正方形ABCD内一点,AB=AG,∠AGB=70°,联结DG,那么∠BGD= 度.
21.如果一个等腰梯形中位线的长是5cm,腰长是4cm,那么它的周长是 cm.
22.如图,在梯形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,且AC=5,则梯形ABCD的中位线的长为 .
三.解答题
23.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE=BC.
(1)如果AC=6,求AE的长;
(2)设=,=,求向量(用向量、表示).
24.若一个多边形的内角和的比一个四边形的内角和多90°,那么这个多边形的边数是多少?
25.我们知道:三角形的内角和为180°,所以在求四边形的内角和时,我们可以将四边形分割成两个三角形,这样其内角和就是180°×2=360°;同理五边形的内角和是 度;那么n边形的内角和是 度;如果有一个n边形的内角和是1620°,那么n的值是 .
26.在四边形ABCD中,相对的两个内角互补,且满足∠A:∠B:∠C=5:6:7,求四个内角的度数分别是多少
27.如图,在菱形ABCD中,DE⊥AB,垂足为点E,且E为边AB的中点.
(1)求∠A的度数;
(2)如果AB=4,求对角线AC的长.
28.已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD是平行四边形.
29.如图,一次函数y=2x+4的图象与x、y轴分别相交于点A和B,以AB为边作正方形ABCD.
(1)求点A、B、D的坐标.
(2)设点M在x轴上,如果△ABM为等腰三角形,求点M的坐标.
30.如图,矩形ABCD的对角线的交点是O,CE⊥BD,垂足为E,且OE=CE.求:∠DCE的度数.
答案
一.选择题
1.
【分析】利用平行线的判定与性质结合平行四边形的判定得出即可.
【解答】解:如图所示:∵AB∥CD,
∴∠B+∠C=180°,
当∠A=∠C时,则∠A+∠B=180°,
故AD∥BC,
则四边形ABCD是平行四边形.
故选:C.
2.
【分析】根据正多边形的一个内角是144°,则知该正多边形的一个外角为36°,再根据多边形的外角之和为360°,即可求出正多边形的边数.
【解答】解:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数==10,
∴这个正多边形的边数是10.
故选:C.
3.
【分析】根据平面向量的性质逐一判断即可.
【解答】解:∵,,
∴,
故A不符合题意;
∵||=2||不能确定与的方向,
∴不能判定向量与向量平行,
故B符合题意;
∵=2,=3,
∴与方向相同,
∴,
故C不符合题意;
∵+2=0,
∴与方向相反,
∴,
故D不符合题意,
故选:B.
4.
【分析】n边形的内角和为(n﹣2)180°,由此列方程求n的值.
【解答】解:设这个多边形的边数是n,
则(n﹣2)180°=900°,
解得n=7,
故选:B.
5.
【分析】根据平行四边形、菱形、矩形的判定定理即可判断.
【解答】解:对角线互相平分的四边形是平行四边形是平行四边形判定定理,是真命题,故A符合题意;
对角线互相垂直的四边形是菱形是假命题,故B不符合题意;
以一条对角线为对称轴的四边形可能是“筝”形,以一条对角线为对称轴的四边形是菱形是假命题,故C不符合题意;
对称轴互相垂直的四边形是矩形是假命题,故D不符合题意,
故选:A.
6.
【分析】分四边形剪去一个角,边数减少1,不变,增加1,三种情况讨论求出所得多边形的内角和,即可得解.
【解答】解:剪去一个角,若边数减少1,则内角和=(3﹣2) 180°=180°,
若边数不变,则内角和=(4﹣2) 180°=360°,
若边数增加1,则内角和=(5﹣2) 180°=540°,
所以,所得多边形内角和的度数可能是180°,360°,540°,不可能是270°.
故选:B.
7.
【分析】根据题意可以得到:与方向相同,与方向相同.
【解答】解:根据题意知,与方向相同,与方向相同.
A、当向量与方向相反时,=,故本选项不符合题意.
B、当、是两个单位向量方向相同时,=﹣,故本选项不符合题意.
C、由向量=3,=﹣3知,||=||,故本选项符合题意.
D、由向量=3,=﹣3知,||=||,故本选项不符合题意.
故选:C.
8.
【分析】由已知可得该四边形为矩形,再添加条件:一组邻边相等,即可判定为正方形.
【解答】解:由∠A=∠B=∠C=90°可判定四边形ABCD为矩形,
因此再添加条件:一组邻边相等,即可判定四边形ABCD为正方形,
故选:C.
二.填空题
9.
【分析】根据向量的加减计算法则即可得出结果.
【解答】解:∵=,=,
∴
=
=﹣+,
故答案为:﹣+.
10.
【分析】根据多边形的对角线的定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,可知n边形从一个顶点出发可引出(n﹣3)条对角线,据此求解即可.
【解答】解:∵n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线,
∴从七边形的一个顶点出发可以画出7﹣3=4条对角线.
故答案是:4.
11.
【分析】设外角的度数是x,利用外角与相邻内角和为180°求得外角度数,再根据多边形的外角和是360°即可求出多边形的边数.
【解答】解:设多边形的外角的度数是x,则内角是3x,
则x+3x=180°,
解得:x=45°,
则这个多边形的边数是:360°÷45°=8.
故答案为:8.
12.
【分析】根据正多边形的一个内角是144°,则知该正多边形的一个外角为36°,再根据多边形的外角之和为360°,即可求出正多边形的边数.
【解答】解:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数==10,
∴这个正多边形的边数是10.
故答案为:10.
13.
【分析】由平行四边形的性质可得∠BAD+∠ABC=180°,即可求解.
【解答】解:∵四边形ABCD是平行四边形,
∴∠BAD+∠ABC=180°,
∵∠BAD=50°,
∴∠ABC=130°,
故答案为130°.
14.
【分析】由平行四边形的性质可求BO=DO=3cm,由勾股定理可求解.
【解答】解:∵四边形ABCD是平行四边形,
∴BO=DO=3cm,
∵∠ADO=90°,
∴AD===3cm,
故答案为:3.
15.
【分析】先利用矩形的性质得出OA=OB,再根据等腰三角形两底角相等和三角形内角和定理,求出∠BAO=55°,再根据∠ABC=90°﹣∠BAO即可.
【解答】解:∵四边形ABCD是矩形,对角线AC,BD相交于点O,
∴OA=OB,∠ABC=90°,
又∵∠AOB=70°,
∴∠BAO=∠ABO=(180°﹣70°)=55°,
∴∠ACB=90°﹣∠BAO=90°﹣55°=35°.
方法二:矩形ABCD中,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ACB=∠AOB=×70°=35°.
故答案为:35°.
16.
【分析】因为等边三角形△AEF的边长与菱形ABCD的边长相等,所以AB=AE,AF=AD,根据邻角之和为180°即可求得∠B的度数.
【解答】解:∵△AEF的边长与菱形ABCD的边长相等,
∴AB=AE,AF=AD,
设∠B=x,则∠BAD=180°﹣x,
∠BAE=∠DAF=180°﹣2x,
又∵∠BAE+∠EAF+∠FAD=∠BAD
即180°﹣2x+180°﹣2x+60°=180°﹣x
解得x=80°,
故答案为:80°
17.
【分析】根据菱形的性质及勾股定理即可求得另一条对角线的长.
【解答】解:∵菱形的两条对角线互相垂直平分,
根据勾股定理,可求得,另一对角线的一半为3,
则另一条对角线长为6.
故答案为6.
18.
【分析】根据矩形的性质可得∠OAD=∠ODA,再根据三角形的外角性质可得∠AOB=∠OAD+∠ODA=46°,从而可求∠OAD度数.
【解答】解:∵四边形ABCD是矩形,
∴AO=OD,
所以∠OAD=∠ODA.
∵∠AOB=∠OAD+∠ODA=46°,
∴∠OAD=46°÷2=23°.
故答案为23°.
19.
【分析】由正方形的性质可得AB=BC=,BG=BE=,由三角形面积公式可求解.
【解答】解:∵正方形ABCD的面积为5,正方形BEFG面积为3,
∴AB=BC=,BG=BE=
∴CE=﹣
∴△GCE的面积=×CE×BG=×(﹣)×=
故答案为:
20.
【分析】根据正方形的性质可得出AB=AD、∠BAD=90°,由AB=AG、∠AGB=70°利用等腰三角形的性质及三角形内角和定理可求出∠BAG的度数,由∠DAG=90°﹣∠BAG可求出∠DAG的度数,由等腰三角形的性质结合三角形内角和定理可求出∠AGD的度数,再由∠BGD=∠AGB+∠AGD可求出∠BGD的度数.
【解答】解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°.
∵AB=AG,∠AGB=70°,
∴∠BAG=180°﹣70°﹣70°=40°,
∴∠DAG=90°﹣∠BAG=50°,
∴∠AGD=(180°﹣∠DAG)=65°,
∴∠BGD=∠AGB+∠AGD=135°.
故答案为:135.
21.
【分析】根据梯形中位线定理求出梯形的上底+下底,根据梯形的周长公式计算,得到答案.
【解答】解:∵梯形中位线的长是5,
∴梯形的上底+下底=10,
∴等腰梯形的周长=10+4+4=18(cm),
故答案为:18.
22.
【分析】首先求出△ACE是等腰直角三角形,然后根据等腰直角三角形的直角边的长求得斜边的长,从而利用中位线定义求得答案.
【解答】解:过C作CE∥BD交AB的延长线于E,
∵AB∥CD,CE∥BD,
∴四边形DBEC是平行四边形,
∴CE=BD,BE=CD
∵等腰梯形ABCD中,AC=BD∴CE=AC
∵AC⊥BD,CE∥BD,
∴CE⊥AC
∴△ACE是等腰直角三角形,
∵AC=5,
∴AE=AB+BE=AB+CD=AC=10,
∴梯形的中位线=AE=5,
故答案为:5.
三.解答题
23.解:(1)如图,∵DE∥BC,且DE=BC,
∴==.
又AC=6,
∴AE=4.
(2)∵=,=,
∴=﹣=﹣.
又DE∥BC,DE=BC,
∴==(﹣).
24.解:设这个多边形的边数是n,
由题意得:(n﹣2)×180°=360°+90°,
解得:n=12,
答:这个多边形的边数是12.
25.解:180°×(5﹣2)=540°;
180°(n﹣2)=(180n﹣360)°;
∵(n﹣2)×180°=1620°,
∴n﹣2=9,
∴n=11,
故答案为:540;(180n﹣360);11.
26.解:∵四边形ABCD的相对的两个内角互补,∠A:∠B:∠C=5:6:7,
∴∠A=180°×=75°,
∴∠C=180°﹣75°=105°,
∴∠B=∠A=90°,
∴∠D=180°﹣90°=90°.
故答案为:75°,90°,105°,90°.
27.解:连接AC,BD
(1)∵四边形ABCD是菱形
∴AD=AB
∵E是AB中点,DE⊥AB
∴AD=DB
∴AD=DB=AB
∴△ADB是等边三角形
∴∠A=60°
(2)∵四边形ABCD是菱形
∴AC⊥BD,∠DAC=∠DAB=30°,AO=CO,DO=BO
∵AD=BA=4
∴DO=2,AO=DO=2
∴AC=4
28.证明:∵∠D=∠DCE,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形.
29.解:(1)∵当y=0时,2x+4=0,x=﹣2.
∴点A(﹣2,0).
∵当x=0时,y=4.
∴点B(0,4).
过D作DH⊥x轴于H点,
∵四边形ABCD是正方形,
∴∠BAD=∠AOB=∠AHD=90°,AB=AD.
∴∠BAO+∠ABO=∠BAO+∠DAH,
∴∠ABO=∠DAH.
∴△ABO≌△DAH.
∴DH=AO=2,AH=BO=4,
∴OH=AH﹣AO=2.
∴点D(2,﹣2).
(2)∵A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∴AB=2,
①当AB=MB时,
∵OB⊥AM,
∴OM=OA=2,
∴M(2,0);
②当AB=AM时,则OM=OA+AM=2+2,
∴M(﹣2﹣2,0);
③当AB=AM时,则AM=AB=2,
∴OM=AM﹣OA=2﹣2,
∴M(2﹣2,0).
④当MB=MA,可得M(3,0),
综上,M点的坐标为(2,0)或(﹣2﹣2,0)或(2﹣2,0)或(3,0).
30.解:∵四边形ABCD为矩形,
∴∠BCD=90°,OC=OD,
∵CE⊥BD,垂足为E,且OE=CE,
∴∠DOC=∠ECO=45°,
∴∠DCO==67.5°,
∴∠DCE=∠DCO﹣∠OCE=22.5°,
