九年级数学下册试题 期中测试卷(综合能力提升卷)-沪教版(含答案解析)
文档属性
| 名称 | 九年级数学下册试题 期中测试卷(综合能力提升卷)-沪教版(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 794.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 18:27:52 | ||
图片预览




文档简介
期中测试卷(综合能力提升卷)
一、选择题:本题共10个小题,每小题3分,共30分。
1.圆的半径是6cm,若圆心与直线的距离为6.5cm,则直线与圆的位置关系是( )
A.相交或相切 B.相交 C.相切 D.相离
2.若一个点到圆的最小距离为4cm,最大距离为8cm,则该圆的半径是( )
A.2.5cm或6.5cm B.2cm C.6.5cm D.2cm或6cm
3.已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O有公共点( ).
A.0个 B.1个 C.2个 D.无法确定
4.已知正六边形的边长为4,则它的内切圆半径为( )
A.2 B. C. D.4
5.在平面直角坐标系中,以点(2,3)为圆心,3为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
6.如图,AB是的直径,BC是的切线,若,则的大小为( )
A. B. C. D.
7.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A. B. C. D.
8.如图,在⊙O中,AB是⊙O的直径,OB=5,,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①的长度是;②∠CED=∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,点为正六边形对角线上一点,,,则的值是( )
A.20 B.30 C.40 D.随点位置而变化
10.如图,正的边长为,边长为的正的顶点R与点A重合,点P,Q分别在AC,AB上,将沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为( )
A. B. C. D.
二、填空题:本题共8个小题,每题3分,共24分。
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为___.
12.若一个扇形的弧长为π,半径为2,则该扇形的面积为 ___;若一个正多边形的外角为120度,则这个正多边形是正 ___边形.
13.已知的半径为,是线段的中点,若的长为,则点在________.
14.如图,点A,B,C在⊙O上,四边形OABC是平行四边形,若对角线AC=2,则的长为 _____.
15.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心,则折痕的长为______cm.
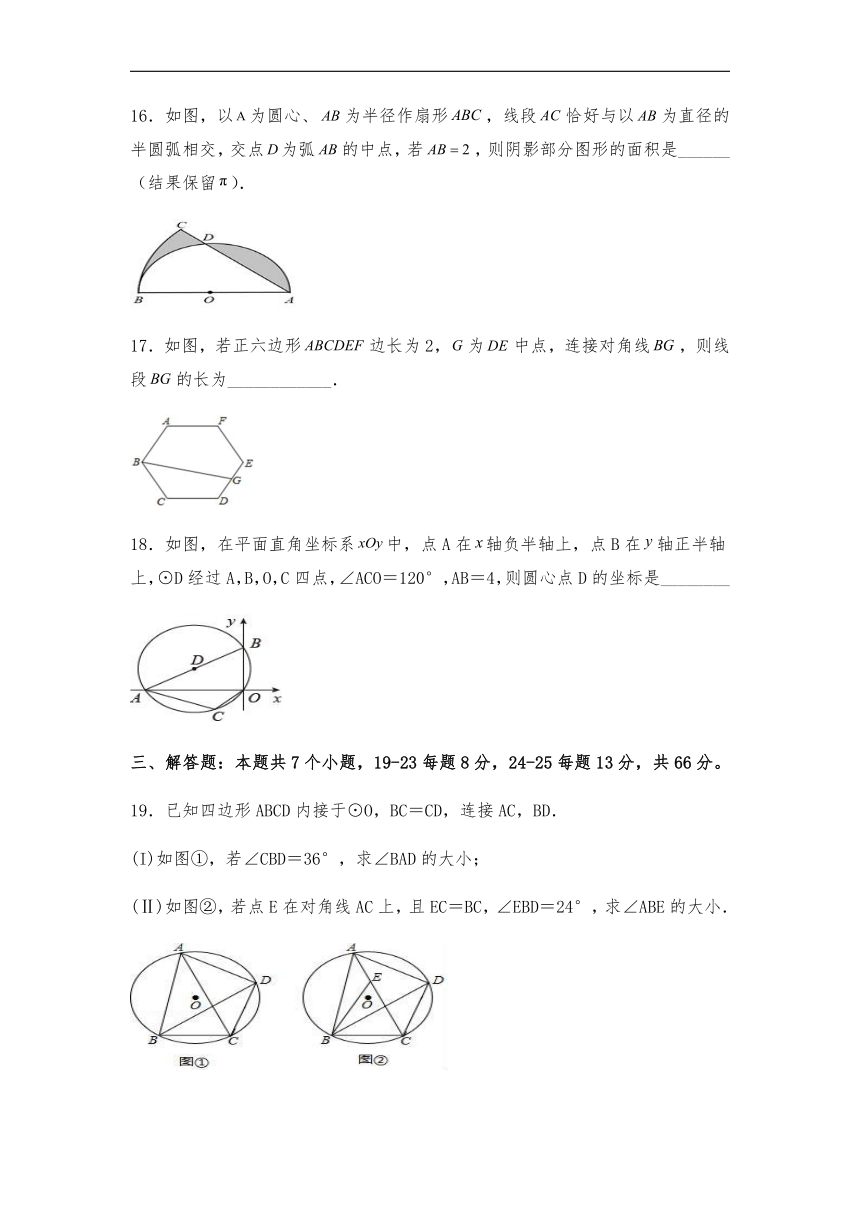
16.如图,以为圆心、为半径作扇形,线段恰好与以为直径的半圆弧相交,交点为弧的中点,若,则阴影部分图形的面积是______(结果保留).
17.如图,若正六边形边长为2,为中点,连接对角线,则线段的长为____________.
18.如图,在平面直角坐标系中,点A在轴负半轴上,点B在轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是________
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.已知四边形ABCD内接于⊙O,BC=CD,连接AC,BD.
(I)如图①,若∠CBD=36°,求∠BAD的大小;
(Ⅱ)如图②,若点E在对角线AC上,且EC=BC,∠EBD=24°,求∠ABE的大小.
20.如图所示,P为⊙O外一点,PA,PB为⊙O的切线,A,B为切点,AC为⊙O的直径,PO交⊙O于点E.
(1)试判断∠APB与∠BAC的数量关系,并说明理由.
(2)若⊙O的半径为4,P是⊙O外一动点,是否存在点P,使四边形PAOB为正方形?若存在,请求出PO的长,并判断点P的个数及其满足的条件;若不存在,请说明理由.
21.如图,在四边形ABCD中,AD∥BC,DA=DC,以点D为圆心,DA的长为半径的⊙D与AB相切于点A,与BC交于点F,过点D作DE⊥BC,垂足为点E.
(1)求证:四边形ABED为矩形;
(2)若AB=4,,求CF的长.
22.如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若AD=,求⊙O的半径.
23.如图,已知是的直径,点D,C是圆上的两个点,且,直线于点E.
(1)求证:是的切线;
(2)若,求阴影部分的面积.
24.如图,为的内接三角形,为的直径,将沿直线折叠得到,交于点.连接交于点,延长和相交于点,过点作交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的值.
25.如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E,交AC于点F,过点C作CG⊥AB交AB于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为⊙O的切线.
(1)求证:BC是⊙O的切线.
(2)求证:=.
(3)若sin∠ABC=,AC=15,求四边形CHQE的面积.
答案
一、选择题。
1.D
【分析】根据圆心与直线的距离大于圆的半径即可判断直线与圆的位置关系
【详解】解:∵圆的半径是6cm,若圆心与直线的距离为6.5cm,
∴直线与圆的位置关系是相离
故选D
2.D
【分析】分两种情况讨论:当点在圆内或点在圆外.
【详解】解:当点在圆内时,圆的直径为4+8=12,圆的半径为6;
当点在圆外,圆的直径为8-4=4,圆的半径为2,
即该圆的半径为2cm或6cm
故选:D.
3.C
【分析】根据⊙O半径为5,点O到直线l的距离为3得到直线l与⊙O相交,即可判断出直线l与⊙O有两个公共点.
【详解】解:∵⊙O半径为5,点O到直线l的距离为3,
∴d<r,
∴直线l与⊙O相交,
∴直线l与⊙O有两个公共点.
故选:C
4.C
【分析】如图所示,连接OA、OB,过点O作OG⊥AB于G,先求出∠AOB=60°,得到△OAB是等边三角形,然后根据勾股定理和三线合一定理求出OG的长即可.
【详解】解:如图所示,连接OA、OB,过点O作OG⊥AB于G,
∵六边形ABCDEF是边长为4的正六边形,
∴,
∴△OAB是等边三角形,
∴OA=AB=4,
∵OG⊥AB,
∴,
∴,
∴边长为4的正六边形的内切圆的半径为:2.
故选C.
5.B
【分析】由已知点(2,3)可求该点到x轴,y轴的距离,再与半径比较,确定圆与坐标轴的位置关系.设d为直线与圆的距离,r为圆的半径,则有若dr,则直线与圆相离.
【详解】解:∵点(2,3)到x轴的距离是3,等于半径,
到y轴的距离是2,小于半径,
∴圆与y轴相交,与x轴相切.
故选B.
6.C
【分析】根据切线的性质,得∠ABC=90°,再根据直角三角形的性质,即可求解.
【详解】解:∵AB是的直径,BC是的切线,
∴AB⊥BC,即∠ABC=90°,
∵,
∴=90°-35°=55°,
故选C.
7.B
【分析】过点O作,,设圆的半径为r,根据垂径定理可得△OBM与△ODN是直角三角形,根据三角函数值进行求解即可得到结果.
【详解】解:如图,过点O作,,设圆的半径为r,
∴△OBM与△ODN是直角三角形,,
∵等边三角形ABC和正方形ADEF都内接于,
∴,,
∴,,
∴,,
∴.
故选B.
8.C
【分析】根据和点是点关于的对称点,求出,求出,即可判断①②;根据圆周角定理求出当和重合时即可判断③;求出点的位置,根据圆周角定理得出此时是直径,即可求出长,即可判断④.
【详解】解:,点是点关于的对称点,
,
,
的长度是,
①正确;
,
②正确;
的度数是,
的度数是,
只有当和重合时,,
,
只有和重合时,,
③错误;
作关于的对称点,连接,交于,连接交于,此时的值最短,等于长,
连接,
,并且弧的度数都是,
,,
,
是的直径,
即,
的最小值是10,
④正确;
综上所述,正确的个数是3个.
故选:.
9.B
【分析】连接AC、AD、CF,AD与CF交于点M,可知M是正六边形的中心,根据矩形的性质求出,再求出正六边形面积即可.
【详解】解:连接AC、AD、CF,AD与CF交于点M,可知M是正六边形的中心,
∵多边形是正六边形,
∴AB=BC,∠B=∠BAF= 120°,
∴∠BAC=30°,
∴∠FAC=90°,
同理,∠DCA=∠FDC=∠DFA=90°,
∴四边形ACDF是矩形,
,,
,
故选:B.
10.B
【分析】从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,第二次是以点P为圆心,所以没有路程,同理在AC和BC上也是相同的情况,由此求解即可.
【详解】解:从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,所以弧长=,第二次是以点P为圆心,所以没有路程,在BC边上,第一次,第二次同样没有路程,AC边上也是如此,点P运动路径的长为×3=2π.
故选:B.
二、填空题。
11.4或2cm
【分析】当点在圆外时,最长距离-最短距离=直径,当点在圆内时,最长距离+最短距离=直径,即可求解..
【详解】解:(1)当点在圆外时,⊙O外一点P到⊙O上一点的距离最长为6cm,最短为2cm,则圆的直径为4cm,那么半径为2cm.
(2)当点在圆内时,⊙O外一点P到⊙O上一点的距离最长为6cm,最短为2cm,则圆的直径为8cm,那么半径为4cm.
故答案为4或2.
12. 三
【分析】根据扇形的面积,计算即可;多边形的外角和等于360°,因为所给多边形的每个外角均相等,据此即可求得正多边形的边数,进而求解.
【详解】解:由题意,,
∴这个正多边形是正三边形.
故答案为:,三.
13.外
【分析】由是线段的中点求出的长,然后与半径作比较即可得出答案.
【详解】解:是线段的中点,
,
的半径为,
,
点在外.
故答案为:外.
14.
【分析】连接OB,交AC于点D,根据有一组邻边相等的平行四边形是菱形,可得四边形OABC为菱形,根据菱形的性质可得:,,,根据等边三角形的判定得出为等边三角形,由此得出,在直角三角形中利用勾股定理即可确定圆的半径,然后代入弧长公式求解即可.
【详解】解:如图所示,连接OB,交AC于点D,
∵四边形OABC为平行四边形,,
∴四边形OABC为菱形,
∴,,,
∵,
∴为等边三角形,
∴,
∴,
在中,设,则,
∴,
即,
解得:或(舍去),
∴的长为:,
故答案为:.
15.
【分析】在图中构建直角三角形,先根据勾股定理得AD的长,再根据垂径定理得AB的长.
【详解】解:作OD⊥AB于D,连接OA.
根据题意得:OD=OA=1cm,
再根据勾股定理得:AD=cm,
根据垂径定理得:AB=2cm.
故答案为:.
16.
【分析】连接DO,根据题意,可知∠DAO=45°,∠DOA=90°,再根据图形可知阴影部分的面积是扇形CAB的面积减去扇形BOD与△AOD的面积之和再加扇形AOD的面积减△AOD的面积,然后代入数据计算即可.
【详解】解:连接DO,
∵线段AC交以AB为直径的半圆弧的中点D,AB=2,
∴∠DAO=45°,∠DOA=90°,DO=AO=1,
∴阴影部分的面积是:( -)+(-)=,
故答案为:.
17.
【分析】过A作AM⊥BE于M,过F作FN⊥BE于N,过G作GH⊥BE于H,由含30°直角三角形的性质结合矩形的性质求出BE,GH,EH,根据勾股定理即可求出BG.
【详解】解:连接,过作于,过作于,过作于,则,
∴四边形是矩形,
∴,,
∵,
∴,
∴,
同理:,
∴,
∵∠GEB=,
∴,
∵为中点,
∴GE=1,
在中,,GE=1,
∴GE=,
由勾股定理可得:,
∴,
在中,由勾股定理可得:.
故答案为:
18.D(,1)
【分析】先利用圆内接四边形的性质得到∠ABO=60°,再根据圆周角定理得到AB为⊙D的直径,则D点为AB的中点,接着利用含30度的直角三角形三边的关系得到OB=2,OA=2,所以A( 2,0),B(0,2),然后利用线段的中点坐标公式得到D点坐标.
【详解】解:∵四边形ABOC为圆的内接四边形,
∴∠ABO+∠ACO=180°,
∴∠ABO=180° 120°=60°,
∵∠AOB=90°,
∴AB为⊙D的直径,
∴D点为AB的中点,
在Rt△ABO中,∵∠ABO=60°,
∴OB=AB=2,
∴OA=OB=2,
∴A( 2,0),B(0,2),
∴D点坐标为( ,1).
故答案为( ,1).
三、解答题。
19.
(1)
∴
∴
∴
(2)
∴
=
∴
∴
20.解:(1)∠APB=2∠BAC.理由:∵PA,PB为⊙O的切线,∴PA=PB,∠APO=∠BPO= ∠APB.易证Rt△PAF≌Rt△PBF,∴∠PFA=∠PFB=90°,∴∠APO+∠PAB=90°.∵PA切⊙O于点A,∴PA⊥OA,即∠BAC+∠PAB=90°,∴∠APO=∠BAC,∴∠APB=2∠BAC.
(2)存在.∵当四边形PAOB是正方形时,PA=AO=OB=BP=4,PO⊥AB且PO=AB,∴PO·AB=PA·PB,即PO2=PA2, PO2=16,∴PO=4 (负值已舍).故这样的点P有无数个,它们到圆心O的距离等于4.
21.
解:(1)∵BA是圆的切线,又DE⊥BC,∴∠BAD=∠BED=90°. 又∵AD∥BC ,∴∠ADE=90°. ∴四边形ABED为矩形.
(2)设AD=3k(k>0),则BC=4k,∴BE=3k,EC=BC-BE=k,DC=AD=3k,又DE2+EC2=DC2,∴42+k2=(3k)2,∴k2=2,∵k>0,∴CF=2EC=2
22.解:(1)证明:在⊙O中,连接,
∵ 直线AB与⊙O相切于点E,
∴ OE⊥AB.
∵ E是AB中点,
∴;
(2)解:∵,
∴ .
∵,
∴AE,AC是⊙O的切线,
∴,(切线长定理)
∴ ,
∵ ,
∴ ,
设⊙O的半径为r,则,
在中,,
∴ ,
在中,
∵,
,
∴ ,
解得,
∴ ⊙O的半径为1.
23.
(1)证明∵,
∴,
∵,
∵,
∴,且是直径,
∴是的切线.
(2)解 连结,,
∵,
∴,
∵,
∴是等边三角形,
∴,
∵是切线,
∴,
∴,
∵,
∴,,
∴
.
24.
(1)证明:∵将沿直线折叠得到,
∴.
∴点在的垂直平分线上.
同理得:点在的垂直平分线上.
∴即,
∵.
∴.
∵是的半径,
∴直线是的切线;
(2)证明:∵为的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
∴,
∴,
∵,
∴;
(3)解:∵,,
∴,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∵,,
∴.
∵,
∴.
∴.
解得:或(舍去).
∴,,
∴.
25.
(1)证明:连接OE,OP,
∵PE⊥AB,点Q为弦EP的中点,
∴AB垂直平分EP,
∴PB=BE,
∵OE=OP,OB=OB,
∴△BEO≌△BPO(SSS),
∴∠BEO=∠BPO,
∵BP为⊙O的切线,
∴∠BPO=90°,
∴∠BEO=90°,
∴OE⊥BC,
∴BC是⊙O的切线.
(2)解:∵∠BEO=∠ACB=90°,
∴AC∥OE,
∴∠CAE=∠OEA,
∵OA=OE,
∴∠EAO=∠AEO,
∴∠CAE=∠EAO,
∴.
(3)解:∵AD为的⊙O直径,点Q为弦EP的中点,
∴EP⊥AB,
∵CG⊥AB,
∴CG∥EP,
∵∠ACB=∠BEO=90°,
∴AC∥OE,
∴∠CAE=∠AEO,
∵OA=OE,
∴∠EAQ=∠AEO,
∴∠CAE=∠EAO,
∵∠ACE=∠AQE=90°,AE=AE,
∴△ACE≌△AQE(AAS),
∴CE=QE,
∵∠AEC+∠CAE=∠EAQ+∠AHG=90°,
∴∠CEH=∠AHG,
∵∠AHG=∠CHE,
∴∠CHE=∠CEH,
∴CH=CE,
∴CH=EQ,
∴四边形CHQE是平行四边形,
∵CH=CE,
∴四边形CHQE是菱形,
∵sin∠ABC═sin∠ACG═=,
∵AC=15,
∴AG=9,
∴CG==12,
∵△ACE≌△AQE,
∴AQ=AC=15,
∴QG=6,
∵HQ2=HG2+QG2,
∴HQ2=(12﹣HQ)2+62,
解得:HQ=,
∴CH=HQ=,
∴四边形CHQE的面积=CH GQ=×6=45.
一、选择题:本题共10个小题,每小题3分,共30分。
1.圆的半径是6cm,若圆心与直线的距离为6.5cm,则直线与圆的位置关系是( )
A.相交或相切 B.相交 C.相切 D.相离
2.若一个点到圆的最小距离为4cm,最大距离为8cm,则该圆的半径是( )
A.2.5cm或6.5cm B.2cm C.6.5cm D.2cm或6cm
3.已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O有公共点( ).
A.0个 B.1个 C.2个 D.无法确定
4.已知正六边形的边长为4,则它的内切圆半径为( )
A.2 B. C. D.4
5.在平面直角坐标系中,以点(2,3)为圆心,3为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
6.如图,AB是的直径,BC是的切线,若,则的大小为( )
A. B. C. D.
7.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A. B. C. D.
8.如图,在⊙O中,AB是⊙O的直径,OB=5,,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①的长度是;②∠CED=∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,点为正六边形对角线上一点,,,则的值是( )
A.20 B.30 C.40 D.随点位置而变化
10.如图,正的边长为,边长为的正的顶点R与点A重合,点P,Q分别在AC,AB上,将沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为( )
A. B. C. D.
二、填空题:本题共8个小题,每题3分,共24分。
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为___.
12.若一个扇形的弧长为π,半径为2,则该扇形的面积为 ___;若一个正多边形的外角为120度,则这个正多边形是正 ___边形.
13.已知的半径为,是线段的中点,若的长为,则点在________.
14.如图,点A,B,C在⊙O上,四边形OABC是平行四边形,若对角线AC=2,则的长为 _____.
15.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心,则折痕的长为______cm.
16.如图,以为圆心、为半径作扇形,线段恰好与以为直径的半圆弧相交,交点为弧的中点,若,则阴影部分图形的面积是______(结果保留).
17.如图,若正六边形边长为2,为中点,连接对角线,则线段的长为____________.
18.如图,在平面直角坐标系中,点A在轴负半轴上,点B在轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是________
三、解答题:本题共7个小题,19-23每题8分,24-25每题13分,共66分。
19.已知四边形ABCD内接于⊙O,BC=CD,连接AC,BD.
(I)如图①,若∠CBD=36°,求∠BAD的大小;
(Ⅱ)如图②,若点E在对角线AC上,且EC=BC,∠EBD=24°,求∠ABE的大小.
20.如图所示,P为⊙O外一点,PA,PB为⊙O的切线,A,B为切点,AC为⊙O的直径,PO交⊙O于点E.
(1)试判断∠APB与∠BAC的数量关系,并说明理由.
(2)若⊙O的半径为4,P是⊙O外一动点,是否存在点P,使四边形PAOB为正方形?若存在,请求出PO的长,并判断点P的个数及其满足的条件;若不存在,请说明理由.
21.如图,在四边形ABCD中,AD∥BC,DA=DC,以点D为圆心,DA的长为半径的⊙D与AB相切于点A,与BC交于点F,过点D作DE⊥BC,垂足为点E.
(1)求证:四边形ABED为矩形;
(2)若AB=4,,求CF的长.
22.如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若AD=,求⊙O的半径.
23.如图,已知是的直径,点D,C是圆上的两个点,且,直线于点E.
(1)求证:是的切线;
(2)若,求阴影部分的面积.
24.如图,为的内接三角形,为的直径,将沿直线折叠得到,交于点.连接交于点,延长和相交于点,过点作交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的值.
25.如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E,交AC于点F,过点C作CG⊥AB交AB于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为⊙O的切线.
(1)求证:BC是⊙O的切线.
(2)求证:=.
(3)若sin∠ABC=,AC=15,求四边形CHQE的面积.
答案
一、选择题。
1.D
【分析】根据圆心与直线的距离大于圆的半径即可判断直线与圆的位置关系
【详解】解:∵圆的半径是6cm,若圆心与直线的距离为6.5cm,
∴直线与圆的位置关系是相离
故选D
2.D
【分析】分两种情况讨论:当点在圆内或点在圆外.
【详解】解:当点在圆内时,圆的直径为4+8=12,圆的半径为6;
当点在圆外,圆的直径为8-4=4,圆的半径为2,
即该圆的半径为2cm或6cm
故选:D.
3.C
【分析】根据⊙O半径为5,点O到直线l的距离为3得到直线l与⊙O相交,即可判断出直线l与⊙O有两个公共点.
【详解】解:∵⊙O半径为5,点O到直线l的距离为3,
∴d<r,
∴直线l与⊙O相交,
∴直线l与⊙O有两个公共点.
故选:C
4.C
【分析】如图所示,连接OA、OB,过点O作OG⊥AB于G,先求出∠AOB=60°,得到△OAB是等边三角形,然后根据勾股定理和三线合一定理求出OG的长即可.
【详解】解:如图所示,连接OA、OB,过点O作OG⊥AB于G,
∵六边形ABCDEF是边长为4的正六边形,
∴,
∴△OAB是等边三角形,
∴OA=AB=4,
∵OG⊥AB,
∴,
∴,
∴边长为4的正六边形的内切圆的半径为:2.
故选C.
5.B
【分析】由已知点(2,3)可求该点到x轴,y轴的距离,再与半径比较,确定圆与坐标轴的位置关系.设d为直线与圆的距离,r为圆的半径,则有若d
【详解】解:∵点(2,3)到x轴的距离是3,等于半径,
到y轴的距离是2,小于半径,
∴圆与y轴相交,与x轴相切.
故选B.
6.C
【分析】根据切线的性质,得∠ABC=90°,再根据直角三角形的性质,即可求解.
【详解】解:∵AB是的直径,BC是的切线,
∴AB⊥BC,即∠ABC=90°,
∵,
∴=90°-35°=55°,
故选C.
7.B
【分析】过点O作,,设圆的半径为r,根据垂径定理可得△OBM与△ODN是直角三角形,根据三角函数值进行求解即可得到结果.
【详解】解:如图,过点O作,,设圆的半径为r,
∴△OBM与△ODN是直角三角形,,
∵等边三角形ABC和正方形ADEF都内接于,
∴,,
∴,,
∴,,
∴.
故选B.
8.C
【分析】根据和点是点关于的对称点,求出,求出,即可判断①②;根据圆周角定理求出当和重合时即可判断③;求出点的位置,根据圆周角定理得出此时是直径,即可求出长,即可判断④.
【详解】解:,点是点关于的对称点,
,
,
的长度是,
①正确;
,
②正确;
的度数是,
的度数是,
只有当和重合时,,
,
只有和重合时,,
③错误;
作关于的对称点,连接,交于,连接交于,此时的值最短,等于长,
连接,
,并且弧的度数都是,
,,
,
是的直径,
即,
的最小值是10,
④正确;
综上所述,正确的个数是3个.
故选:.
9.B
【分析】连接AC、AD、CF,AD与CF交于点M,可知M是正六边形的中心,根据矩形的性质求出,再求出正六边形面积即可.
【详解】解:连接AC、AD、CF,AD与CF交于点M,可知M是正六边形的中心,
∵多边形是正六边形,
∴AB=BC,∠B=∠BAF= 120°,
∴∠BAC=30°,
∴∠FAC=90°,
同理,∠DCA=∠FDC=∠DFA=90°,
∴四边形ACDF是矩形,
,,
,
故选:B.
10.B
【分析】从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,第二次是以点P为圆心,所以没有路程,同理在AC和BC上也是相同的情况,由此求解即可.
【详解】解:从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,所以弧长=,第二次是以点P为圆心,所以没有路程,在BC边上,第一次,第二次同样没有路程,AC边上也是如此,点P运动路径的长为×3=2π.
故选:B.
二、填空题。
11.4或2cm
【分析】当点在圆外时,最长距离-最短距离=直径,当点在圆内时,最长距离+最短距离=直径,即可求解..
【详解】解:(1)当点在圆外时,⊙O外一点P到⊙O上一点的距离最长为6cm,最短为2cm,则圆的直径为4cm,那么半径为2cm.
(2)当点在圆内时,⊙O外一点P到⊙O上一点的距离最长为6cm,最短为2cm,则圆的直径为8cm,那么半径为4cm.
故答案为4或2.
12. 三
【分析】根据扇形的面积,计算即可;多边形的外角和等于360°,因为所给多边形的每个外角均相等,据此即可求得正多边形的边数,进而求解.
【详解】解:由题意,,
∴这个正多边形是正三边形.
故答案为:,三.
13.外
【分析】由是线段的中点求出的长,然后与半径作比较即可得出答案.
【详解】解:是线段的中点,
,
的半径为,
,
点在外.
故答案为:外.
14.
【分析】连接OB,交AC于点D,根据有一组邻边相等的平行四边形是菱形,可得四边形OABC为菱形,根据菱形的性质可得:,,,根据等边三角形的判定得出为等边三角形,由此得出,在直角三角形中利用勾股定理即可确定圆的半径,然后代入弧长公式求解即可.
【详解】解:如图所示,连接OB,交AC于点D,
∵四边形OABC为平行四边形,,
∴四边形OABC为菱形,
∴,,,
∵,
∴为等边三角形,
∴,
∴,
在中,设,则,
∴,
即,
解得:或(舍去),
∴的长为:,
故答案为:.
15.
【分析】在图中构建直角三角形,先根据勾股定理得AD的长,再根据垂径定理得AB的长.
【详解】解:作OD⊥AB于D,连接OA.
根据题意得:OD=OA=1cm,
再根据勾股定理得:AD=cm,
根据垂径定理得:AB=2cm.
故答案为:.
16.
【分析】连接DO,根据题意,可知∠DAO=45°,∠DOA=90°,再根据图形可知阴影部分的面积是扇形CAB的面积减去扇形BOD与△AOD的面积之和再加扇形AOD的面积减△AOD的面积,然后代入数据计算即可.
【详解】解:连接DO,
∵线段AC交以AB为直径的半圆弧的中点D,AB=2,
∴∠DAO=45°,∠DOA=90°,DO=AO=1,
∴阴影部分的面积是:( -)+(-)=,
故答案为:.
17.
【分析】过A作AM⊥BE于M,过F作FN⊥BE于N,过G作GH⊥BE于H,由含30°直角三角形的性质结合矩形的性质求出BE,GH,EH,根据勾股定理即可求出BG.
【详解】解:连接,过作于,过作于,过作于,则,
∴四边形是矩形,
∴,,
∵,
∴,
∴,
同理:,
∴,
∵∠GEB=,
∴,
∵为中点,
∴GE=1,
在中,,GE=1,
∴GE=,
由勾股定理可得:,
∴,
在中,由勾股定理可得:.
故答案为:
18.D(,1)
【分析】先利用圆内接四边形的性质得到∠ABO=60°,再根据圆周角定理得到AB为⊙D的直径,则D点为AB的中点,接着利用含30度的直角三角形三边的关系得到OB=2,OA=2,所以A( 2,0),B(0,2),然后利用线段的中点坐标公式得到D点坐标.
【详解】解:∵四边形ABOC为圆的内接四边形,
∴∠ABO+∠ACO=180°,
∴∠ABO=180° 120°=60°,
∵∠AOB=90°,
∴AB为⊙D的直径,
∴D点为AB的中点,
在Rt△ABO中,∵∠ABO=60°,
∴OB=AB=2,
∴OA=OB=2,
∴A( 2,0),B(0,2),
∴D点坐标为( ,1).
故答案为( ,1).
三、解答题。
19.
(1)
∴
∴
∴
(2)
∴
=
∴
∴
20.解:(1)∠APB=2∠BAC.理由:∵PA,PB为⊙O的切线,∴PA=PB,∠APO=∠BPO= ∠APB.易证Rt△PAF≌Rt△PBF,∴∠PFA=∠PFB=90°,∴∠APO+∠PAB=90°.∵PA切⊙O于点A,∴PA⊥OA,即∠BAC+∠PAB=90°,∴∠APO=∠BAC,∴∠APB=2∠BAC.
(2)存在.∵当四边形PAOB是正方形时,PA=AO=OB=BP=4,PO⊥AB且PO=AB,∴PO·AB=PA·PB,即PO2=PA2, PO2=16,∴PO=4 (负值已舍).故这样的点P有无数个,它们到圆心O的距离等于4.
21.
解:(1)∵BA是圆的切线,又DE⊥BC,∴∠BAD=∠BED=90°. 又∵AD∥BC ,∴∠ADE=90°. ∴四边形ABED为矩形.
(2)设AD=3k(k>0),则BC=4k,∴BE=3k,EC=BC-BE=k,DC=AD=3k,又DE2+EC2=DC2,∴42+k2=(3k)2,∴k2=2,∵k>0,∴CF=2EC=2
22.解:(1)证明:在⊙O中,连接,
∵ 直线AB与⊙O相切于点E,
∴ OE⊥AB.
∵ E是AB中点,
∴;
(2)解:∵,
∴ .
∵,
∴AE,AC是⊙O的切线,
∴,(切线长定理)
∴ ,
∵ ,
∴ ,
设⊙O的半径为r,则,
在中,,
∴ ,
在中,
∵,
,
∴ ,
解得,
∴ ⊙O的半径为1.
23.
(1)证明∵,
∴,
∵,
∵,
∴,且是直径,
∴是的切线.
(2)解 连结,,
∵,
∴,
∵,
∴是等边三角形,
∴,
∵是切线,
∴,
∴,
∵,
∴,,
∴
.
24.
(1)证明:∵将沿直线折叠得到,
∴.
∴点在的垂直平分线上.
同理得:点在的垂直平分线上.
∴即,
∵.
∴.
∵是的半径,
∴直线是的切线;
(2)证明:∵为的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
∴,
∴,
∵,
∴;
(3)解:∵,,
∴,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∵,,
∴.
∵,
∴.
∴.
解得:或(舍去).
∴,,
∴.
25.
(1)证明:连接OE,OP,
∵PE⊥AB,点Q为弦EP的中点,
∴AB垂直平分EP,
∴PB=BE,
∵OE=OP,OB=OB,
∴△BEO≌△BPO(SSS),
∴∠BEO=∠BPO,
∵BP为⊙O的切线,
∴∠BPO=90°,
∴∠BEO=90°,
∴OE⊥BC,
∴BC是⊙O的切线.
(2)解:∵∠BEO=∠ACB=90°,
∴AC∥OE,
∴∠CAE=∠OEA,
∵OA=OE,
∴∠EAO=∠AEO,
∴∠CAE=∠EAO,
∴.
(3)解:∵AD为的⊙O直径,点Q为弦EP的中点,
∴EP⊥AB,
∵CG⊥AB,
∴CG∥EP,
∵∠ACB=∠BEO=90°,
∴AC∥OE,
∴∠CAE=∠AEO,
∵OA=OE,
∴∠EAQ=∠AEO,
∴∠CAE=∠EAO,
∵∠ACE=∠AQE=90°,AE=AE,
∴△ACE≌△AQE(AAS),
∴CE=QE,
∵∠AEC+∠CAE=∠EAQ+∠AHG=90°,
∴∠CEH=∠AHG,
∵∠AHG=∠CHE,
∴∠CHE=∠CEH,
∴CH=CE,
∴CH=EQ,
∴四边形CHQE是平行四边形,
∵CH=CE,
∴四边形CHQE是菱形,
∵sin∠ABC═sin∠ACG═=,
∵AC=15,
∴AG=9,
∴CG==12,
∵△ACE≌△AQE,
∴AQ=AC=15,
∴QG=6,
∵HQ2=HG2+QG2,
∴HQ2=(12﹣HQ)2+62,
解得:HQ=,
∴CH=HQ=,
∴四边形CHQE的面积=CH GQ=×6=45.
同课章节目录
