17.3 一元二次方程根的判别式 课件 (共14张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 17.3 一元二次方程根的判别式 课件 (共14张PPT) 2023-2024学年数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 284.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第17章 一元二次方程
17.3 一元二次方程根的判别式
学习目标
1.理解并掌握一元二次方程根的判别式,能运用判别式,在不解方程的前提下判断一元二次方程根的情况.(重点、难点)
2.通过一元二次方程根的情况的探究过程,体会从特殊到一般、猜想及分类讨论的数学思想,提高观察、分析、归纳的能力.
知识回顾
1.一元二次方程的一般形式是什么?
2.一元二次方程的求根公式是什么?
ax2+bx+c=0 (a≠0)
x=。
知识讲解
一元二次方程ax2+bx+c=0(a≠0)在什么情况下有实数根?在什么情况下没有实数根?与同伴进行交流。
方程ax2+bx+c=0(a≠0)经过配方可以变形为
因为a≠0,所以4a >0,这样由b -4ac就可以确定是正数、零还是负数。
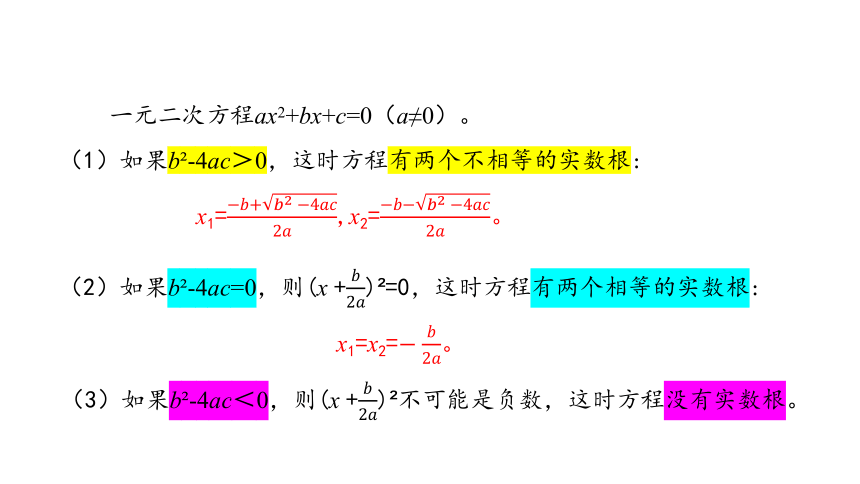
一元二次方程ax2+bx+c=0(a≠0)。
(1)如果b -4ac>0,这时方程有两个不相等的实数根:
x1=,x2=。
x1=x2=。
(3)如果b -4ac<0,则(x +) 不可能是负数,这时方程没有实数根。
(2)如果b -4ac=0,则(x +) =0,这时方程有两个相等的实数根:
以上三个结论反过来也是正确的。
一元二次方程根的判别式:
我们把b2-4ac叫做一元二次方程ax2+bx+c=0 (a≠0)的根的判别式,通常用希腊字母“Δ”来表示,即Δ=b2-4ac。
特别提醒:
(1)确定根的判别式时,需先将方程化为一般形式,确定a,b,c后再计算;
(2)使用一元二次方程根的判别式的前提是二次项系数不为0。
一元二次方程根的个数与根的判别式的关系:
对于一元二次方程ax2+bx+c=0(a≠0):
(1)Δ>0 方程有两个不相等的实数根;
(2)Δ=0 方程有两个相等的实数根;
(3)Δ<0 方程没有实数根。
总结
例 利用一元二次方程的根的判别式,判断下列方程的根的情况:
(1)2x +x-4=0;
例题解读
解:a=2,b=1,c=-4。
因为=b -4ac=1 -4×2×(-4)=33>0,
所以方程有两个不相等的实数根。
例 利用一元二次方程的根的判别式,判断下列方程的根的情况:
(2)4y +9=12y;
例题解读
解:原方程化为一般形式,得4y -12y+9=0。
a=4,b=-12,c=9。
因为=b -4ac=(-12) -4×4×9=0,
所以原方程有两个相等的实数根。
例 利用一元二次方程的根的判别式,判断下列方程的根的情况:
(3)5(t +1)-6t=0。
例题解读
解:原方程化为一般形式,得5t -6t+5=0。
a=5,b=-6,c=5。
因为=b -4ac=(-6) -4×5×5=-64<0,
所以原方程没有实数根。
1. 一元二次方程(x+1)(x-1)=2x+3的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
A
解析:由题意,知原方程可化为x -2x-4=0。
由根的判别式,知b -4ac=(-2) -4×1×(-4)=20>0。
所以原方程有两个不相等的实数根。
随堂演练
2.对于任意实数k,关于x的方程x2-2(k+1)x-k2+2k-1=0的根的情况为( )
A. 有两个相等的实数根 B. 没有实数根
C. 有两个不等的实数根 D. 无法判断
C
解析:由根的判别式,知b -4ac=[2(k+1)] -4×1×(-k2+2k-1)=8k +8>0。
所以原方程有两个不相等的实数根。
3.关于x 的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是( )
A. m≤3 B. m<3
C. m<3且m≠2 D. m≤3且m≠2
D
解析:由题意,知m-2≠0,即m≠2。
由根的判别式,知b -4ac=2 -4×(m-2)×1=12-4m≥0。
解得m≤3。
所以可知m的取值范围是m≤3且m≠2。
课堂小结
根的判别式:Δ = b2 - 4ac
Δ > 0 时,方程有两个不相等的实数根
Δ < 0 时,方程没有实根
Δ = 0 时,方程有两个相等的实根
第17章 一元二次方程
17.3 一元二次方程根的判别式
学习目标
1.理解并掌握一元二次方程根的判别式,能运用判别式,在不解方程的前提下判断一元二次方程根的情况.(重点、难点)
2.通过一元二次方程根的情况的探究过程,体会从特殊到一般、猜想及分类讨论的数学思想,提高观察、分析、归纳的能力.
知识回顾
1.一元二次方程的一般形式是什么?
2.一元二次方程的求根公式是什么?
ax2+bx+c=0 (a≠0)
x=。
知识讲解
一元二次方程ax2+bx+c=0(a≠0)在什么情况下有实数根?在什么情况下没有实数根?与同伴进行交流。
方程ax2+bx+c=0(a≠0)经过配方可以变形为
因为a≠0,所以4a >0,这样由b -4ac就可以确定是正数、零还是负数。
一元二次方程ax2+bx+c=0(a≠0)。
(1)如果b -4ac>0,这时方程有两个不相等的实数根:
x1=,x2=。
x1=x2=。
(3)如果b -4ac<0,则(x +) 不可能是负数,这时方程没有实数根。
(2)如果b -4ac=0,则(x +) =0,这时方程有两个相等的实数根:
以上三个结论反过来也是正确的。
一元二次方程根的判别式:
我们把b2-4ac叫做一元二次方程ax2+bx+c=0 (a≠0)的根的判别式,通常用希腊字母“Δ”来表示,即Δ=b2-4ac。
特别提醒:
(1)确定根的判别式时,需先将方程化为一般形式,确定a,b,c后再计算;
(2)使用一元二次方程根的判别式的前提是二次项系数不为0。
一元二次方程根的个数与根的判别式的关系:
对于一元二次方程ax2+bx+c=0(a≠0):
(1)Δ>0 方程有两个不相等的实数根;
(2)Δ=0 方程有两个相等的实数根;
(3)Δ<0 方程没有实数根。
总结
例 利用一元二次方程的根的判别式,判断下列方程的根的情况:
(1)2x +x-4=0;
例题解读
解:a=2,b=1,c=-4。
因为=b -4ac=1 -4×2×(-4)=33>0,
所以方程有两个不相等的实数根。
例 利用一元二次方程的根的判别式,判断下列方程的根的情况:
(2)4y +9=12y;
例题解读
解:原方程化为一般形式,得4y -12y+9=0。
a=4,b=-12,c=9。
因为=b -4ac=(-12) -4×4×9=0,
所以原方程有两个相等的实数根。
例 利用一元二次方程的根的判别式,判断下列方程的根的情况:
(3)5(t +1)-6t=0。
例题解读
解:原方程化为一般形式,得5t -6t+5=0。
a=5,b=-6,c=5。
因为=b -4ac=(-6) -4×5×5=-64<0,
所以原方程没有实数根。
1. 一元二次方程(x+1)(x-1)=2x+3的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
A
解析:由题意,知原方程可化为x -2x-4=0。
由根的判别式,知b -4ac=(-2) -4×1×(-4)=20>0。
所以原方程有两个不相等的实数根。
随堂演练
2.对于任意实数k,关于x的方程x2-2(k+1)x-k2+2k-1=0的根的情况为( )
A. 有两个相等的实数根 B. 没有实数根
C. 有两个不等的实数根 D. 无法判断
C
解析:由根的判别式,知b -4ac=[2(k+1)] -4×1×(-k2+2k-1)=8k +8>0。
所以原方程有两个不相等的实数根。
3.关于x 的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是( )
A. m≤3 B. m<3
C. m<3且m≠2 D. m≤3且m≠2
D
解析:由题意,知m-2≠0,即m≠2。
由根的判别式,知b -4ac=2 -4×(m-2)×1=12-4m≥0。
解得m≤3。
所以可知m的取值范围是m≤3且m≠2。
课堂小结
根的判别式:Δ = b2 - 4ac
Δ > 0 时,方程有两个不相等的实数根
Δ < 0 时,方程没有实根
Δ = 0 时,方程有两个相等的实根
