17.5 一元二次方程的应用 课件 (共22张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 17.5 一元二次方程的应用 课件 (共22张PPT) 2023-2024学年数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 436.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:25:34 | ||
图片预览






文档简介
(共22张PPT)
第17章 一元二次方程
17.5 一元二次方程的应用
学习目标
1.能够利用一元二次方程解决有关实际问题,并能根据具体问题的实际意义,检验结果的合理性。(重点、难点)
2.认识方程模型的重要性,寻找实际问题中的相等关系。(难点)
3.在问题解决中,经历一定的合作交流活动,进一步发展学生合作交流的意识和能力。
知识讲解
知识点1 平均变化率问题与一元二次方程
填空:
1. 前年生产 1 吨甲种药品的成本是 5000 元,随着生产技术的进步,去年生产 1 吨甲种药品的成本是 4650 元,则下降率是 . 如果保持这个下降率,那么现在生产 1 吨甲种药品的成本是 元.
7%
4324.5
下降率 =
下降前的量 - 下降后的量
下降前的量
探究归纳
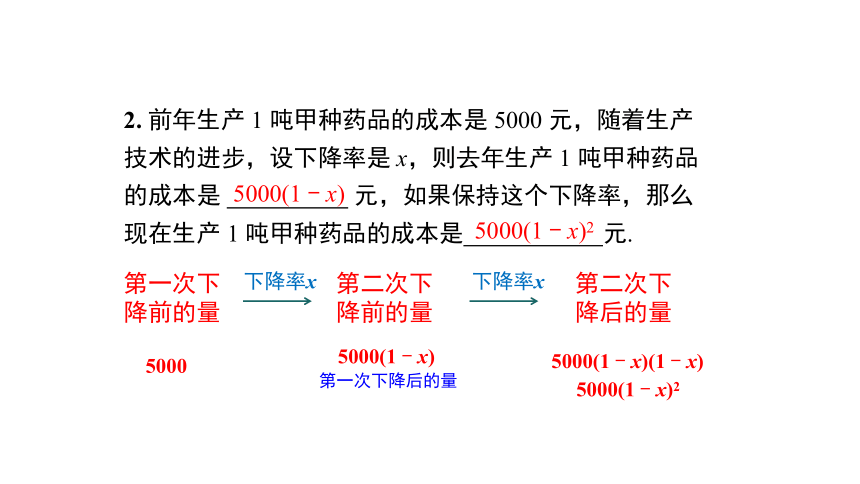
2. 前年生产 1 吨甲种药品的成本是 5000 元,随着生产技术的进步,设下降率是 x,则去年生产 1 吨甲种药品的成本是 元,如果保持这个下降率,那么现在生产 1 吨甲种药品的成本是 元.
下降率x
第一次下降前的量
5000(1 - x)
第一次下降后的量
5000
下降率x
第二次下降后的量
第二次下降前的量
5000(1 - x)(1 - x)
5000(1 - x)2
5000(1 - x)
5000(1 - x)2
例1 前年生产 1 吨甲种药品的成本是 5000 元,随着生产技术的进步,现在生产 1 吨甲种药品的成本是 4050 元,试求甲种药品成本的年平均下降率.
解:设甲种药品的年平均下降率为 x. 根据题意,列方程,得
5 000 (1 - x)2 = 4050,
解方程,得
x1 = 0.1,x2 = 1.9.
根据问题的实际意义,取 x = 0.1,
即甲种药品成本的年平均下降率为10%.
下降率不可为负,且不大于1.
注意
例题解读
例2 某公司去年的各项经营中,一月份的营业额为 200 万元,一月、二月、三月的营业额共 950 万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为 x.根据题意,得
答:这个增长率为 50%.
200 + 200(1 + x) + 200(1 + x)2 = 950.
整理方程,得 4x2 + 12x - 7 = 0.
解得 x1 = -3.5 (舍去),x2 = 0.5.
增长率不可为负,但可以超过 1.
注意
方法归纳
建立一元二次方程模型
实际问题
分析数量关系
设出未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
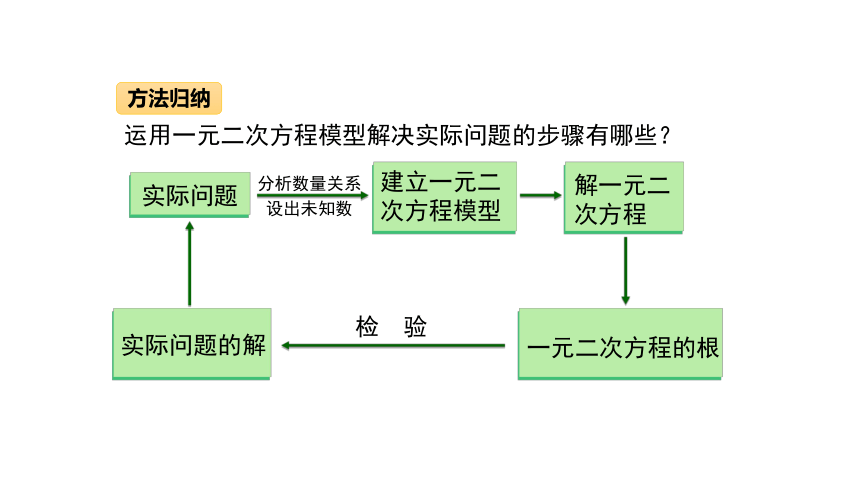
运用一元二次方程模型解决实际问题的步骤有哪些?
知识点2 几何图形与一元二次方程
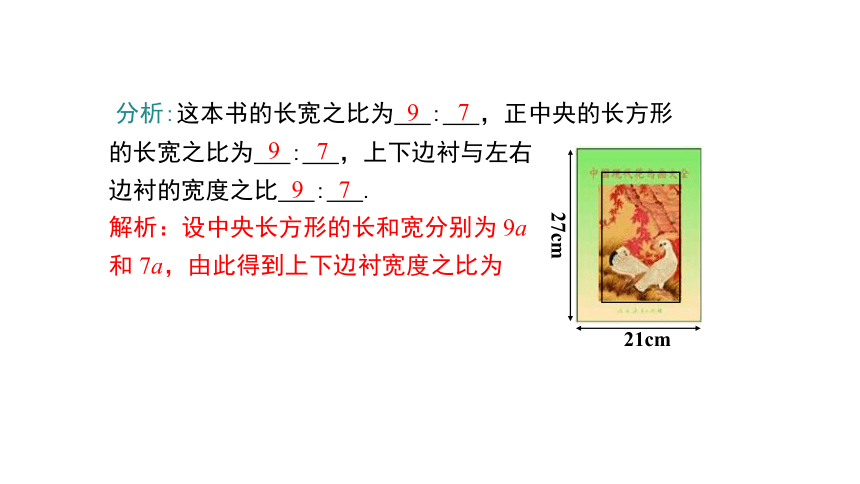
例3 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的长方形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到 0.1 cm)?
27cm
21cm
分析:这本书的长宽之比为 : ,正中央的长方形的长宽之比为 : ,上下边衬与左右
边衬的宽度之比 : .
9
9
解析:设中央长方形的长和宽分别为 9a 和 7a,由此得到上下边衬宽度之比为
9
7
7
7
27cm
21cm
解1:设上下边衬的宽为 9x cm,左右边衬的宽为 7x cm. 依题意得
解得
故上下边衬的宽为
故左右边衬的宽为
方程的哪个根合乎实际意义
为什么
试一试:如果换一种设未知数的方法,是否可以更简单地解决上面的问题?
27cm
21cm
解2:设正中央的长方形的两边别为 9x cm,7x cm. 依题意得
解得
故上下边衬的宽度为
左右边衬的宽度为
27cm
21cm
在几何图形的面积问题中,面积公式往往就是建立等量关系的关键. 如果图形不规则,应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程.
方法点拨
例4 如图,在 Rt△ABC 中,∠C = 90°,AC = 6 cm,BC = 8 cm. 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s 的速度移动;同时点 Q 沿 CB 边从点 C 向终点 B 以 2 cm/s 的速度移动,且当其中一点到达终点时,另一点也随之停止移动. 问点 P,Q 出发几秒后可使 △PCQ 的面积为 9 cm ?
根据题意得 AP = x cm,PC = (6 - x) cm,CQ = 2x cm.
解:设点 P,Q 出发 x s 后 △PCQ 的面积为 9 cm .
整理,得
解得 x1 = x2 = 3.
答:点 P,Q 出发 3 s 后可使△PCQ的面积为 9 cm .
则有
例5 如图,在一块长为 92 m,宽为 60 m 的长方形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为 885 m2 的 6 个长方形小块.水渠应挖多宽?
解:设水渠宽为 x m,将所有耕地拼在一起,变成一个新的长方形,则其长为 (92 - 2x) m,宽为 (60 - x) m. 则有
(92 - 2x)(60 - x) = 6×885.
解得 x1 = 105(舍去),x2 = 1.
注意:结果应符合实际意义
答:水渠应挖 1 m 宽.
我们利用“图形经过平移,它的面积大小不会改变”的性质,把纵、横两条水渠移动一下,使列方程更容易些(目的是求出水渠的宽,至于实际施工,仍可按原图的位置修路).
方法点拨
例6 一组学生组织春游,预计共需费用 120 元. 后来又有 2 人参加进来,费用不变,这样每人可少分摊 3 元. 问原来这组学生的人数是多少
分析:设原来这组学生的人数是 x,则可把题中信息整理成下表:
总费用/元 人数 每人费用/元
原来
现在
解:设原来这组学生的人数是 x,由题意得
两边同乘 x(x + 2),整理,得
x2 + 2x - 80 = 0.
解这个方程,得
x1 = -10,x2 = 8.
检验:x1 = -10,x2 = 8 都是原方程的根,
但 x = -10 不符合题意,所以取 x = 8.
答:原来这组学生是 8 人.
解分式方程应用题时,所得根不仅要检验是否为增根,还要考虑它是否符合题意.
方法点拨
随堂演练
1. 某厂今年一月份的总产量为 500 吨,三月份的总产量为 720 吨,平均每月的增长率是 x,则可列方程( )
A. 500(1 + 2x) = 720 B. 500(1 + x)2 = 720
C. 500(1 + x2) = 720 D. 720(1 + x)2 = 500
2. 某校去年对实验器材的投资为 2 万元,预计今明两年的投资总额为 8 万元.若设该校今明两年在实验器材投资上的平均增长率是 x,则可列方程为
.
B
2(1 + x) + 2(1 + x)2 = 8
3. 在一幅长 80 cm,宽 50 cm 的长方形风景画的四周镶一条金色纸边,制成一幅长方形挂图,如图所示,如果要使整个挂图的面积是 5400 cm2,设金色纸边的宽为 x cm,那么 x 满足的方程是( )
A.x2 + 130x - 1400 = 0
B.x2 + 65x - 350 = 0
C.x2 - 130x - 1400 = 0
D.x2 - 65x - 350 = 0
80 cm
x
x
x
x
50 cm
B
4. 青山村种的水稻前年平均每公顷产 7200 千克,今年平均每公顷产 8712 千克,求该村这两年水稻每公顷产量的年平均增长率.
解:设水稻每公顷产量的年平均增长率为 x.
根据题意,得 7200(1+x)2 = 8712.
解得 x1 = 0.1 = 10%,x2= -1.1(不符合题意,舍去).
答:水稻每公顷产量的年平均增长率为 10%.
5. 如图,在宽 20 米,长 32 米的长方形地面上修筑同样宽的道路 (图中阴影部分),余下的部分种上草坪. 要使草坪的面积为 540 平方米,求道路的宽.
解:设道路宽为 x 米,由平移得到下图,则依题意可列方程为
(20 - x)(32 - x) = 540.
解得 x1 = 50 (舍去),x2 = 2.
答:道路的宽为 2 米.
整理得 x2 - 52x + 100 = 0,
课堂小结
一元二次方程的应用
增长率
a(1 + x)2 = b,其中 a 为增长前的量,x 为增长率,2 为增长次数,b 为增长后的量
降低率
a(1 - x)2 = b,其中 a 为降低前的量,x 为降低率,2 为降低次数,b 为降低后的量. 注意 1 与 x 位置不可调换
平均变化率问题
几何图形
其他类型问题
常见几何图形面积是等量关系
第17章 一元二次方程
17.5 一元二次方程的应用
学习目标
1.能够利用一元二次方程解决有关实际问题,并能根据具体问题的实际意义,检验结果的合理性。(重点、难点)
2.认识方程模型的重要性,寻找实际问题中的相等关系。(难点)
3.在问题解决中,经历一定的合作交流活动,进一步发展学生合作交流的意识和能力。
知识讲解
知识点1 平均变化率问题与一元二次方程
填空:
1. 前年生产 1 吨甲种药品的成本是 5000 元,随着生产技术的进步,去年生产 1 吨甲种药品的成本是 4650 元,则下降率是 . 如果保持这个下降率,那么现在生产 1 吨甲种药品的成本是 元.
7%
4324.5
下降率 =
下降前的量 - 下降后的量
下降前的量
探究归纳
2. 前年生产 1 吨甲种药品的成本是 5000 元,随着生产技术的进步,设下降率是 x,则去年生产 1 吨甲种药品的成本是 元,如果保持这个下降率,那么现在生产 1 吨甲种药品的成本是 元.
下降率x
第一次下降前的量
5000(1 - x)
第一次下降后的量
5000
下降率x
第二次下降后的量
第二次下降前的量
5000(1 - x)(1 - x)
5000(1 - x)2
5000(1 - x)
5000(1 - x)2
例1 前年生产 1 吨甲种药品的成本是 5000 元,随着生产技术的进步,现在生产 1 吨甲种药品的成本是 4050 元,试求甲种药品成本的年平均下降率.
解:设甲种药品的年平均下降率为 x. 根据题意,列方程,得
5 000 (1 - x)2 = 4050,
解方程,得
x1 = 0.1,x2 = 1.9.
根据问题的实际意义,取 x = 0.1,
即甲种药品成本的年平均下降率为10%.
下降率不可为负,且不大于1.
注意
例题解读
例2 某公司去年的各项经营中,一月份的营业额为 200 万元,一月、二月、三月的营业额共 950 万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为 x.根据题意,得
答:这个增长率为 50%.
200 + 200(1 + x) + 200(1 + x)2 = 950.
整理方程,得 4x2 + 12x - 7 = 0.
解得 x1 = -3.5 (舍去),x2 = 0.5.
增长率不可为负,但可以超过 1.
注意
方法归纳
建立一元二次方程模型
实际问题
分析数量关系
设出未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
知识点2 几何图形与一元二次方程
例3 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的长方形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到 0.1 cm)?
27cm
21cm
分析:这本书的长宽之比为 : ,正中央的长方形的长宽之比为 : ,上下边衬与左右
边衬的宽度之比 : .
9
9
解析:设中央长方形的长和宽分别为 9a 和 7a,由此得到上下边衬宽度之比为
9
7
7
7
27cm
21cm
解1:设上下边衬的宽为 9x cm,左右边衬的宽为 7x cm. 依题意得
解得
故上下边衬的宽为
故左右边衬的宽为
方程的哪个根合乎实际意义
为什么
试一试:如果换一种设未知数的方法,是否可以更简单地解决上面的问题?
27cm
21cm
解2:设正中央的长方形的两边别为 9x cm,7x cm. 依题意得
解得
故上下边衬的宽度为
左右边衬的宽度为
27cm
21cm
在几何图形的面积问题中,面积公式往往就是建立等量关系的关键. 如果图形不规则,应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程.
方法点拨
例4 如图,在 Rt△ABC 中,∠C = 90°,AC = 6 cm,BC = 8 cm. 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s 的速度移动;同时点 Q 沿 CB 边从点 C 向终点 B 以 2 cm/s 的速度移动,且当其中一点到达终点时,另一点也随之停止移动. 问点 P,Q 出发几秒后可使 △PCQ 的面积为 9 cm ?
根据题意得 AP = x cm,PC = (6 - x) cm,CQ = 2x cm.
解:设点 P,Q 出发 x s 后 △PCQ 的面积为 9 cm .
整理,得
解得 x1 = x2 = 3.
答:点 P,Q 出发 3 s 后可使△PCQ的面积为 9 cm .
则有
例5 如图,在一块长为 92 m,宽为 60 m 的长方形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为 885 m2 的 6 个长方形小块.水渠应挖多宽?
解:设水渠宽为 x m,将所有耕地拼在一起,变成一个新的长方形,则其长为 (92 - 2x) m,宽为 (60 - x) m. 则有
(92 - 2x)(60 - x) = 6×885.
解得 x1 = 105(舍去),x2 = 1.
注意:结果应符合实际意义
答:水渠应挖 1 m 宽.
我们利用“图形经过平移,它的面积大小不会改变”的性质,把纵、横两条水渠移动一下,使列方程更容易些(目的是求出水渠的宽,至于实际施工,仍可按原图的位置修路).
方法点拨
例6 一组学生组织春游,预计共需费用 120 元. 后来又有 2 人参加进来,费用不变,这样每人可少分摊 3 元. 问原来这组学生的人数是多少
分析:设原来这组学生的人数是 x,则可把题中信息整理成下表:
总费用/元 人数 每人费用/元
原来
现在
解:设原来这组学生的人数是 x,由题意得
两边同乘 x(x + 2),整理,得
x2 + 2x - 80 = 0.
解这个方程,得
x1 = -10,x2 = 8.
检验:x1 = -10,x2 = 8 都是原方程的根,
但 x = -10 不符合题意,所以取 x = 8.
答:原来这组学生是 8 人.
解分式方程应用题时,所得根不仅要检验是否为增根,还要考虑它是否符合题意.
方法点拨
随堂演练
1. 某厂今年一月份的总产量为 500 吨,三月份的总产量为 720 吨,平均每月的增长率是 x,则可列方程( )
A. 500(1 + 2x) = 720 B. 500(1 + x)2 = 720
C. 500(1 + x2) = 720 D. 720(1 + x)2 = 500
2. 某校去年对实验器材的投资为 2 万元,预计今明两年的投资总额为 8 万元.若设该校今明两年在实验器材投资上的平均增长率是 x,则可列方程为
.
B
2(1 + x) + 2(1 + x)2 = 8
3. 在一幅长 80 cm,宽 50 cm 的长方形风景画的四周镶一条金色纸边,制成一幅长方形挂图,如图所示,如果要使整个挂图的面积是 5400 cm2,设金色纸边的宽为 x cm,那么 x 满足的方程是( )
A.x2 + 130x - 1400 = 0
B.x2 + 65x - 350 = 0
C.x2 - 130x - 1400 = 0
D.x2 - 65x - 350 = 0
80 cm
x
x
x
x
50 cm
B
4. 青山村种的水稻前年平均每公顷产 7200 千克,今年平均每公顷产 8712 千克,求该村这两年水稻每公顷产量的年平均增长率.
解:设水稻每公顷产量的年平均增长率为 x.
根据题意,得 7200(1+x)2 = 8712.
解得 x1 = 0.1 = 10%,x2= -1.1(不符合题意,舍去).
答:水稻每公顷产量的年平均增长率为 10%.
5. 如图,在宽 20 米,长 32 米的长方形地面上修筑同样宽的道路 (图中阴影部分),余下的部分种上草坪. 要使草坪的面积为 540 平方米,求道路的宽.
解:设道路宽为 x 米,由平移得到下图,则依题意可列方程为
(20 - x)(32 - x) = 540.
解得 x1 = 50 (舍去),x2 = 2.
答:道路的宽为 2 米.
整理得 x2 - 52x + 100 = 0,
课堂小结
一元二次方程的应用
增长率
a(1 + x)2 = b,其中 a 为增长前的量,x 为增长率,2 为增长次数,b 为增长后的量
降低率
a(1 - x)2 = b,其中 a 为降低前的量,x 为降低率,2 为降低次数,b 为降低后的量. 注意 1 与 x 位置不可调换
平均变化率问题
几何图形
其他类型问题
常见几何图形面积是等量关系
