18.1 第1课时 勾股定理 课件(共31张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 18.1 第1课时 勾股定理 课件(共31张PPT) 2023-2024学年数学沪科版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:26:13 | ||
图片预览







文档简介
(共31张PPT)
第18章 勾股定理
18.1 勾股定理
第1课时 勾股定理
学习目标
学习重难点
难点
重点
1.了解勾股定理的文化历史背景,会用面积法验证勾股定理.
2.掌握勾股定理的内容,能用勾股定理解决一些简单问题.
1.掌握勾股定理的内容.
2.会用勾股定理进行简单的计算.
勾股定理的验证.
情境导入
思考 你见过这个图案吗?它由哪些我们学过的基本图形组成?
国际数学家大会是最高水平的全球性数学科学学术
会议.2002年在北京召开了第24届国际数学家大会.如
图就是大会会徽的图案.
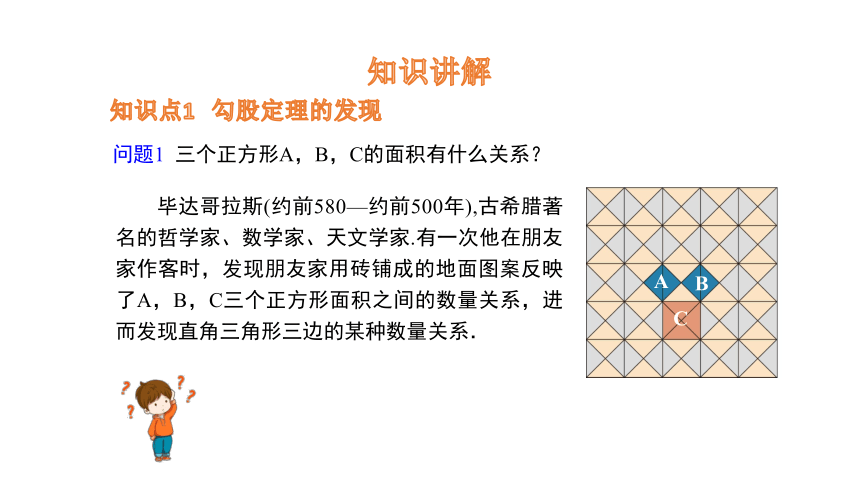
问题1 三个正方形A,B,C的面积有什么关系?
毕达哥拉斯(约前580—约前500年),古希腊著名的哲学家、数学家、天文学家.有一次他在朋友家作客时,发现朋友家用砖铺成的地面图案反映了A,B,C三个正方形面积之间的数量关系,进而发现直角三角形三边的某种数量关系.
A
B
C
知识讲解
知识点1 勾股定理的发现
问题1 三个正方形A,B,C的面积有什么关系?
发现
两个小正方形的面积之和等于大正方形的面积.
每块砖都是等腰直角三角形哦
SA+SB=SC
由这三个正方形A,B,C的边长构成的等腰直角三角形三条边长之间有怎样的特殊关系?
A
B
C
发现
等腰直角三角形两条直角边的平方和等于斜边的平方.
问题2 在网格中的一般的直角三角形,以它的三边为边长的三个正方形是否也有类似的面积关系?
A
B
C
A
C
B
正方形A的面积 正方形B的面积 正方形C
的面积
R
Q
P
9
16
?
如何求SC 的大小?有几种方案?
小方格的边长为1.
图1
A
Q
C
C
用“割”的方法
B
SC
图1
A
B
C
C
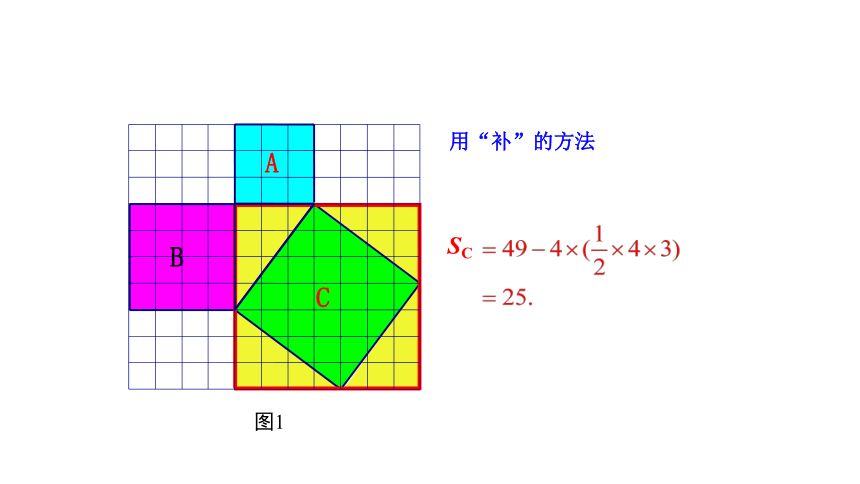
用“补”的方法
SC
图1
A
B
C
图2
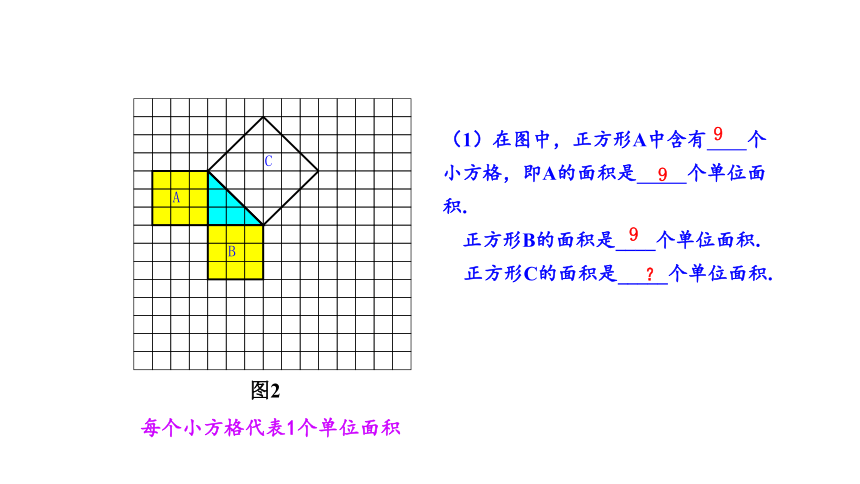
每个小方格代表1个单位面积
(1)在图中,正方形A中含有 个小方格,即A的面积是 个单位面积.
正方形B的面积是____个单位面积.
正方形C的面积是_____个单位面积.
9
9
9
?
A
B
C
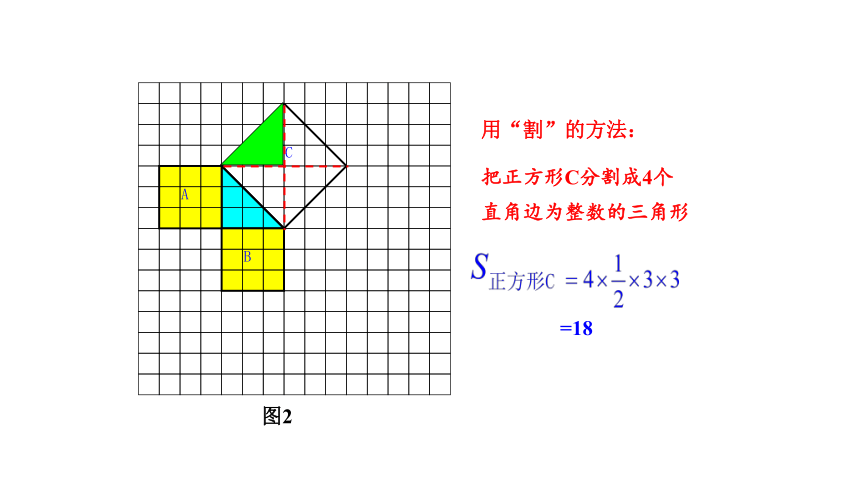
用“割”的方法:
把正方形C分割成4个直角边为整数的三角形
=18
图2
A
B
C
=18
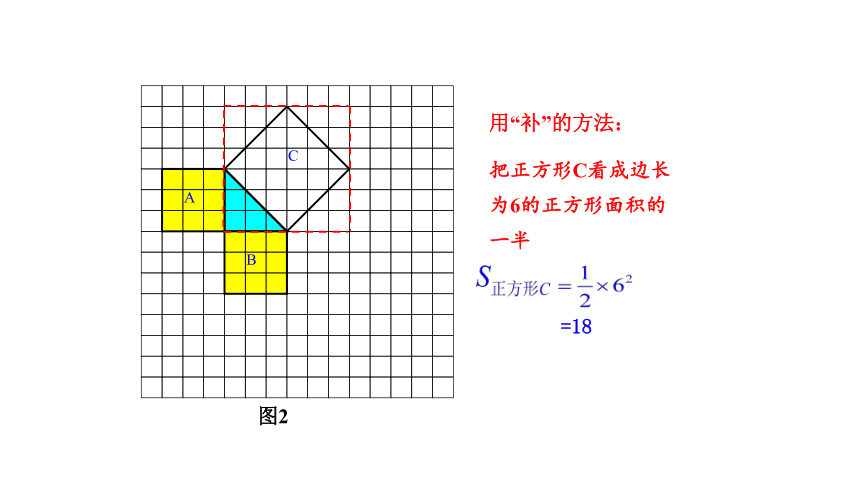
用“补”的方法:
把正方形C看成边长为6的正方形面积的一半
图2
A
B
C
图2
每个小方格代表1个单位面积
(1)在图中,正方形A中含有 个小方格,即A的面积是 个单位面积.
正方形B的面积是____个单位面积.
正方形C的面积是_____个单位面积.
9
9
9
18
正方形 A的面积
正方形B的面积
正方形C的面积
图1
图2
9
16
25
9
9
18
(1)填写下表:
(2)结论:SA+SB=SC
(3)归纳:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
A
B
C
图1
A
B
C
图2
问题3 通过前面的探究活动,猜一猜,直角三角形三边之间应该有什么关系?
命题1 直角三角形两条直角边的平方和,等于斜边的平方.
如果直角三角形的两直角边用a,b表示,斜边用c表示,那么勾股定理可表示为a2+b2=c2.
a
b
c
如何验证呢?
知识点2 勾股定理的证明
如图我国古代证明该命题的“赵爽弦图”.
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
四个全等的直角三角形(红色)可以如图围成一个大正方形,中空的部分是一个小正方形(黄色).
赵爽弦图
a
b
b
c
a
b
c
证法1 赵爽利用弦图证明
a
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.
证法2 毕达哥拉斯证法
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
例题讲解
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
解:
归纳 公式变形:
方程思想.
例2 求下列图中字母所表示的正方形的面积.
225
400
A
225
81
B
A=225+400=625
B=225-81=144
练习 求下列直角三角形中未知边的长度.
A
B
C
4
6
x
C
B
A
5
10
x
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理.为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票.
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中.
· 趣味拓展 ·
把一个正方形的面积分成若干个小正方形的面积的和,不断地分下去,就可以得到一棵美丽的勾股树.
勾股定理的演示
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
随堂演练
3.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a= ,∠A=60°,求b,c.
C
A
B
4.如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
解:在△ABC中,作AD⊥BC,垂足为点D,设BD=x,则CD=14-x.
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
所以152-x2=132-(14-x)2.解得x=9.所以BD=9.
在Rt△ABD中,
AD2=AB2-BD2=152-92=144,所以AD=12.
所以S△ABC= BC·AD= ×14×12=84.
课堂小结
内容
如果直角三角形的两直角边用a,b表示,斜边用c表示,那么勾股定理可表示为a2+b2=c2
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
勾股定理
第18章 勾股定理
18.1 勾股定理
第1课时 勾股定理
学习目标
学习重难点
难点
重点
1.了解勾股定理的文化历史背景,会用面积法验证勾股定理.
2.掌握勾股定理的内容,能用勾股定理解决一些简单问题.
1.掌握勾股定理的内容.
2.会用勾股定理进行简单的计算.
勾股定理的验证.
情境导入
思考 你见过这个图案吗?它由哪些我们学过的基本图形组成?
国际数学家大会是最高水平的全球性数学科学学术
会议.2002年在北京召开了第24届国际数学家大会.如
图就是大会会徽的图案.
问题1 三个正方形A,B,C的面积有什么关系?
毕达哥拉斯(约前580—约前500年),古希腊著名的哲学家、数学家、天文学家.有一次他在朋友家作客时,发现朋友家用砖铺成的地面图案反映了A,B,C三个正方形面积之间的数量关系,进而发现直角三角形三边的某种数量关系.
A
B
C
知识讲解
知识点1 勾股定理的发现
问题1 三个正方形A,B,C的面积有什么关系?
发现
两个小正方形的面积之和等于大正方形的面积.
每块砖都是等腰直角三角形哦
SA+SB=SC
由这三个正方形A,B,C的边长构成的等腰直角三角形三条边长之间有怎样的特殊关系?
A
B
C
发现
等腰直角三角形两条直角边的平方和等于斜边的平方.
问题2 在网格中的一般的直角三角形,以它的三边为边长的三个正方形是否也有类似的面积关系?
A
B
C
A
C
B
正方形A的面积 正方形B的面积 正方形C
的面积
R
Q
P
9
16
?
如何求SC 的大小?有几种方案?
小方格的边长为1.
图1
A
Q
C
C
用“割”的方法
B
SC
图1
A
B
C
C
用“补”的方法
SC
图1
A
B
C
图2
每个小方格代表1个单位面积
(1)在图中,正方形A中含有 个小方格,即A的面积是 个单位面积.
正方形B的面积是____个单位面积.
正方形C的面积是_____个单位面积.
9
9
9
?
A
B
C
用“割”的方法:
把正方形C分割成4个直角边为整数的三角形
=18
图2
A
B
C
=18
用“补”的方法:
把正方形C看成边长为6的正方形面积的一半
图2
A
B
C
图2
每个小方格代表1个单位面积
(1)在图中,正方形A中含有 个小方格,即A的面积是 个单位面积.
正方形B的面积是____个单位面积.
正方形C的面积是_____个单位面积.
9
9
9
18
正方形 A的面积
正方形B的面积
正方形C的面积
图1
图2
9
16
25
9
9
18
(1)填写下表:
(2)结论:SA+SB=SC
(3)归纳:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
A
B
C
图1
A
B
C
图2
问题3 通过前面的探究活动,猜一猜,直角三角形三边之间应该有什么关系?
命题1 直角三角形两条直角边的平方和,等于斜边的平方.
如果直角三角形的两直角边用a,b表示,斜边用c表示,那么勾股定理可表示为a2+b2=c2.
a
b
c
如何验证呢?
知识点2 勾股定理的证明
如图我国古代证明该命题的“赵爽弦图”.
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
四个全等的直角三角形(红色)可以如图围成一个大正方形,中空的部分是一个小正方形(黄色).
赵爽弦图
a
b
b
c
a
b
c
证法1 赵爽利用弦图证明
a
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.
证法2 毕达哥拉斯证法
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
例题讲解
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
解:
归纳 公式变形:
方程思想.
例2 求下列图中字母所表示的正方形的面积.
225
400
A
225
81
B
A=225+400=625
B=225-81=144
练习 求下列直角三角形中未知边的长度.
A
B
C
4
6
x
C
B
A
5
10
x
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理.为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票.
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中.
· 趣味拓展 ·
把一个正方形的面积分成若干个小正方形的面积的和,不断地分下去,就可以得到一棵美丽的勾股树.
勾股定理的演示
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
随堂演练
3.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a= ,∠A=60°,求b,c.
C
A
B
4.如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
解:在△ABC中,作AD⊥BC,垂足为点D,设BD=x,则CD=14-x.
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
所以152-x2=132-(14-x)2.解得x=9.所以BD=9.
在Rt△ABD中,
AD2=AB2-BD2=152-92=144,所以AD=12.
所以S△ABC= BC·AD= ×14×12=84.
课堂小结
内容
如果直角三角形的两直角边用a,b表示,斜边用c表示,那么勾股定理可表示为a2+b2=c2
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
勾股定理
