18.1 第2课时 勾股定理的应用 课件 (共27张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 18.1 第2课时 勾股定理的应用 课件 (共27张PPT) 2023-2024学年数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:26:42 | ||
图片预览




文档简介
(共27张PPT)
第18章 勾股定理
18.1 勾股定理
第2课时 勾股定理的应用
学习目标
学习重难点
难点
重点
1.能应用勾股定理计算直角三角形的边长.
2.能应用勾股定理解决简单的实际问题.
会运用勾股定理求线段长及解决简单的实际问题.
从实际问题中抽象出直角三角形,利用勾股定理建立已知边与未知边长度之间的联系.
情境导入
这节课我们就来学习用勾股定理解决实际问题.
知识讲解
知识点1 利用勾股定理解决实际问题
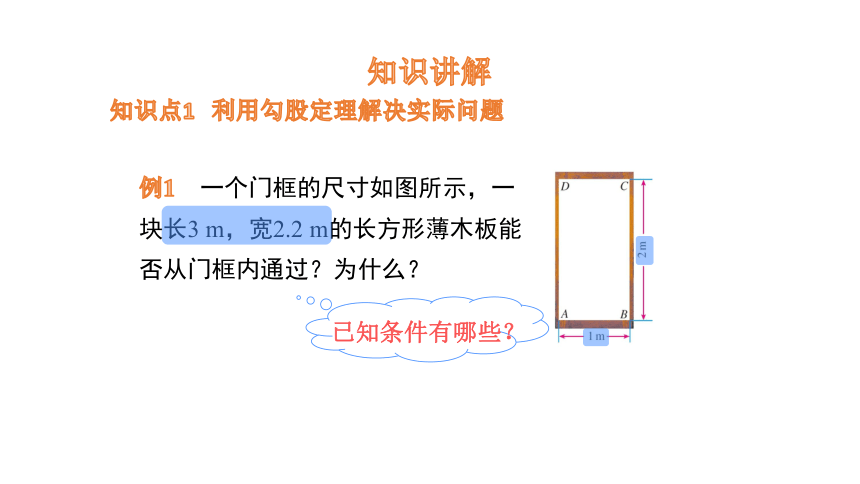
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
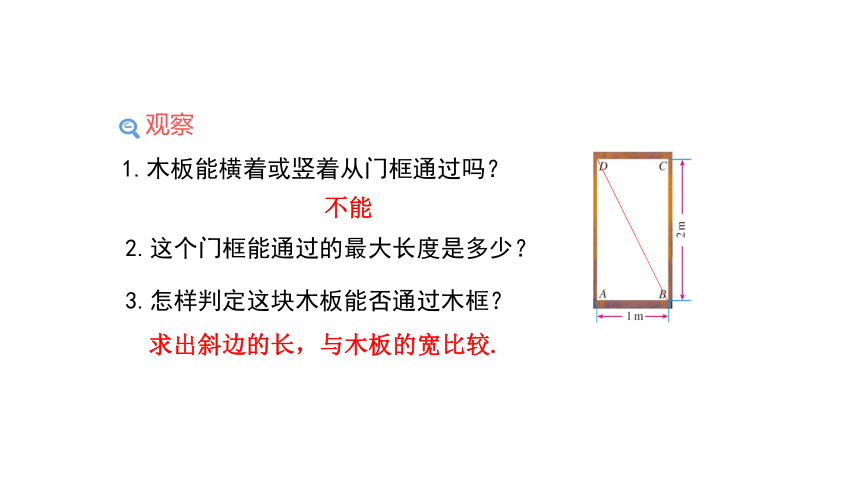
观察
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
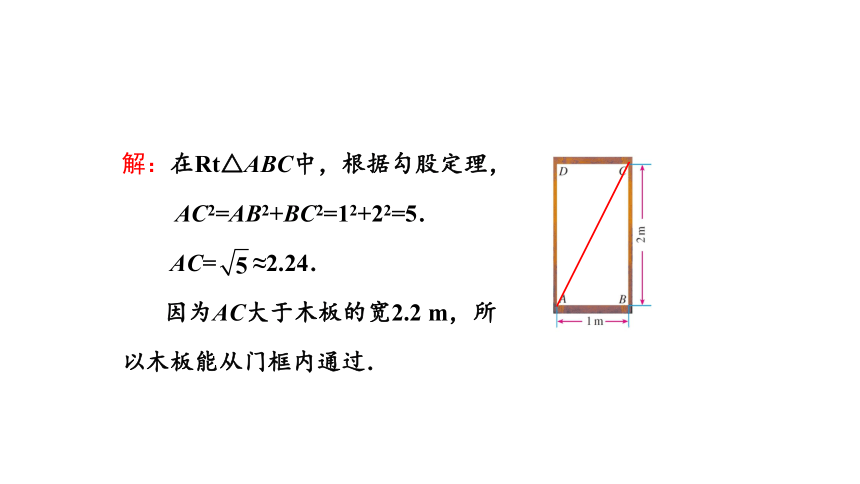
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
例2 如图,一架2.6 m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4 m. 如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗
解:在Rt△ABC中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5 m时,梯子底端并不是也外移0.5 m,而是外移约0.77 m.
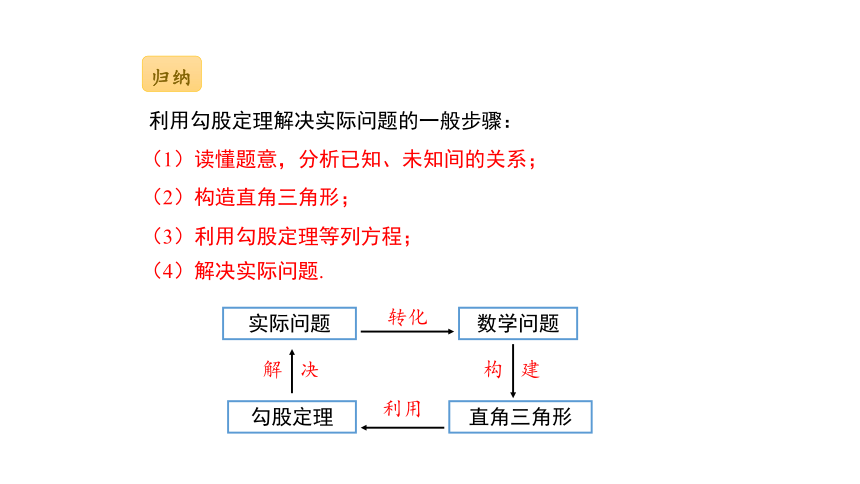
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
建
构
利用
决
解
归纳
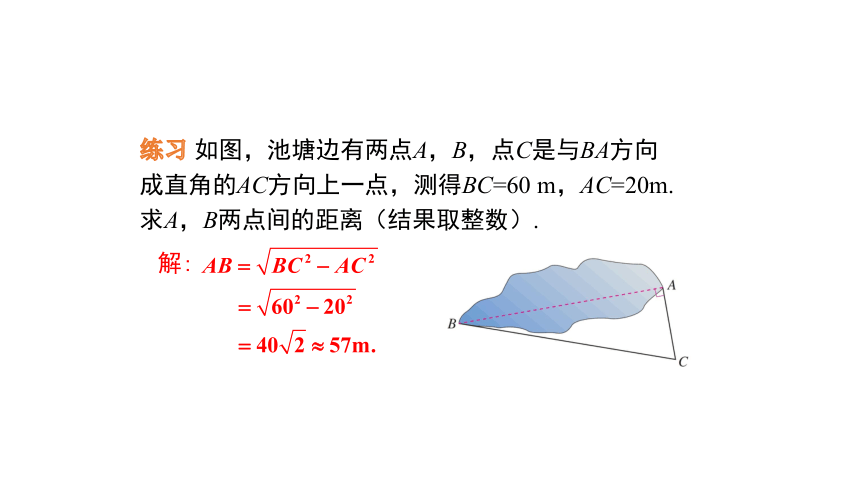
练习 如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
知识点2 两点之间的距离公式
那么
如果数轴上的点A1,A2
分别表示实数 x1,x2,
两点
A1,A2间的距离
记作│A1A2│,
│A1A2│=
│x2-x1│
对于平面上的两点A1,A2间的距离是否有类似的结论呢?
运用勾股定理,
就可以推出平面上两点之间的距离公式.
问题 1 如图,平面上两点A(3,0),B(0,4),如何计算A,B两点之间的距离│AB│?
解:
∵ A(3,0),B(0,4)
∴ OA=3,
∴ │AB│=
=5
OB=4
问题 2 如图,平面上两点A(1,2),B(5,5),如何计算这两点之间的距离│AB│?
解:
∵ A(1,2),B(5,5)
∴ AC=
∴ │AB│=
=5
5-1
=4
BC=
5-2
=3
两点之间的距离公式.
问题 3 一般地,设平面内任意两点A(x1,y1)和B(x2,y2),
如图,如何计算A,B两点之间的距离│AB│?
O
x
y
B(x2,y2)
A(x1,y1)
A''
A'
B'
B''
C
∵│CB│=
│A'B'│=
│x2-x1│
∵│CA│=
│B''A''│=
│y2-y1│
∴│AB│2=
│CB│2+│CA│2
=(x2-x1)2+(y2-y1)2
∴ │AB│=
解:
这就是平面直角坐标系中的
例3 如图,在平面直角坐标系中有两点 A(-3,5),B(1,2),求 A,B 两点间的距离.
A
2
1
-3
-2
-1
-1
2
3
1
4
5
y
O
x
3
B
C
解:如图,过点 A 作 x 轴的垂线,过点 B 作 x,y 轴的垂线,相交于点 C,连接 AB.
则 AC = 5 - 2 = 3,BC = 3 + 1 = 4.
在 Rt△ABC 中,由勾股定理得
∴ A,B 两点间的距离为 5.
知识点3 利用勾股定理求最短距离
C
B
A
问题 在 A 点的小狗,为了尽快吃到 B 点的香肠,它选择 A B 路线,而不选择 A C B 路线,难道小狗也懂数学?
AC+CB >AB(两点之间,线段最短)
思考 在立体图形中,怎么寻找最短路线呢?
A
B
蚂蚁从 A→B 的路线
问题:在一个圆柱形石凳上,小明在吃东西时留下了一点食物在 B 处,恰好在 A 处的一只蚂蚁捕捉到这一信息,于是它想沿侧面从 A 处爬向 B 处,问怎么走最近?最短路程怎么求?
B
A
将侧面展开后,根据“两点之间线段最短”可得最近路线.
若已知圆柱体高为 12 cm,底面半径为 3 cm,π 取 3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在 Rt△ABA′ 中,由勾股定理得
立体图形中求表面上两点间的最短距离,一般把立体图形展开成平面图形,根据“两点之间线段最短”确定最短路线,再根据勾股定理求最短路程.
归纳
例4 有一个圆柱形油罐,要以 A 点环绕油罐建梯子,正好建在 A 点的正上方点 B 处,问梯子最短需多少米(已知油罐的底面半径是 2 m,高 AB 是 5 m,π 取 3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则 AB' 为梯子的最短距离.
AA' = 2×3×2 = 12, A'B' = 5,根据勾股定理得
即梯子最短需 13 米.
数学思想:
立体图形
平面图形
转化
展开
随堂演练
1.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8米
B.10米
C.12米
D.14米
B
2.如图,一棵大树在一次强台风中距地面5 m处折断,倒下后树顶端着地点A距树底端B的距离为12 m,这棵大树在折断前的高度为( )
A.10 m
B.15 m
C.18 m
D.20 m
C
3. 已知点 (2,5),(-4,-3),则这两点的距离为____.
10
4.一个长方形零件(如图),根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
A
B
90
160
40
40
解: 过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
A
B
90
160
40
40
C
5.今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?
A
B
C
分析:
可设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52= ,
通过解方程可得.
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
C
7. 如图是一个三级台阶,它的每一级的长、宽和高分别等于 55 cm,10 cm 和 6 cm,A 和 B 是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想到 B 点去吃可口的食物. 这只蚂蚁爬行的最短路程是多少?
B
A
A
B
C
解:台阶的展开图如图,连接 AB.
在 Rt△ABC 中,根据勾股定理得
AB2 = BC2+AC2 = 552+482 = 5329 = 732.
∴ AB = 73 cm.
课堂小结
用勾股定理解决实际问题
要点:构造直角三角形
化非直角三角形为直角三角形
勾股定理的应用
用勾股定理解决两点之间的距离及最短路径问题
第18章 勾股定理
18.1 勾股定理
第2课时 勾股定理的应用
学习目标
学习重难点
难点
重点
1.能应用勾股定理计算直角三角形的边长.
2.能应用勾股定理解决简单的实际问题.
会运用勾股定理求线段长及解决简单的实际问题.
从实际问题中抽象出直角三角形,利用勾股定理建立已知边与未知边长度之间的联系.
情境导入
这节课我们就来学习用勾股定理解决实际问题.
知识讲解
知识点1 利用勾股定理解决实际问题
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
观察
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
例2 如图,一架2.6 m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4 m. 如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗
解:在Rt△ABC中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5 m时,梯子底端并不是也外移0.5 m,而是外移约0.77 m.
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
建
构
利用
决
解
归纳
练习 如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
知识点2 两点之间的距离公式
那么
如果数轴上的点A1,A2
分别表示实数 x1,x2,
两点
A1,A2间的距离
记作│A1A2│,
│A1A2│=
│x2-x1│
对于平面上的两点A1,A2间的距离是否有类似的结论呢?
运用勾股定理,
就可以推出平面上两点之间的距离公式.
问题 1 如图,平面上两点A(3,0),B(0,4),如何计算A,B两点之间的距离│AB│?
解:
∵ A(3,0),B(0,4)
∴ OA=3,
∴ │AB│=
=5
OB=4
问题 2 如图,平面上两点A(1,2),B(5,5),如何计算这两点之间的距离│AB│?
解:
∵ A(1,2),B(5,5)
∴ AC=
∴ │AB│=
=5
5-1
=4
BC=
5-2
=3
两点之间的距离公式.
问题 3 一般地,设平面内任意两点A(x1,y1)和B(x2,y2),
如图,如何计算A,B两点之间的距离│AB│?
O
x
y
B(x2,y2)
A(x1,y1)
A''
A'
B'
B''
C
∵│CB│=
│A'B'│=
│x2-x1│
∵│CA│=
│B''A''│=
│y2-y1│
∴│AB│2=
│CB│2+│CA│2
=(x2-x1)2+(y2-y1)2
∴ │AB│=
解:
这就是平面直角坐标系中的
例3 如图,在平面直角坐标系中有两点 A(-3,5),B(1,2),求 A,B 两点间的距离.
A
2
1
-3
-2
-1
-1
2
3
1
4
5
y
O
x
3
B
C
解:如图,过点 A 作 x 轴的垂线,过点 B 作 x,y 轴的垂线,相交于点 C,连接 AB.
则 AC = 5 - 2 = 3,BC = 3 + 1 = 4.
在 Rt△ABC 中,由勾股定理得
∴ A,B 两点间的距离为 5.
知识点3 利用勾股定理求最短距离
C
B
A
问题 在 A 点的小狗,为了尽快吃到 B 点的香肠,它选择 A B 路线,而不选择 A C B 路线,难道小狗也懂数学?
AC+CB >AB(两点之间,线段最短)
思考 在立体图形中,怎么寻找最短路线呢?
A
B
蚂蚁从 A→B 的路线
问题:在一个圆柱形石凳上,小明在吃东西时留下了一点食物在 B 处,恰好在 A 处的一只蚂蚁捕捉到这一信息,于是它想沿侧面从 A 处爬向 B 处,问怎么走最近?最短路程怎么求?
B
A
将侧面展开后,根据“两点之间线段最短”可得最近路线.
若已知圆柱体高为 12 cm,底面半径为 3 cm,π 取 3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在 Rt△ABA′ 中,由勾股定理得
立体图形中求表面上两点间的最短距离,一般把立体图形展开成平面图形,根据“两点之间线段最短”确定最短路线,再根据勾股定理求最短路程.
归纳
例4 有一个圆柱形油罐,要以 A 点环绕油罐建梯子,正好建在 A 点的正上方点 B 处,问梯子最短需多少米(已知油罐的底面半径是 2 m,高 AB 是 5 m,π 取 3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则 AB' 为梯子的最短距离.
AA' = 2×3×2 = 12, A'B' = 5,根据勾股定理得
即梯子最短需 13 米.
数学思想:
立体图形
平面图形
转化
展开
随堂演练
1.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8米
B.10米
C.12米
D.14米
B
2.如图,一棵大树在一次强台风中距地面5 m处折断,倒下后树顶端着地点A距树底端B的距离为12 m,这棵大树在折断前的高度为( )
A.10 m
B.15 m
C.18 m
D.20 m
C
3. 已知点 (2,5),(-4,-3),则这两点的距离为____.
10
4.一个长方形零件(如图),根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
A
B
90
160
40
40
解: 过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
A
B
90
160
40
40
C
5.今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?
A
B
C
分析:
可设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52= ,
通过解方程可得.
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
C
7. 如图是一个三级台阶,它的每一级的长、宽和高分别等于 55 cm,10 cm 和 6 cm,A 和 B 是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想到 B 点去吃可口的食物. 这只蚂蚁爬行的最短路程是多少?
B
A
A
B
C
解:台阶的展开图如图,连接 AB.
在 Rt△ABC 中,根据勾股定理得
AB2 = BC2+AC2 = 552+482 = 5329 = 732.
∴ AB = 73 cm.
课堂小结
用勾股定理解决实际问题
要点:构造直角三角形
化非直角三角形为直角三角形
勾股定理的应用
用勾股定理解决两点之间的距离及最短路径问题
