19.2 第3课时平行四边形的判定 课件 (共25张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 19.2 第3课时平行四边形的判定 课件 (共25张PPT) 2023-2024学年数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 881.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:25:45 | ||
图片预览







文档简介
(共25张PPT)
第19章 四边形
19.2 平行四边形
第3课时 平行四边形的判定
学习目标
学习重难点
难点
重点
1.通过对平行四边形判别条件的探索,得出判定平行四边形的方法.
2.能证明平行四边形的判定定理,并能用平行四边形的判定定理解决实际问题.
掌握平行四边形的判定定理,能根据已知条件选择合适的判定定理判定一个四边形是平行四边形.
能够灵活运用平行四边形的性质定理和判定定理进行简单的推理证明.
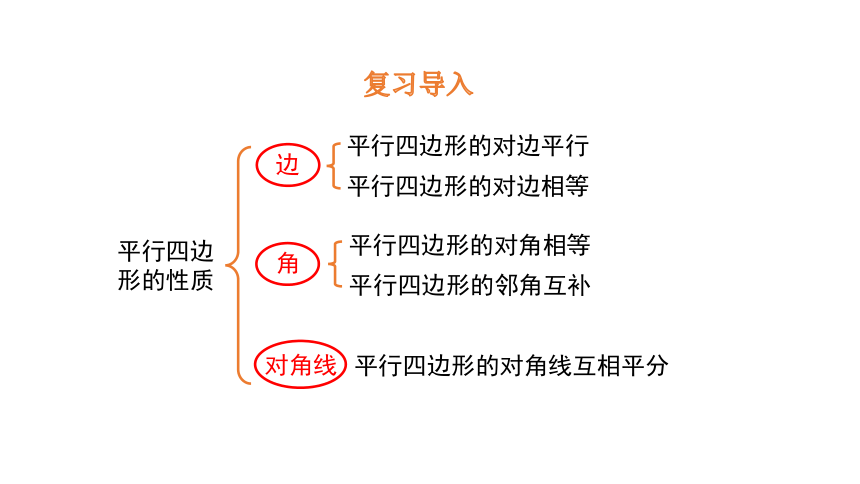
复习导入
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对角线
学行四边形之后,小明回家用细木棒钉制了一个平行四边形. 第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢
大家都困惑了……
知识讲解
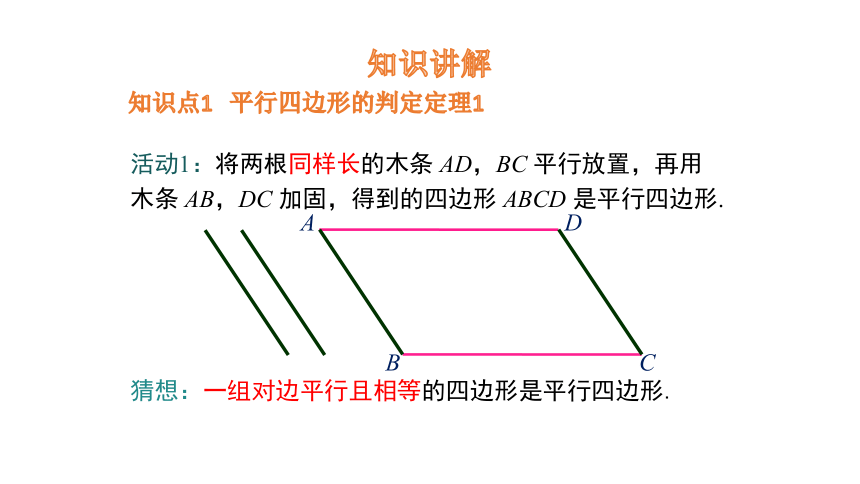
知识点1 平行四边形的判定定理1
活动1:将两根同样长的木条 AD,BC 平行放置,再用木条 AB,DC 加固,得到的四边形 ABCD 是平行四边形.
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
连接 AC.
∵ AB∥CD,∴∠1 =∠2.
又 AB = CD,AC = CA,
∴ △ABC≌△CDA (SAS).
∴ ∠3 = ∠4. ∴ AD∥BC.
∴ 四边形 ABCD 是平行四边形.
B
A
D
C
已知:如图,在四边形 ABCD 中,AB∥CD,AB = CD.
求证:四边形 ABCD 是平行四边形.
证明:
1
2
3
4
证一证
一组对边平行且相等的四边形是平行四边形.
∵ AB = CD,
AB∥CD,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理 1
B
D
C
A
总结归纳
例1 如图,在平行四边形 ABCD 中,已知 AE,CF 分别是∠DAB,∠BCD 的平分线,求证:四边形 AFCE 是平行四边形.
证明:在 □ ABCD 中,∠B =∠D,AB = CD,∠DAB =∠BCD.
∵ AE,CF 分别是∠DAB,∠BCD 的平分线,
∴∠BAE =∠DCF = ∠DAB = ∠BCD.
∴△ABE≌△CDF (ASA).
∴ BE = DF.则由 BC = DA 可得 CE = AF. 又∵ CE∥AF,
∴ 四边形 AFCE 是平行四边形. (一组对边平行且相等的四边形是平行四边形)
知识点2 平行四边形的判定定理2
活动2:用两根长 30 cm 的木条和两根长 20 cm 的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
20 cm
30 cm
猜测:两组对边分别相等的四边形是平行四边形.
已知:四边形 ABCD 中,AB = CD,AD = CB.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
连接 BD.
在 △ABD 和 △CDB 中,
AB = CD,
BD = DB,
AD = CB,
∴△ABD≌△CDB (SSS).
∴∠1 =∠3,∠2 =∠4.
∴ AB∥CD,AD∥CB.
∴ 四边形 ABCD 是平行四边形.
证明:
1
4
2
3
证一证
两组对边分别相等的四边形是平行四边形.
∵ AB = CD,
AD = BC,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理 2
总结归纳
B
D
C
A
例2 如图,在平行四边形 ABCD 中,E,F 分别是边 BC 和 AD 上的两点,且 AF = CE.
求证:四边形 AECF 为平行四边形.
B
A
C
D
F
E
证明:易得 △ABE≌△CDF (SAS).
∴ AE = CF.
又∵ AF = CE,
∴ 四边形 ABCD 是平行四边形.(两组对边分别相等的四边形是平行四边形)
知识点3 平行四边形的判定定理3
活动3:将两根木条 AC,BD 的中点重叠,并用钉子固定,再用一根橡皮筋绕端点 A,B,C,D 围成一个四边形.想一想,△AOB 与 △COD 全等吗?四边形 ABCD 的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
已知:四边形 ABCD 中,OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
证明:
在△AOB 和 △COD 中,
OA = OC,(已知)
OB = OD,(已知)
∠AOB =∠COD,(对顶角相等)
∴ △AOB≌△COD (SAS).
∴ AB = CD,∠ABO =∠CDO.
∴ AB∥CD.
∴ 四边形 ABCD 是平行四边形.
A
C
B
O
D
证一证
对角线互相平分的四边形是平行四边形.
∵ OA = OC,
OB = OD,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理 3
总结归纳
A
C
B
O
D
例3 已知:E、F 是平行四边形 ABCD 对角线 AC 上的两点,并且 AE = CF.
求证:四边形 BFDE 是平行四边形.
O
B
A
C
E
F
D
证明:连接 BD.
在平行四边形 ABCD 中,OA = OC,OB = OD.
∵ AE = CF,
∴ OA - AE = OC - CF,
即 EO = FO.
又 ∵ BO = DO,
∴ 四边形 BFDE 是平行四边形.
(对角线互相平分的四边形是平行四边形)
思考:我们可以从对角的关系出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
已知:四边形 ABCD 中,∠A =∠C,∠B =∠D,
求证:四边形 ABCD 是平行四边形.
A
B
C
D
且∠A =∠C,∠B =∠D,
∵∠A +∠C +∠B +∠D = 360°,
∴ 2∠A + 2∠B = 360°,
即∠A +∠B = 180°.
∴ AD∥BC.
∴ 四边形ABCD 是平行四边形.
同理得 AB∥CD,
证明:
判定方法:
两组对角分别相等的四边形是平行四边形
本教材未给出
随堂演练
1. 能判定四边形 ABCD 是平行四边形的条件:∠A :∠B : ∠C :∠D 的值为( )
A. 1 : 2 : 3 : 4
B. 1 : 4 : 2 : 3
C. 1 : 2 : 2 : 1
D. 3 : 2 : 3 : 2
D
2. 如图所示,△ABC 是等边三角形,P 是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若 △ABC 的周长为 24,则 PD + PE + PF = .
A
F
B
D
C
E
P
8
3. 已知 AD∥BC ,要使这个四边形 ABCD 为平行四边形,需要增加条件__________
________.
AD = BC 或
AB∥CD
4.在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
A
B
D
C
(如图,反例)
4.
如图,在四边形ABCD中,AB∥CD,要使四形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C. ∠A=∠C
D.BC∥AD
B
5.如图,在 ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,则 图中平行四边形共有( )
A.2个 B.3个 C.4个 D.6个
C
6.请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
(3)
(2)
A
B
C
D
120°
60°
5㎝
5㎝
B
A
D
C
4.8㎝
4.8㎝
(1)
7.6㎝
7.6㎝
(1)是.因为一组对边平行且相等的四边形是平行四边形
(2)是.因为两组对边分别平行的四边形是平行四边形
(3)是.因为两组对边分别相等的四边形是平行四边形
7. 已知:如图,在四边形 ABCD 中,AB∥CD,E 是 BC 的中点,直线 AE 交 DC 的延长线于点 F.试判断四边形 ABFC 的形状,并证明你的结论.
解:四边形 ABFC 是平行四边形. 证明如下:
∵ AB∥CD,∴∠BAE =∠CFE.
∵ E 是 BC 的中点,∴ BE = CE.
又∵∠AEB =∠FEC,
∴ △ABE≌△FCE(AAS).
∴ AE = FE.
∴ 四边形 ABFC 是平行四边形.
课堂小结
从边考虑
两组对边分别平行(定义法)
两组对边分别相等(判定定理2)
一组对边平行且相等(判定定理1)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等(定义拓展)
对角线互相平分(判定定理3)
第19章 四边形
19.2 平行四边形
第3课时 平行四边形的判定
学习目标
学习重难点
难点
重点
1.通过对平行四边形判别条件的探索,得出判定平行四边形的方法.
2.能证明平行四边形的判定定理,并能用平行四边形的判定定理解决实际问题.
掌握平行四边形的判定定理,能根据已知条件选择合适的判定定理判定一个四边形是平行四边形.
能够灵活运用平行四边形的性质定理和判定定理进行简单的推理证明.
复习导入
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对角线
学行四边形之后,小明回家用细木棒钉制了一个平行四边形. 第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢
大家都困惑了……
知识讲解
知识点1 平行四边形的判定定理1
活动1:将两根同样长的木条 AD,BC 平行放置,再用木条 AB,DC 加固,得到的四边形 ABCD 是平行四边形.
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
连接 AC.
∵ AB∥CD,∴∠1 =∠2.
又 AB = CD,AC = CA,
∴ △ABC≌△CDA (SAS).
∴ ∠3 = ∠4. ∴ AD∥BC.
∴ 四边形 ABCD 是平行四边形.
B
A
D
C
已知:如图,在四边形 ABCD 中,AB∥CD,AB = CD.
求证:四边形 ABCD 是平行四边形.
证明:
1
2
3
4
证一证
一组对边平行且相等的四边形是平行四边形.
∵ AB = CD,
AB∥CD,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理 1
B
D
C
A
总结归纳
例1 如图,在平行四边形 ABCD 中,已知 AE,CF 分别是∠DAB,∠BCD 的平分线,求证:四边形 AFCE 是平行四边形.
证明:在 □ ABCD 中,∠B =∠D,AB = CD,∠DAB =∠BCD.
∵ AE,CF 分别是∠DAB,∠BCD 的平分线,
∴∠BAE =∠DCF = ∠DAB = ∠BCD.
∴△ABE≌△CDF (ASA).
∴ BE = DF.则由 BC = DA 可得 CE = AF. 又∵ CE∥AF,
∴ 四边形 AFCE 是平行四边形. (一组对边平行且相等的四边形是平行四边形)
知识点2 平行四边形的判定定理2
活动2:用两根长 30 cm 的木条和两根长 20 cm 的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
20 cm
30 cm
猜测:两组对边分别相等的四边形是平行四边形.
已知:四边形 ABCD 中,AB = CD,AD = CB.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
连接 BD.
在 △ABD 和 △CDB 中,
AB = CD,
BD = DB,
AD = CB,
∴△ABD≌△CDB (SSS).
∴∠1 =∠3,∠2 =∠4.
∴ AB∥CD,AD∥CB.
∴ 四边形 ABCD 是平行四边形.
证明:
1
4
2
3
证一证
两组对边分别相等的四边形是平行四边形.
∵ AB = CD,
AD = BC,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理 2
总结归纳
B
D
C
A
例2 如图,在平行四边形 ABCD 中,E,F 分别是边 BC 和 AD 上的两点,且 AF = CE.
求证:四边形 AECF 为平行四边形.
B
A
C
D
F
E
证明:易得 △ABE≌△CDF (SAS).
∴ AE = CF.
又∵ AF = CE,
∴ 四边形 ABCD 是平行四边形.(两组对边分别相等的四边形是平行四边形)
知识点3 平行四边形的判定定理3
活动3:将两根木条 AC,BD 的中点重叠,并用钉子固定,再用一根橡皮筋绕端点 A,B,C,D 围成一个四边形.想一想,△AOB 与 △COD 全等吗?四边形 ABCD 的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
已知:四边形 ABCD 中,OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
证明:
在△AOB 和 △COD 中,
OA = OC,(已知)
OB = OD,(已知)
∠AOB =∠COD,(对顶角相等)
∴ △AOB≌△COD (SAS).
∴ AB = CD,∠ABO =∠CDO.
∴ AB∥CD.
∴ 四边形 ABCD 是平行四边形.
A
C
B
O
D
证一证
对角线互相平分的四边形是平行四边形.
∵ OA = OC,
OB = OD,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理 3
总结归纳
A
C
B
O
D
例3 已知:E、F 是平行四边形 ABCD 对角线 AC 上的两点,并且 AE = CF.
求证:四边形 BFDE 是平行四边形.
O
B
A
C
E
F
D
证明:连接 BD.
在平行四边形 ABCD 中,OA = OC,OB = OD.
∵ AE = CF,
∴ OA - AE = OC - CF,
即 EO = FO.
又 ∵ BO = DO,
∴ 四边形 BFDE 是平行四边形.
(对角线互相平分的四边形是平行四边形)
思考:我们可以从对角的关系出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
已知:四边形 ABCD 中,∠A =∠C,∠B =∠D,
求证:四边形 ABCD 是平行四边形.
A
B
C
D
且∠A =∠C,∠B =∠D,
∵∠A +∠C +∠B +∠D = 360°,
∴ 2∠A + 2∠B = 360°,
即∠A +∠B = 180°.
∴ AD∥BC.
∴ 四边形ABCD 是平行四边形.
同理得 AB∥CD,
证明:
判定方法:
两组对角分别相等的四边形是平行四边形
本教材未给出
随堂演练
1. 能判定四边形 ABCD 是平行四边形的条件:∠A :∠B : ∠C :∠D 的值为( )
A. 1 : 2 : 3 : 4
B. 1 : 4 : 2 : 3
C. 1 : 2 : 2 : 1
D. 3 : 2 : 3 : 2
D
2. 如图所示,△ABC 是等边三角形,P 是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若 △ABC 的周长为 24,则 PD + PE + PF = .
A
F
B
D
C
E
P
8
3. 已知 AD∥BC ,要使这个四边形 ABCD 为平行四边形,需要增加条件__________
________.
AD = BC 或
AB∥CD
4.在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
A
B
D
C
(如图,反例)
4.
如图,在四边形ABCD中,AB∥CD,要使四形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C. ∠A=∠C
D.BC∥AD
B
5.如图,在 ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,则 图中平行四边形共有( )
A.2个 B.3个 C.4个 D.6个
C
6.请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
(3)
(2)
A
B
C
D
120°
60°
5㎝
5㎝
B
A
D
C
4.8㎝
4.8㎝
(1)
7.6㎝
7.6㎝
(1)是.因为一组对边平行且相等的四边形是平行四边形
(2)是.因为两组对边分别平行的四边形是平行四边形
(3)是.因为两组对边分别相等的四边形是平行四边形
7. 已知:如图,在四边形 ABCD 中,AB∥CD,E 是 BC 的中点,直线 AE 交 DC 的延长线于点 F.试判断四边形 ABFC 的形状,并证明你的结论.
解:四边形 ABFC 是平行四边形. 证明如下:
∵ AB∥CD,∴∠BAE =∠CFE.
∵ E 是 BC 的中点,∴ BE = CE.
又∵∠AEB =∠FEC,
∴ △ABE≌△FCE(AAS).
∴ AE = FE.
∴ 四边形 ABFC 是平行四边形.
课堂小结
从边考虑
两组对边分别平行(定义法)
两组对边分别相等(判定定理2)
一组对边平行且相等(判定定理1)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等(定义拓展)
对角线互相平分(判定定理3)
