19.3.1 第2课时矩形的判定 课件 (共23张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 19.3.1 第2课时矩形的判定 课件 (共23张PPT) 2023-2024学年数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:30:14 | ||
图片预览








文档简介
(共23张PPT)
第19章 四边形
19.3 矩形、菱形、正方形
19.3.1 矩形
第2课时 矩形的判定
学习目标
1.经历矩形判定定理的探索过程,理解并掌握矩形的判定方
法.
2.能应用矩形判定解决简单的证明题和计算题.
学习重难点
难点
重点
理解并掌握矩形的判定方法.
能应用矩形判定解决简单的证明题和计算题.
复习导入
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
思考 工人师傅在做矩形门窗或零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
知识讲解
知识点1 对角线相等的平行四边形是矩形
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
问题1 除了定义以外,还有其他判定矩形的方法吗?
类似地,那我们研究矩形的性质的逆命题是否成立.
矩形是特殊的平行四边形.
问题2 上节课我们已经知道“矩形的对角线相等”,反过来,小明猜想对角线相等的四边形是矩形,你觉得对吗?
思考 你能证明这一猜想吗?
我猜想:对角线相等的四边形是矩形.
不对,等腰梯形的对角线也相等.
不对,矩形是特殊的平行四边形,所以它的对角线不仅相等且平分.
已知:如图,在□ABCD中,AC,DB 是它的两条对角线,且 AC = DB. 求证:□ABCD 是矩形.
证明:∵ AB = DC,BC = CB,AC = DB,
∴△ABC≌△DCB.
∴∠ABC =∠DCB.
∵ AB∥CD,
∴∠ABC +∠DCB = 180°.
∴∠ABC = 90°.
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
证一证
矩形的判定定理1:
对角线相等的平行四边形是矩形.
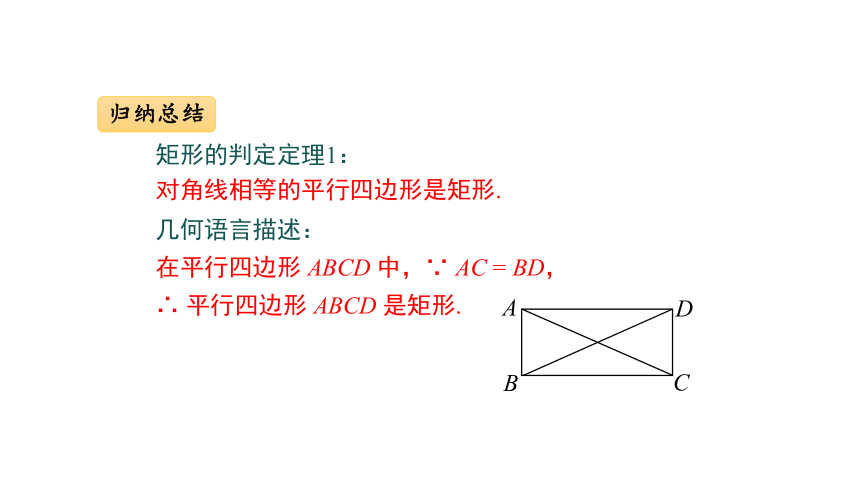
归纳总结
几何语言描述:
在平行四边形 ABCD 中,∵ AC = BD,
∴ 平行四边形 ABCD 是矩形.
A
D
C
B
思考 数学来源于生活,事实上工人师傅为了检验两组对边相等的四边形窗框是否成矩形,其中一种方法就是量一量这个四边形的两条对角线长度,如果对角线长相等,那么窗框一定是矩形,你
现在知道为什么了吗?
对角线相等的平行四边形是矩形.
例题解读
例1 如图,在 □ABCD 中,对角线 AC,BD 相交于点 O,且 OA = OD,∠OAD = 50°.求∠OAB 的度数.
A
B
C
D
O
解:∵ 四边形 ABCD 是平行四边形,
∴ OA = OC = AC,
OB = OD = BD.
又∵ OA = OD,
∴ AC = BD.
∴ 四边形 ABCD 是矩形.
∴∠BAD = 90°.
又∵∠OAD = 50°,
∴∠OAB = 40°.
例2 如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,E、F、G、H 分别是 AO、BO、CO、DO 上的一点,且 AE = BF = CG = DH. 求证:四边形 EFGH 是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵ 四边形 ABCD 是矩形,
∴ AC = BD(矩形的对角线相等),
AO = BO = CO = DO(矩形的对角线互相平分).
∵ AE = BF = CG = DH,
∴ OE = OF = OG = OH.
∴ 四边形 EFGH 是平行四边形,
且 EG = FH.
∴ 四边形 EFGH 是矩形.
知识点2 三个角是直角的四边形是矩形
问题1 上节课我们研究了矩形的四个角,知道它们都是直角,这个性质的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立.
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有两个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
已知:如图,在四边形 ABCD 中,∠A =∠B =∠C = 90°.
求证:四边形 ABCD 是矩形.
证明:∵∠A =∠B =∠C = 90°,
∴∠A +∠B = 180°,∠B +∠C = 180°.
∴ AD∥BC,AB∥CD.
∴ 四边形 ABCD 是平行四边形.
∴ 四边形 ABCD 是矩形.
A
B
C
D
证一证
矩形的判定定理2:
有三个角是直角的四边形是矩形.
归纳总结
几何语言描述:
在四边形 ABCD 中,∵∠A =∠B =∠C = 90°,
∴ 四边形 ABCD 是矩形.
A
B
C
D
思考 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板.为什么?
有三个角是直角的四边形是矩形.
例3 如图,□ ABCD 的四个内角的平分线分别相交于 E、F、G、H,求证:四边形 EFGH 为矩形.
证明:在□ ABCD 中,AD∥BC,
∴∠DAB +∠ABC = 180°.
∵ AE 与 BG 分别为∠DAB、
∠ABC 的平分线,
A
B
D
C
H
E
F
G
∴ 四边形 EFGH 为矩形.
同理可得∠FEH =∠EHG = 90°,
∴∠AFB = 90°.
∴∠GFE = 90°.
∴∠BAF +∠ABF = ∠DAB + ∠ABC = 90°.
例4 如图,在△ABC 中,AB=AC,AD⊥BC,垂足为 D,AN 是△ABC 的外角∠CAM 的平分线,CE⊥AN,垂足为 E,求证:四边形 ADCE 为矩形.
∴∠MAE=∠CAE= ∠CAM.
= (∠BAC+∠CAM )=90°.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵ AN 是△ABC 外角∠CAM 的平分线,
∴∠DAE=∠DAC+∠CAE
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°.
∴ 四边形 ADCE 为矩形.
C
1.如图,直线EF∥MN,PQ交EF,MN于A,C两点,AB,CB,CD,AD分别是∠EAC, ∠MCA, ∠ ACN,∠CAF的角平分线,则四边形ABCD是( )
D
E
F
M
N
Q
P
A
B
C
A.菱形 B.平行四边形 C.矩形 D.不能确定
随堂演练
2.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
D
3.下列命题是真命题的是( )
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形
D.对角线互相垂直的四边形是矩形
C
4. 如图,在△ABC中,AD 为 BC 边上的中线,延长 AD 至 E,使 DE = AD,连接 BE,CE.
(1)试判断四边形 ABEC 的形状;
(2)当△ABC 满足什么条件时,四边形 ABEC 是矩形?
解:(1)四边形 ABEC 是平行四边形.
(2)当△ABC 满足∠BAC=90°时,四边形 ABEC 是矩形.
A
B
C
E
D
5.已知:如图,在 □ ABCD 中,M 是 AD 边的中点,且MB = MC. 求证:四边形 ABCD 是矩形.
证明:在□ ABCD 中,AB = CD,
∵M 是 AD 边的中点,∴MA = MD,且 MB = MC,
即△ABM≌△DCM,∴∠A =∠D.
又∵∠A +∠D = 180°,
∴∠A =∠D = 90°,∴四边形ABCD是矩形.
A
B
D
C
M
课堂小结
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
第19章 四边形
19.3 矩形、菱形、正方形
19.3.1 矩形
第2课时 矩形的判定
学习目标
1.经历矩形判定定理的探索过程,理解并掌握矩形的判定方
法.
2.能应用矩形判定解决简单的证明题和计算题.
学习重难点
难点
重点
理解并掌握矩形的判定方法.
能应用矩形判定解决简单的证明题和计算题.
复习导入
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
思考 工人师傅在做矩形门窗或零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
知识讲解
知识点1 对角线相等的平行四边形是矩形
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
问题1 除了定义以外,还有其他判定矩形的方法吗?
类似地,那我们研究矩形的性质的逆命题是否成立.
矩形是特殊的平行四边形.
问题2 上节课我们已经知道“矩形的对角线相等”,反过来,小明猜想对角线相等的四边形是矩形,你觉得对吗?
思考 你能证明这一猜想吗?
我猜想:对角线相等的四边形是矩形.
不对,等腰梯形的对角线也相等.
不对,矩形是特殊的平行四边形,所以它的对角线不仅相等且平分.
已知:如图,在□ABCD中,AC,DB 是它的两条对角线,且 AC = DB. 求证:□ABCD 是矩形.
证明:∵ AB = DC,BC = CB,AC = DB,
∴△ABC≌△DCB.
∴∠ABC =∠DCB.
∵ AB∥CD,
∴∠ABC +∠DCB = 180°.
∴∠ABC = 90°.
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
证一证
矩形的判定定理1:
对角线相等的平行四边形是矩形.
归纳总结
几何语言描述:
在平行四边形 ABCD 中,∵ AC = BD,
∴ 平行四边形 ABCD 是矩形.
A
D
C
B
思考 数学来源于生活,事实上工人师傅为了检验两组对边相等的四边形窗框是否成矩形,其中一种方法就是量一量这个四边形的两条对角线长度,如果对角线长相等,那么窗框一定是矩形,你
现在知道为什么了吗?
对角线相等的平行四边形是矩形.
例题解读
例1 如图,在 □ABCD 中,对角线 AC,BD 相交于点 O,且 OA = OD,∠OAD = 50°.求∠OAB 的度数.
A
B
C
D
O
解:∵ 四边形 ABCD 是平行四边形,
∴ OA = OC = AC,
OB = OD = BD.
又∵ OA = OD,
∴ AC = BD.
∴ 四边形 ABCD 是矩形.
∴∠BAD = 90°.
又∵∠OAD = 50°,
∴∠OAB = 40°.
例2 如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,E、F、G、H 分别是 AO、BO、CO、DO 上的一点,且 AE = BF = CG = DH. 求证:四边形 EFGH 是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵ 四边形 ABCD 是矩形,
∴ AC = BD(矩形的对角线相等),
AO = BO = CO = DO(矩形的对角线互相平分).
∵ AE = BF = CG = DH,
∴ OE = OF = OG = OH.
∴ 四边形 EFGH 是平行四边形,
且 EG = FH.
∴ 四边形 EFGH 是矩形.
知识点2 三个角是直角的四边形是矩形
问题1 上节课我们研究了矩形的四个角,知道它们都是直角,这个性质的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立.
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有两个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
已知:如图,在四边形 ABCD 中,∠A =∠B =∠C = 90°.
求证:四边形 ABCD 是矩形.
证明:∵∠A =∠B =∠C = 90°,
∴∠A +∠B = 180°,∠B +∠C = 180°.
∴ AD∥BC,AB∥CD.
∴ 四边形 ABCD 是平行四边形.
∴ 四边形 ABCD 是矩形.
A
B
C
D
证一证
矩形的判定定理2:
有三个角是直角的四边形是矩形.
归纳总结
几何语言描述:
在四边形 ABCD 中,∵∠A =∠B =∠C = 90°,
∴ 四边形 ABCD 是矩形.
A
B
C
D
思考 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板.为什么?
有三个角是直角的四边形是矩形.
例3 如图,□ ABCD 的四个内角的平分线分别相交于 E、F、G、H,求证:四边形 EFGH 为矩形.
证明:在□ ABCD 中,AD∥BC,
∴∠DAB +∠ABC = 180°.
∵ AE 与 BG 分别为∠DAB、
∠ABC 的平分线,
A
B
D
C
H
E
F
G
∴ 四边形 EFGH 为矩形.
同理可得∠FEH =∠EHG = 90°,
∴∠AFB = 90°.
∴∠GFE = 90°.
∴∠BAF +∠ABF = ∠DAB + ∠ABC = 90°.
例4 如图,在△ABC 中,AB=AC,AD⊥BC,垂足为 D,AN 是△ABC 的外角∠CAM 的平分线,CE⊥AN,垂足为 E,求证:四边形 ADCE 为矩形.
∴∠MAE=∠CAE= ∠CAM.
= (∠BAC+∠CAM )=90°.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵ AN 是△ABC 外角∠CAM 的平分线,
∴∠DAE=∠DAC+∠CAE
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°.
∴ 四边形 ADCE 为矩形.
C
1.如图,直线EF∥MN,PQ交EF,MN于A,C两点,AB,CB,CD,AD分别是∠EAC, ∠MCA, ∠ ACN,∠CAF的角平分线,则四边形ABCD是( )
D
E
F
M
N
Q
P
A
B
C
A.菱形 B.平行四边形 C.矩形 D.不能确定
随堂演练
2.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
D
3.下列命题是真命题的是( )
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形
D.对角线互相垂直的四边形是矩形
C
4. 如图,在△ABC中,AD 为 BC 边上的中线,延长 AD 至 E,使 DE = AD,连接 BE,CE.
(1)试判断四边形 ABEC 的形状;
(2)当△ABC 满足什么条件时,四边形 ABEC 是矩形?
解:(1)四边形 ABEC 是平行四边形.
(2)当△ABC 满足∠BAC=90°时,四边形 ABEC 是矩形.
A
B
C
E
D
5.已知:如图,在 □ ABCD 中,M 是 AD 边的中点,且MB = MC. 求证:四边形 ABCD 是矩形.
证明:在□ ABCD 中,AB = CD,
∵M 是 AD 边的中点,∴MA = MD,且 MB = MC,
即△ABM≌△DCM,∴∠A =∠D.
又∵∠A +∠D = 180°,
∴∠A =∠D = 90°,∴四边形ABCD是矩形.
A
B
D
C
M
课堂小结
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
