19.3.3 正方形 课件 (共31张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 19.3.3 正方形 课件 (共31张PPT) 2023-2024学年数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:34:11 | ||
图片预览






文档简介
(共31张PPT)
第19章 四边形
19.3 矩形、菱形、正方形
19.3.3 正方形
学习目标
1.理解正方形的概念,理解并掌握正方形的性质判定.
2.能够运用正方形的性质和判定解决相关问题.
学习重难点
难点
重点
理解并掌握正方形的性质判定.
能够运用正方形的性质和判定解决相关问题.
情境导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
知识讲解
知识点1 正方形的性质
矩 形
〃
〃
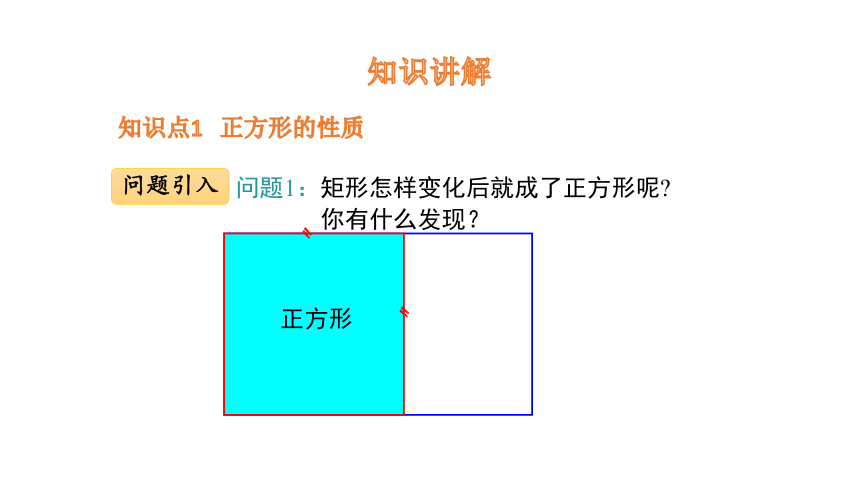
问题1:矩形怎样变化后就成了正方形呢
你有什么发现?
正方形
问题引入
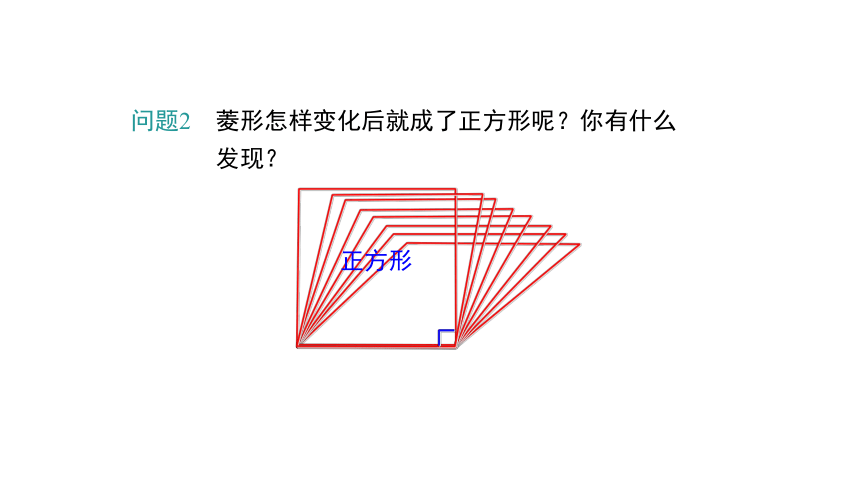
问题2 菱形怎样变化后就成了正方形呢?你有什么
发现?
正方形
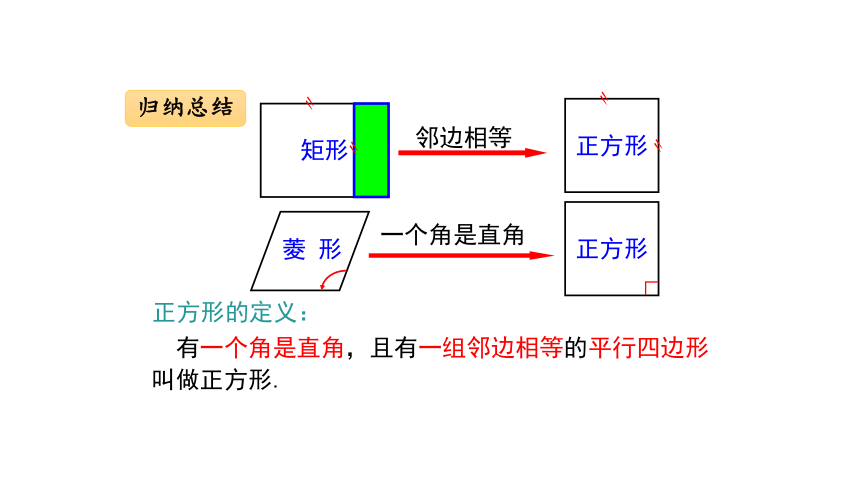
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形的定义:
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
归纳总结
已知:如图,四边形 ABCD 是正方形.
求证:正方形 ABCD 四边相等,四个角都是直角.
A
B
C
D
证明:∵ 四边形 ABCD 是正方形.
∴∠A = 90°,AB = AD (正方形的定义).
又∵ 正方形是平行四边形,
∴ 正方形是矩形 (矩形的定义),
正方形是菱形 (菱形的定义).
∴∠A =∠B =∠C =∠D = 90°,
AB = BC = CD = AD.
证一证
已知:如图,四边形 ABCD 是正方形. 对角线 AC、BD 相交于点 O. 求证:AO = BO = CO = DO,AC⊥BD.
A
B
C
D
O
证明:∵ 正方形 ABCD 是矩形,
∴ AO = BO = CO = DO.
∵ 正方形 ABCD 是菱形,
∴ AC⊥BD.
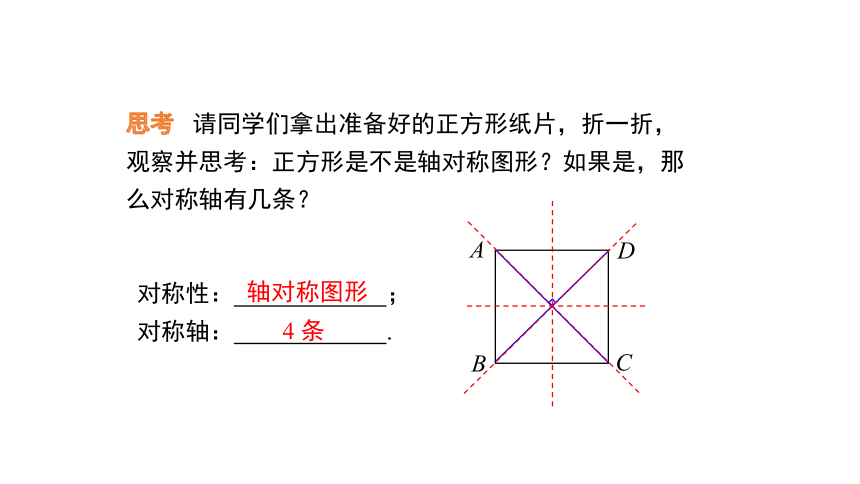
思考 请同学们拿出准备好的正方形纸片,折一折,观察并思考:正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性: ;
对称轴: .
轴对称图形
4 条
A
B
C
D
矩形
菱形
正
方
形
平行四边形
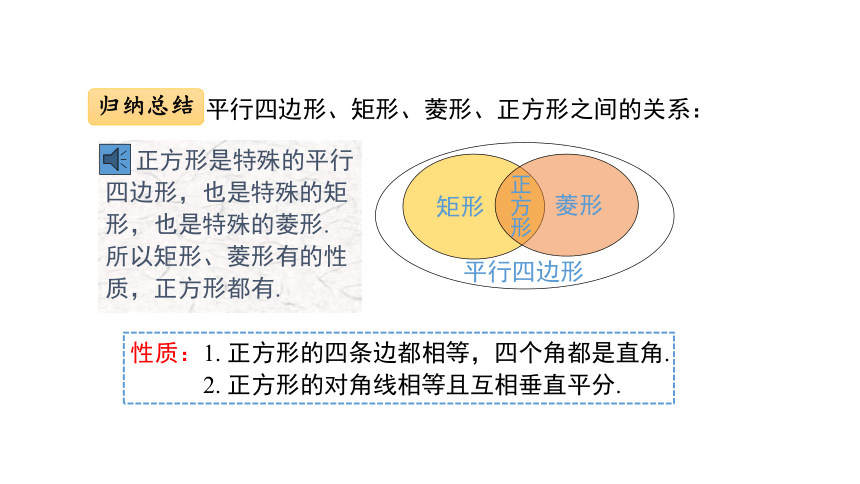
平行四边形、矩形、菱形、正方形之间的关系:
性质:1. 正方形的四条边都相等,四个角都是直角.
2. 正方形的对角线相等且互相垂直平分.
归纳总结
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形. 所以矩形、菱形有的性质,正方形都有.
例题解读
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知: 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证: △ABO、△BCO、△CDO、△DAO是全等的等腰
直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO 都
是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
例2 如图,在正方形 ABCD 中,△BEC 是等边三角形,
求证: ∠EAD =∠EDA = 15°.
证明:∵△BEC 是等边三角形,
∴ BE = CE = BC,∠EBC =∠ECB = 60°.
∵ 四边形 ABCD 是正方形,
∴ AB = BC = CD,∠ABC =∠DCB = 90°.
∴ AB = BE = CE = CD, ∠ABE =∠DCE = 30°.
∴△ABE,△DCE 是等腰三角形.
∴∠BAE =∠BEA =∠CDE =∠CED = 75°.
∴∠EAD =∠EDA = 90° - 75° = 15°.
知识点2 正方形的判定
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
已知:如图,在矩形 ABCD 中,AC,DB 是它的两条对
角线,AC⊥DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是矩形,
∴ AO = CO = BO = DO,∠ADC = 90°.
∵ AC⊥DB,
∴ AD = AB = BC = CD.
∴ 四边形 ABCD 是正方形.
证一证
对角线互相垂直的矩形是正方形.
A
B
C
D
O
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状,量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在菱形 ABCD 中,对角线 AC = DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是菱形,
∴ AB = BC = CD = AD,AC⊥DB.
∵ AC = DB,
∴ AO = BO = CO = DO.
∴△AOD,△AOB,△COD,△BOC 是等腰直角三角形.
∴∠DAB =∠ABC =∠BCD =∠ADC = 90°.
∴ 四边形 ABCD 是正方形.
证一证
对角线相等的菱形是正方形.
A
B
C
D
O
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角/
一组邻边相等/
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等,
且一内角是直角
例3 在正方形 ABCD 中,点 E、F、M、N 分别在各边上,且 AE = BF = CM = DN.
求证:四边形 EFMN 是正方形.
证明:∵ 四边形 ABCD 是正方形,
∴ AB = BC = CD = DA,∠A =∠B =∠C =∠D = 90°.
∵ AE = BF = CM = DN,∴ AN = BE = CF = DM.
分析:由已知可证△AEN≌△BFE≌
△CMF≌△DNM,得四边形 EFMN 是菱形,再证有一个角是直角即可.
在△AEN、△BFE、△CMF、△DNM 中,
AE = BF = CM = DN,
∠A =∠B =∠C =∠D,
AN = BE = CF = DM,
∴△AEN≌△BFE≌△CMF≌△DNM.
∴ EN = FE = MF = NM,∠ANE =∠BEF.
∴ 四边形 EFMN 是菱形.
又∠NEF = 180° - (∠AEN +∠BEF )
= 180° - (∠AEN +∠ANE) = 180° - 90° = 90°.
∴ 四边形 EFMN 是正方形.
证明:∵ DE⊥AC,DF⊥BC,
∴∠DEC =∠DFC = 90°.
又∵∠C = 90°,
∴ 四边形 CEDF 是矩形.
过点 D 作 DG⊥AB 于点 G.
∵ AD 是∠CAB 的平分线,
∴ DE = DG. 同理,DG = DF,∴ DE = DF.
∴ 四边形 CEDF 为正方形.
例4 如图,在 Rt△ABC 中,∠C = 90°,∠A、∠B 的平分线交于点 D,DE⊥AC 于点 E,DF⊥BC 于点 F. 求证:四边形 CEDF 为正方形.
A
B
C
D
E
F
G
例5 如图,EG,FH 过正方形 ABCD 的对角线交点 O,且 EG⊥FH. 求证:四边形 EFGH 是正方形.
证明:∵ 四边形 ABCD 为正方形,
∴ OB = OC,∠ABO =∠BCO = 45°,
∠BOC = 90° =∠COH +∠BOH.
∵ EG⊥FH,
∴∠BOE +∠BOH = 90°.
∴∠COH =∠BOE.
∴△CHO≌△BEO. ∴ OE = OH.
同理可证:OE = OF = OG.
B
A
C
D
O
E
H
G
F
∴ OE = OF = OG = OH,
即 EG 与 FH 互相垂直平分.
∴ 四边形 EFGH 为菱形.
∵ EO + GO = FO + HO,即 EG = HF,
∴四边形 EFGH 是正方形.
B
A
C
D
O
E
H
G
F
思考 前面学菱形时我们探究了顺次连接任意四边形各边中点所得的四边形是平行四边形. 顺次连接矩形各边中点能得到菱形,那么顺次连接正方形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
A
B
C
D
A
B
C
D
矩形
正方形
任意四边形
菱形
正方形
E
F
G
H
E
F
G
H
E
F
G
H
平行四边形
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
随堂演练
2.在正方形ABCD 中,E 是对角线AC 上一点,且AE =AB ,
A
D
B
C
O
E
22.5°
则∠EBC 的度数是 .
3. 如图,四边形 ABCD 中,∠ABC = ∠BCD =∠CDA = 90°,请添加一个条件____________________,可得出该四边形是正方形.
AB = BC (答案不唯一)
A
B
C
D
O
4. 已知四边形 ABCD 是平行四边形,再从①AB = BC,②∠ABC = 90°,③AC = BD,④AC⊥BD 四个条件中,选两个作为补充条件后,使得四边形 ABCD 是正方形,其中错误的是_____________(只填写序号).
②③或①④
5. 如图,正方形 ABCD 的边长为 1 cm,AC 为对角线,AE 平分∠BAC,EF⊥AC,求 BE 的长.
解:∵ 四边形 ABCD 为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1 cm.
∵ EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC 是等腰直角三角形. ∴ EF=FC.
∵∠B=∠EFA=90°,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE.
∴ AB=AF=1 cm,BE=EF. ∴ FC=BE.
在 Rt△ABC 中,
∴ FC=AC-AF=( -1) cm. ∴ BE=( -1) cm.
6. 如图,在四边形 ABCD 中,AB = BC ,对角线 BD 平分 ABC,P 是 BD 上一点,过点 P 作 PM AD,PN CD,垂足分别为 M、N.
(1) 求证: ADB = CDB;
(2) 若 ADC = 90°,求证:四边形 MPND 是正方形.
C
A
B
D
P
M
N
证明:(1) ∵ BD 平分∠ABC.
∴∠1 =∠2.
又∵ AB = BC,BD = BD,
∴△ABD≌△CBD (SAS).
∴∠ADB =∠CDB.
1
2
(2)∵ PM⊥AD,PN⊥CD,
∴∠PMD =∠PND = 90°.
又∵∠ADC = 90°,
∴ 四边形 MPND 是矩形.
∵∠ADB =∠CDB,
∴∠ADB = 45°.
∴∠MPD = 45°.
∴ DM = PM.
∴ 四边形 MPND 是正方形.
C
A
B
D
P
M
N
课堂小结
1. 四个角都是直角
2. 四条边都相等
3. 对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
5 种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角
且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
第19章 四边形
19.3 矩形、菱形、正方形
19.3.3 正方形
学习目标
1.理解正方形的概念,理解并掌握正方形的性质判定.
2.能够运用正方形的性质和判定解决相关问题.
学习重难点
难点
重点
理解并掌握正方形的性质判定.
能够运用正方形的性质和判定解决相关问题.
情境导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
知识讲解
知识点1 正方形的性质
矩 形
〃
〃
问题1:矩形怎样变化后就成了正方形呢
你有什么发现?
正方形
问题引入
问题2 菱形怎样变化后就成了正方形呢?你有什么
发现?
正方形
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形的定义:
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
归纳总结
已知:如图,四边形 ABCD 是正方形.
求证:正方形 ABCD 四边相等,四个角都是直角.
A
B
C
D
证明:∵ 四边形 ABCD 是正方形.
∴∠A = 90°,AB = AD (正方形的定义).
又∵ 正方形是平行四边形,
∴ 正方形是矩形 (矩形的定义),
正方形是菱形 (菱形的定义).
∴∠A =∠B =∠C =∠D = 90°,
AB = BC = CD = AD.
证一证
已知:如图,四边形 ABCD 是正方形. 对角线 AC、BD 相交于点 O. 求证:AO = BO = CO = DO,AC⊥BD.
A
B
C
D
O
证明:∵ 正方形 ABCD 是矩形,
∴ AO = BO = CO = DO.
∵ 正方形 ABCD 是菱形,
∴ AC⊥BD.
思考 请同学们拿出准备好的正方形纸片,折一折,观察并思考:正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性: ;
对称轴: .
轴对称图形
4 条
A
B
C
D
矩形
菱形
正
方
形
平行四边形
平行四边形、矩形、菱形、正方形之间的关系:
性质:1. 正方形的四条边都相等,四个角都是直角.
2. 正方形的对角线相等且互相垂直平分.
归纳总结
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形. 所以矩形、菱形有的性质,正方形都有.
例题解读
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知: 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证: △ABO、△BCO、△CDO、△DAO是全等的等腰
直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO 都
是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
例2 如图,在正方形 ABCD 中,△BEC 是等边三角形,
求证: ∠EAD =∠EDA = 15°.
证明:∵△BEC 是等边三角形,
∴ BE = CE = BC,∠EBC =∠ECB = 60°.
∵ 四边形 ABCD 是正方形,
∴ AB = BC = CD,∠ABC =∠DCB = 90°.
∴ AB = BE = CE = CD, ∠ABE =∠DCE = 30°.
∴△ABE,△DCE 是等腰三角形.
∴∠BAE =∠BEA =∠CDE =∠CED = 75°.
∴∠EAD =∠EDA = 90° - 75° = 15°.
知识点2 正方形的判定
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
已知:如图,在矩形 ABCD 中,AC,DB 是它的两条对
角线,AC⊥DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是矩形,
∴ AO = CO = BO = DO,∠ADC = 90°.
∵ AC⊥DB,
∴ AD = AB = BC = CD.
∴ 四边形 ABCD 是正方形.
证一证
对角线互相垂直的矩形是正方形.
A
B
C
D
O
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状,量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在菱形 ABCD 中,对角线 AC = DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是菱形,
∴ AB = BC = CD = AD,AC⊥DB.
∵ AC = DB,
∴ AO = BO = CO = DO.
∴△AOD,△AOB,△COD,△BOC 是等腰直角三角形.
∴∠DAB =∠ABC =∠BCD =∠ADC = 90°.
∴ 四边形 ABCD 是正方形.
证一证
对角线相等的菱形是正方形.
A
B
C
D
O
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角/
一组邻边相等/
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等,
且一内角是直角
例3 在正方形 ABCD 中,点 E、F、M、N 分别在各边上,且 AE = BF = CM = DN.
求证:四边形 EFMN 是正方形.
证明:∵ 四边形 ABCD 是正方形,
∴ AB = BC = CD = DA,∠A =∠B =∠C =∠D = 90°.
∵ AE = BF = CM = DN,∴ AN = BE = CF = DM.
分析:由已知可证△AEN≌△BFE≌
△CMF≌△DNM,得四边形 EFMN 是菱形,再证有一个角是直角即可.
在△AEN、△BFE、△CMF、△DNM 中,
AE = BF = CM = DN,
∠A =∠B =∠C =∠D,
AN = BE = CF = DM,
∴△AEN≌△BFE≌△CMF≌△DNM.
∴ EN = FE = MF = NM,∠ANE =∠BEF.
∴ 四边形 EFMN 是菱形.
又∠NEF = 180° - (∠AEN +∠BEF )
= 180° - (∠AEN +∠ANE) = 180° - 90° = 90°.
∴ 四边形 EFMN 是正方形.
证明:∵ DE⊥AC,DF⊥BC,
∴∠DEC =∠DFC = 90°.
又∵∠C = 90°,
∴ 四边形 CEDF 是矩形.
过点 D 作 DG⊥AB 于点 G.
∵ AD 是∠CAB 的平分线,
∴ DE = DG. 同理,DG = DF,∴ DE = DF.
∴ 四边形 CEDF 为正方形.
例4 如图,在 Rt△ABC 中,∠C = 90°,∠A、∠B 的平分线交于点 D,DE⊥AC 于点 E,DF⊥BC 于点 F. 求证:四边形 CEDF 为正方形.
A
B
C
D
E
F
G
例5 如图,EG,FH 过正方形 ABCD 的对角线交点 O,且 EG⊥FH. 求证:四边形 EFGH 是正方形.
证明:∵ 四边形 ABCD 为正方形,
∴ OB = OC,∠ABO =∠BCO = 45°,
∠BOC = 90° =∠COH +∠BOH.
∵ EG⊥FH,
∴∠BOE +∠BOH = 90°.
∴∠COH =∠BOE.
∴△CHO≌△BEO. ∴ OE = OH.
同理可证:OE = OF = OG.
B
A
C
D
O
E
H
G
F
∴ OE = OF = OG = OH,
即 EG 与 FH 互相垂直平分.
∴ 四边形 EFGH 为菱形.
∵ EO + GO = FO + HO,即 EG = HF,
∴四边形 EFGH 是正方形.
B
A
C
D
O
E
H
G
F
思考 前面学菱形时我们探究了顺次连接任意四边形各边中点所得的四边形是平行四边形. 顺次连接矩形各边中点能得到菱形,那么顺次连接正方形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
A
B
C
D
A
B
C
D
矩形
正方形
任意四边形
菱形
正方形
E
F
G
H
E
F
G
H
E
F
G
H
平行四边形
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
随堂演练
2.在正方形ABCD 中,E 是对角线AC 上一点,且AE =AB ,
A
D
B
C
O
E
22.5°
则∠EBC 的度数是 .
3. 如图,四边形 ABCD 中,∠ABC = ∠BCD =∠CDA = 90°,请添加一个条件____________________,可得出该四边形是正方形.
AB = BC (答案不唯一)
A
B
C
D
O
4. 已知四边形 ABCD 是平行四边形,再从①AB = BC,②∠ABC = 90°,③AC = BD,④AC⊥BD 四个条件中,选两个作为补充条件后,使得四边形 ABCD 是正方形,其中错误的是_____________(只填写序号).
②③或①④
5. 如图,正方形 ABCD 的边长为 1 cm,AC 为对角线,AE 平分∠BAC,EF⊥AC,求 BE 的长.
解:∵ 四边形 ABCD 为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1 cm.
∵ EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC 是等腰直角三角形. ∴ EF=FC.
∵∠B=∠EFA=90°,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE.
∴ AB=AF=1 cm,BE=EF. ∴ FC=BE.
在 Rt△ABC 中,
∴ FC=AC-AF=( -1) cm. ∴ BE=( -1) cm.
6. 如图,在四边形 ABCD 中,AB = BC ,对角线 BD 平分 ABC,P 是 BD 上一点,过点 P 作 PM AD,PN CD,垂足分别为 M、N.
(1) 求证: ADB = CDB;
(2) 若 ADC = 90°,求证:四边形 MPND 是正方形.
C
A
B
D
P
M
N
证明:(1) ∵ BD 平分∠ABC.
∴∠1 =∠2.
又∵ AB = BC,BD = BD,
∴△ABD≌△CBD (SAS).
∴∠ADB =∠CDB.
1
2
(2)∵ PM⊥AD,PN⊥CD,
∴∠PMD =∠PND = 90°.
又∵∠ADC = 90°,
∴ 四边形 MPND 是矩形.
∵∠ADB =∠CDB,
∴∠ADB = 45°.
∴∠MPD = 45°.
∴ DM = PM.
∴ 四边形 MPND 是正方形.
C
A
B
D
P
M
N
课堂小结
1. 四个角都是直角
2. 四条边都相等
3. 对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
5 种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角
且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
