20.2.1 第1课时 平均数 课件 (共22张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 20.2.1 第1课时 平均数 课件 (共22张PPT) 2023-2024学年数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:35:06 | ||
图片预览







文档简介
(共22张PPT)
第 20章 数据的初步分析
20.2 数据的集中趋势与离散程度
20.2.1数据的集中趋势
第1课时 平均数
学习目标
1.了解平均数和加权平均数的含义、区别及联系.
2.应用平均数和加权平均数的相关知识解决实际问题.
学习重难点
应用平均数和加权平均数的相关知识解决实际问题.
应用平均数和加权平均数的相关知识解决实际问题.
难点
重点
导入新知
在篮球比赛中,队员的身高、年龄都是影响球队实力的因素,
如何衡量两个球队队员的身高?怎样理解“甲队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”?
知识讲解
知识点1 平均数
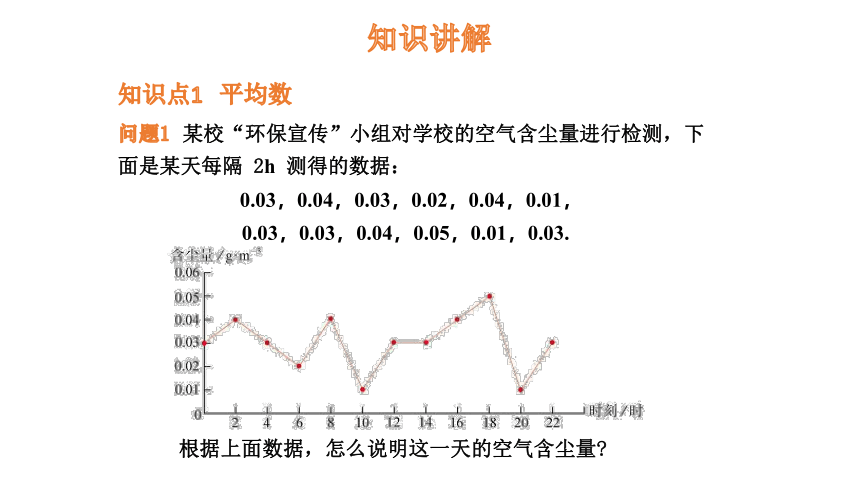
根据上面数据,怎么说明这一天的空气含尘量
问题1 某校“环保宣传”小组对学校的空气含尘量进行检测,下面是某天每隔 2h 测得的数据:
0.03,0.04,0.03,0.02,0.04,0.01,
0.03,0.03,0.04,0.05,0.01,0.03.
思考 在小学我们对平均数有所认识,你能简单的说出平均数的概念吗
用来反映该日空气含尘量的一般状况.
计算上述数据的平均数:
1
12
×(0.03+0.04+0.03+0.02+0.04+0.01+0.03
+0.03+0.04+0.05+0.01+0.03)
我们说学校这一天的空气含尘量平均为0.03g/m3.
=0.03
(g/m3)
把这个平均数作为这组数据的一个代表,
所得的商,
平均数
是指一组数据的总和
除以
这组数据的个数
简称平均数或均数.
来作为刻画它的集中趋势的一种方法;
一般的,如果有n个数据
总结归纳
x1,x2,x3,···,xn
那么
1
n
(x1+x2+x3+···+xn)
即
就是这组数据的平均数,
用“ ”表示,
1
n
(x1+x2+x3+···+xn)
=
平均数是反映数据的平均水平的一个特征量.
对于一组数据,
我们常用平均数
平均数的定义:
①
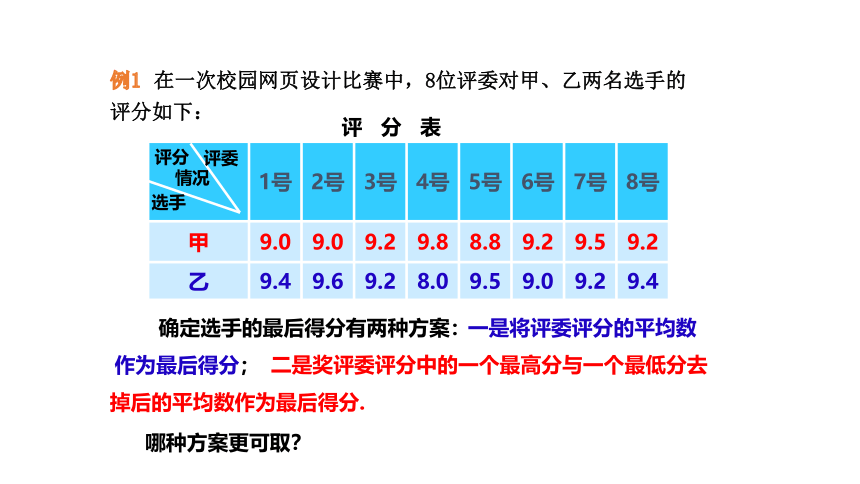
一是将评委评分的平均数作为最后得分;
例1 在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分如下:
评 分 表
1号 2号 3号 4号 5号 6号 7号 8号
甲 9.0 9.0 9.2 9.8 8.8 9.2 9.5 9.2
乙 9.4 9.6 9.2 8.0 9.5 9.0 9.2 9.4
评委
评分
情况
选手
确定选手的最后得分有两种方案:
哪种方案更可取?
二是奖评委评分中的一个最高分与一个最低分去掉后的平均数作为最后得分.
解:
x甲
(8.8+9.0×2+9.2×3+9.5+9.8)
=
1
8
≈ 9.21 (分)
x乙
(8.0+9.0+9.2×2+9.4×2+9.5+9.6)
=
1
8
≈ 9.16 (分)
这时,甲的成绩比乙高.
按方案二计算甲、乙的最后得分为
y甲
(9.0×2+9.2×3+9.5)
=
1
6
≈ 9.18 (分)
y乙
(9.0+9.2×2+9.4×2+9.5)
=
1
6
≈ 9.28 (分)
这时,乙的成绩比甲高.
按方案一计算甲、乙的最后得分为
我们发现有5位评委对甲的评分不高于乙,
将上面的得分与表中的数据相比较,
方案二的结果表明乙的成绩比甲的高,
这表明多数人认为乙的成绩比较好.
因此,方案二评定选手的最后得分比较可取.
与大多数评委的观点相符.
通过对上题的解决,你能说出平均数的大小与什么有关吗?
若这组数据中的一个数据变小,
如果这组数据中的一个数据变大,
平均数的大小与一组数据的每个数据都有关系,
其平均数将变大;
平均数将变小.
交流
只计算余下的数据的平均数,
平均数的缺点:
用平均数作为一组数据的代表,
想一想怎样避免这个缺点?
如某些评奖比赛的计分,通常去掉一个最高分和一个最低分.
容易受到个别极端数值的影响.
为了消除这种现象,可将少数极端数据去掉,
并把所得的结果作为全部数据的平均数.
知识点2 加权平均数
例 2 某校在招聘新教师时以考评成绩确定人选. 甲、乙两位高校毕业生的各项考评成绩如下表:
考评项目 成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
(1) 如果学校将教学设计、课堂教学和答辩按1:3:1的比例来计算各人的考评成绩,那么谁会被录用
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的成绩,那么谁会被录用?
甲的考评成绩为:
乙的考评成绩为:
1+3+1
90×1+85×3+90×1
=87
(分)
1+3+1
80×1+92×3+83×1
=87.8
(分)
解:(1)
因此,乙会被录用.
甲的考评成绩为:
乙的考评成绩为:
90×30%+85×50%+90×20%
=87.5 (分)
80×30%+92×50%+83×20%
=86.6(分)
(2)
因此,甲会被录用.
各个指标的重要程度不一样,考评的结果也就不同.
上例中是用什么来表示各个指标的重要程度?
(1)是用各项所占比例的形式来表示各个指标的重要程度的.
(2)是用各项所占百分比的形式来表示各个指标的重要程度的.
它们都是用来衡量各项考评成绩在总评分中所占权重”,“权重”不一样,结果就不一样.
交流
这n个数据的加权平均数.
在总结果中的比重(如例2),
一般地,对上面的求平均数,可统一用下面的公式:
我们称其为各数据的权,
其中f1,f2,f3,…,fk
分别表示数据
x1,x2,x3,…,xk
出现的次数(如例1),
或者
表示数据x1,x2,x3,…,xk
②
叫做
通过例2,我们可以看出数据的权能反映数据的相对“重要程度”.
总结归纳
f1=1,f2=1,f3=1,…,fk=1时,
公式②和公式①有什么关系?
公式①是公式②的一种特殊形式,
即当
公式②就是公式①.
1
n
(x1+x2+x3+········+xn)
=
①
②
平均数:
加权平均数:
思考
随堂演练
1.某校健美操队共有10名队员,统计队员的年龄情况,结果如下:
13岁3人,14岁5人,15岁2人.该健美操队队员的平均年龄为 ( )
A.14.2岁 B.14.1岁 C.13.9岁 D.13.7岁
C
2. 小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
D
3.某种蔬菜按品质分成三个等级销售,
销售情况如下表:
则售出蔬菜的平均单价为_____________.
等级 单价(元/kg) 销售量(kg)
一等 5.0 20
二等 4.5 40
三等 4.0 40
4.4元/kg
4. 甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A.3.88元 B.4.3元 C.8.7元 D.8.8元
A
5.某商场招聘员工一名,现有甲、乙两人竞聘.通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示.
(1)若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,计算这两名应试者的平均成绩.从成绩看,应该录取谁
(2)若商场需要招聘电脑收银员,计算机、语言、商品知识成绩分别占50%,
30%,20%,计算这两名应试者的平均成绩.从成绩看,应该录取谁
应试者 计算机 语言 商品知识
甲 70 50 80
乙 50 60 85
解:(1)甲的平均成绩:=69(分),
乙的平均成绩:=70.5(分),
因为70.5>69,所以商场应该录取乙.
(2)甲的平均成绩:70×50%+50×30%+80×20%=66(分),
乙的平均成绩:50×50%+60×30%+85×20%=60(分),
因为66>60,所以商场应该录取甲.
课堂小结
平均数
平均数
加权平均数
第 20章 数据的初步分析
20.2 数据的集中趋势与离散程度
20.2.1数据的集中趋势
第1课时 平均数
学习目标
1.了解平均数和加权平均数的含义、区别及联系.
2.应用平均数和加权平均数的相关知识解决实际问题.
学习重难点
应用平均数和加权平均数的相关知识解决实际问题.
应用平均数和加权平均数的相关知识解决实际问题.
难点
重点
导入新知
在篮球比赛中,队员的身高、年龄都是影响球队实力的因素,
如何衡量两个球队队员的身高?怎样理解“甲队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”?
知识讲解
知识点1 平均数
根据上面数据,怎么说明这一天的空气含尘量
问题1 某校“环保宣传”小组对学校的空气含尘量进行检测,下面是某天每隔 2h 测得的数据:
0.03,0.04,0.03,0.02,0.04,0.01,
0.03,0.03,0.04,0.05,0.01,0.03.
思考 在小学我们对平均数有所认识,你能简单的说出平均数的概念吗
用来反映该日空气含尘量的一般状况.
计算上述数据的平均数:
1
12
×(0.03+0.04+0.03+0.02+0.04+0.01+0.03
+0.03+0.04+0.05+0.01+0.03)
我们说学校这一天的空气含尘量平均为0.03g/m3.
=0.03
(g/m3)
把这个平均数作为这组数据的一个代表,
所得的商,
平均数
是指一组数据的总和
除以
这组数据的个数
简称平均数或均数.
来作为刻画它的集中趋势的一种方法;
一般的,如果有n个数据
总结归纳
x1,x2,x3,···,xn
那么
1
n
(x1+x2+x3+···+xn)
即
就是这组数据的平均数,
用“ ”表示,
1
n
(x1+x2+x3+···+xn)
=
平均数是反映数据的平均水平的一个特征量.
对于一组数据,
我们常用平均数
平均数的定义:
①
一是将评委评分的平均数作为最后得分;
例1 在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分如下:
评 分 表
1号 2号 3号 4号 5号 6号 7号 8号
甲 9.0 9.0 9.2 9.8 8.8 9.2 9.5 9.2
乙 9.4 9.6 9.2 8.0 9.5 9.0 9.2 9.4
评委
评分
情况
选手
确定选手的最后得分有两种方案:
哪种方案更可取?
二是奖评委评分中的一个最高分与一个最低分去掉后的平均数作为最后得分.
解:
x甲
(8.8+9.0×2+9.2×3+9.5+9.8)
=
1
8
≈ 9.21 (分)
x乙
(8.0+9.0+9.2×2+9.4×2+9.5+9.6)
=
1
8
≈ 9.16 (分)
这时,甲的成绩比乙高.
按方案二计算甲、乙的最后得分为
y甲
(9.0×2+9.2×3+9.5)
=
1
6
≈ 9.18 (分)
y乙
(9.0+9.2×2+9.4×2+9.5)
=
1
6
≈ 9.28 (分)
这时,乙的成绩比甲高.
按方案一计算甲、乙的最后得分为
我们发现有5位评委对甲的评分不高于乙,
将上面的得分与表中的数据相比较,
方案二的结果表明乙的成绩比甲的高,
这表明多数人认为乙的成绩比较好.
因此,方案二评定选手的最后得分比较可取.
与大多数评委的观点相符.
通过对上题的解决,你能说出平均数的大小与什么有关吗?
若这组数据中的一个数据变小,
如果这组数据中的一个数据变大,
平均数的大小与一组数据的每个数据都有关系,
其平均数将变大;
平均数将变小.
交流
只计算余下的数据的平均数,
平均数的缺点:
用平均数作为一组数据的代表,
想一想怎样避免这个缺点?
如某些评奖比赛的计分,通常去掉一个最高分和一个最低分.
容易受到个别极端数值的影响.
为了消除这种现象,可将少数极端数据去掉,
并把所得的结果作为全部数据的平均数.
知识点2 加权平均数
例 2 某校在招聘新教师时以考评成绩确定人选. 甲、乙两位高校毕业生的各项考评成绩如下表:
考评项目 成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
(1) 如果学校将教学设计、课堂教学和答辩按1:3:1的比例来计算各人的考评成绩,那么谁会被录用
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的成绩,那么谁会被录用?
甲的考评成绩为:
乙的考评成绩为:
1+3+1
90×1+85×3+90×1
=87
(分)
1+3+1
80×1+92×3+83×1
=87.8
(分)
解:(1)
因此,乙会被录用.
甲的考评成绩为:
乙的考评成绩为:
90×30%+85×50%+90×20%
=87.5 (分)
80×30%+92×50%+83×20%
=86.6(分)
(2)
因此,甲会被录用.
各个指标的重要程度不一样,考评的结果也就不同.
上例中是用什么来表示各个指标的重要程度?
(1)是用各项所占比例的形式来表示各个指标的重要程度的.
(2)是用各项所占百分比的形式来表示各个指标的重要程度的.
它们都是用来衡量各项考评成绩在总评分中所占权重”,“权重”不一样,结果就不一样.
交流
这n个数据的加权平均数.
在总结果中的比重(如例2),
一般地,对上面的求平均数,可统一用下面的公式:
我们称其为各数据的权,
其中f1,f2,f3,…,fk
分别表示数据
x1,x2,x3,…,xk
出现的次数(如例1),
或者
表示数据x1,x2,x3,…,xk
②
叫做
通过例2,我们可以看出数据的权能反映数据的相对“重要程度”.
总结归纳
f1=1,f2=1,f3=1,…,fk=1时,
公式②和公式①有什么关系?
公式①是公式②的一种特殊形式,
即当
公式②就是公式①.
1
n
(x1+x2+x3+········+xn)
=
①
②
平均数:
加权平均数:
思考
随堂演练
1.某校健美操队共有10名队员,统计队员的年龄情况,结果如下:
13岁3人,14岁5人,15岁2人.该健美操队队员的平均年龄为 ( )
A.14.2岁 B.14.1岁 C.13.9岁 D.13.7岁
C
2. 小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
D
3.某种蔬菜按品质分成三个等级销售,
销售情况如下表:
则售出蔬菜的平均单价为_____________.
等级 单价(元/kg) 销售量(kg)
一等 5.0 20
二等 4.5 40
三等 4.0 40
4.4元/kg
4. 甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A.3.88元 B.4.3元 C.8.7元 D.8.8元
A
5.某商场招聘员工一名,现有甲、乙两人竞聘.通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示.
(1)若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,计算这两名应试者的平均成绩.从成绩看,应该录取谁
(2)若商场需要招聘电脑收银员,计算机、语言、商品知识成绩分别占50%,
30%,20%,计算这两名应试者的平均成绩.从成绩看,应该录取谁
应试者 计算机 语言 商品知识
甲 70 50 80
乙 50 60 85
解:(1)甲的平均成绩:=69(分),
乙的平均成绩:=70.5(分),
因为70.5>69,所以商场应该录取乙.
(2)甲的平均成绩:70×50%+50×30%+80×20%=66(分),
乙的平均成绩:50×50%+60×30%+85×20%=60(分),
因为66>60,所以商场应该录取甲.
课堂小结
平均数
平均数
加权平均数
