20.2.2 第1课时 方差 课件(共19张PPT) 2023-2024学年数学沪科版八年级下册
文档属性
| 名称 | 20.2.2 第1课时 方差 课件(共19张PPT) 2023-2024学年数学沪科版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:47:21 | ||
图片预览





文档简介
(共19张PPT)
第20章 数据的初步分析
20.2 数据的集中趋势与离散程度
20.2.2 数据的离散程度
第1课时 方差
学习目标
1.了解方差的意义,掌握方差的计算方法.
2.会计算样本的方差并进行简单的决策.
学习重难点
了解方差的意义,掌握方差的计算方法.
1.了解方差的意义,掌握方差的计算方法.
2.会计算样本的方差并进行简单的决策.
难点
重点
复习导入
1、集中趋势统计量:
平均数、
中位数、
众数.
2、平均数计算方法:
1
n
(x1+x2+x3+···+xn)
=
3、加权平均数计算方法:
这n个数据的加权平均数.
在总结果中的比重,
我们称其为各数据的权,
其中f1,f2,f3,…,fk
分别表示数据
x1,x2,x3,…,xk
出现的次数,
或者
表示数据x1,x2,x3,…,xk
叫做
4、中位数的定义:
位于正中间的一个数据
(当数据的个数是偶数时),
一般地,
当将一组数据按大小顺序排列后,
(当数据的个数是奇数时)
或
正中间两个数据的平均数
叫做这组数据的中位数.
n 为奇数时,中间位置是第 个
n为偶数时,中间位置是第 , 个
你知道中间位置如何确定吗
一组数据中
5、众数的定义:
叫做这组数据的众数.
出现次数最多的数据
2
n+1
2
n
2
n
+1
知识讲解
知识点1 方差
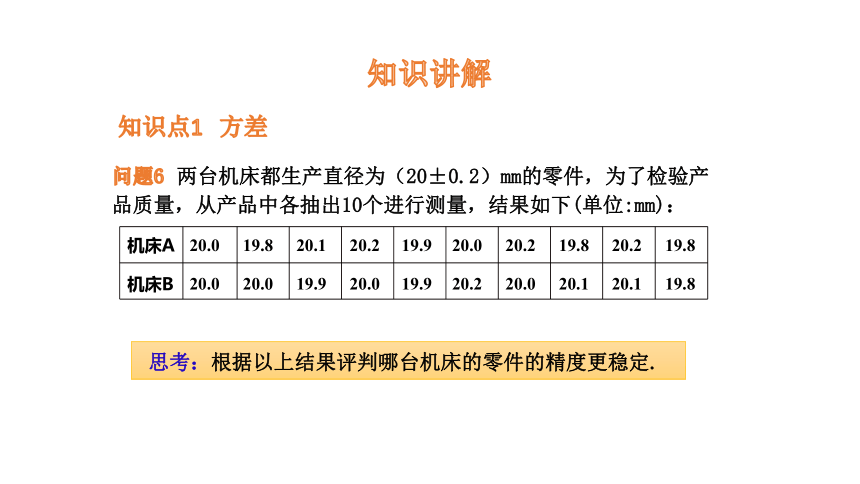
问题6 两台机床都生产直径为(20±0.2)mm的零件,为了检验产品质量,从产品中各抽出10个进行测量,结果如下(单位:mm):
思考:根据以上结果评判哪台机床的零件的精度更稳定.
机床A
20.0
机床B
20.0
19.8
20.0
20.1
19.9
20.2
20.0
20.0
20.2
20.2
20.0
19.8
20.1
19.9
19.9
20.2
20.1
19.8
19.8
( )
+0
从数据集中趋势这个角度
( )
0
-0.2
要比较,首先想到比较两组数据的平均值:
xA
=
1
10
20.0
+
0
-0.2
+0.1
+0.2
-0.1
+0
+0.2
-0.2
+0.2
=20.0(mm)
-0.2
xB
=
1
10
20.0
+
-0.1
+0
-0.1
+0.2
+0
+0.1
+0.1
=20.0(mm)
xA
=
xB
=20.0 mm,
这时就需考察数据的离散程度了.
它们的中位数也都是20.0mm,
很难区分两台机床生产的零件的精度的稳定性,
如何用数量来刻画一组数据的离散程度呢?
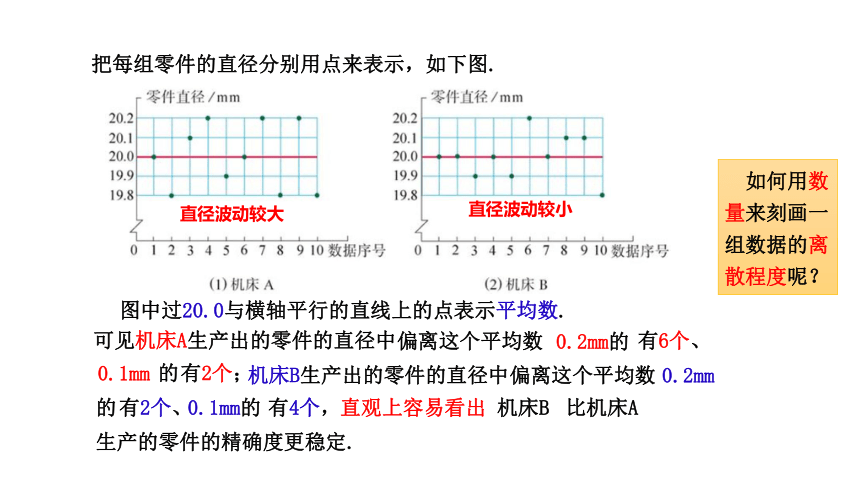
可见机床A生产出的零件的直径中
把每组零件的直径分别用点来表示,如下图.
图中过20.0与横轴平行的直线上的点表示平均数.
0.2mm的
偏离这个平均数
的
0.1mm
机床B生产出的零件的直径中
偏离这个平均数
有6个、
0.2mm
的
有2个、
0.1mm的
有2个;
有4个,
生产的零件的精确度更稳定.
直观上容易看出
机床B
比机床A
直径波动较大
直径波动较小
概念学习
统计学中常用下面的方法:
在一组数据中, 各数据与它们平均数的差的平方的平均数 (即“先平均, 再求差, 然后平方, 最后再平均”) 叫方差.
即 设一组数据是
x1,x2,···,xn,
s2
它们的平均数是 ,
1
n
[ ]
=
x
我们用
( x1 - )2
+( x2 - )2
+( xn - )2
x
x
+···
x
来衡量这组数据的离散程度,
并把它叫做这组数据的
方差.
知识拓展:
反映的是数据在平均数附近波动的情况.
方差越小,
方差是用来衡量一组数据波动大小的重要量,
一般地,
方差越大,
该组数据的波动就越大
(离散程度大),
该组数据的波动就越小
(离散程度小).
① 方差的作用:
才利用方差来判断它们的波动情况.
② 方差的适用条件:
当两组数据的平均数相等或相近时,
比机床B生产的10个零件直径
下面通过计算方差,
的精确度更稳定.
来评判问题中
机床A和机床B
哪台生产的
零件
前面已经算得A,B两组数的平均数,于是
1
10
[ ]
=
(20 -20)2
+ ···
+(19.8-20)2
+(19.8-20)2
=
1
10
[ ]
02
+ ···
+(-0.20)2
+(-0.20)2
=
1
10
×0.26
=0.026
(mm2)
1
10
[ ]
=
(20 -20)2
+ ···
+(20-20)2
+(19.8-20)2
=
1
10
[ ]
02
+ ···
+02
+(-0.20)2
=
1
10
×0.12
=0.012
(mm2)
由于0.026>0.012,
波动要大.
可知机床A生产的10个零件直径
知识拓展:
方差的单位是所给数据单位的平方.
例题解读
例1 甲、乙两台编织机纺织一种毛衣,在5天中
两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;
乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
解:
所以乙台编织机出的产品的波动性较小.
例2 用计算器求下列数据的方差 (结果保留2位小数):
138 , 156 , 131 , 141 , 128 , 139 , 135 , 130.
解: 按键方法:
(1)设定计算模式. 在打开计算器后, 先按“2ndf ”, 然后按“MODE”1将其设定至“Stat”状态;
(2)按键“2ndf”“DEL”, 清除计算器原先在“Stat”模式下所储存的数据;
(3)数据输入, 依次按以下各键:
输入138, 然后按一下“DATA”; 输入156, 然后按一下“DATA”;
输入131, 然后按一下“DATA”; 输入141, 然后按一下“DATA”;
输入128, 然后按一下“DATA”; 输入139, 然后按一下“DATA”; 输入135, 然后按一下“DATA”; 输入130, 然后按一下“DATA”;
(4)求方差, 在计算器的键盘上, 用“σX”表示一组数据的方差的算术平方根.
按键“RCL”“σX”显示方差的算术平方根: σx=8.302860953
按键“X ”“=”显示方差: ANS2=68.9375
由上可得方差: s2=68.94
随堂演练
1.据统计,某班7个学习小组上周参加“青年大学习”的人数分别为
5,5,6,6,6,7,7.下列说法错误的是 ( )
A.该组数据的中位数是6
B.该组数据的众数是6
C.该组数据的平均数是6
D.该组数据的方差是6
D
2. 在一次定点投篮训练中,五位同学投中的个数分别为3,4,4,6,8,则关于这组数据的说法不正确的是( )
A.平均数是5 B.中位数是6
C.众数是4 D.方差是3.2
B
3.甲、乙、丙、丁四位同学在三次数学测试中,他们成绩的平均分是 =85, =85, =85, =85,方差是s甲2=3.8,s乙2=2.3,s丙2=6.2,s丁2=5.2,则成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
B
4.(1)观察下列各组数据并填空:
A:1 2 3 4 5 =________,sA2=________;
B:11 12 13 14 15 =_______,sB2=_______;
C:10 20 30 40 50 =_______,sC2=_______;
D:3 5 7 9 11 =________,sD2=________;
(2)比较A与B,C,D的计算结果,你能发现什么规律?
A与B比较,B组中各数据比A组中对应各数据多10 , ,方差不变
A与C比较,C组各数据为A组中对应各数据的10倍,
A与D比较,D组各数据为A组中对应各数据的2倍多1, =2 +1 , sD2=22×sA2
3
2
13
2
30
200
7
8
,sC2=102×sA2
(3)若已知一组数据x1,x2,…,xn的平均数为 ,方差为s2,
那么另一组数据3x1-2,3x2-2,…,3xn-2的平均数是
________,方差是________.
课堂小结
方差
定义
计算公式
简单应用
衡量一组数据的离散程度
第20章 数据的初步分析
20.2 数据的集中趋势与离散程度
20.2.2 数据的离散程度
第1课时 方差
学习目标
1.了解方差的意义,掌握方差的计算方法.
2.会计算样本的方差并进行简单的决策.
学习重难点
了解方差的意义,掌握方差的计算方法.
1.了解方差的意义,掌握方差的计算方法.
2.会计算样本的方差并进行简单的决策.
难点
重点
复习导入
1、集中趋势统计量:
平均数、
中位数、
众数.
2、平均数计算方法:
1
n
(x1+x2+x3+···+xn)
=
3、加权平均数计算方法:
这n个数据的加权平均数.
在总结果中的比重,
我们称其为各数据的权,
其中f1,f2,f3,…,fk
分别表示数据
x1,x2,x3,…,xk
出现的次数,
或者
表示数据x1,x2,x3,…,xk
叫做
4、中位数的定义:
位于正中间的一个数据
(当数据的个数是偶数时),
一般地,
当将一组数据按大小顺序排列后,
(当数据的个数是奇数时)
或
正中间两个数据的平均数
叫做这组数据的中位数.
n 为奇数时,中间位置是第 个
n为偶数时,中间位置是第 , 个
你知道中间位置如何确定吗
一组数据中
5、众数的定义:
叫做这组数据的众数.
出现次数最多的数据
2
n+1
2
n
2
n
+1
知识讲解
知识点1 方差
问题6 两台机床都生产直径为(20±0.2)mm的零件,为了检验产品质量,从产品中各抽出10个进行测量,结果如下(单位:mm):
思考:根据以上结果评判哪台机床的零件的精度更稳定.
机床A
20.0
机床B
20.0
19.8
20.0
20.1
19.9
20.2
20.0
20.0
20.2
20.2
20.0
19.8
20.1
19.9
19.9
20.2
20.1
19.8
19.8
( )
+0
从数据集中趋势这个角度
( )
0
-0.2
要比较,首先想到比较两组数据的平均值:
xA
=
1
10
20.0
+
0
-0.2
+0.1
+0.2
-0.1
+0
+0.2
-0.2
+0.2
=20.0(mm)
-0.2
xB
=
1
10
20.0
+
-0.1
+0
-0.1
+0.2
+0
+0.1
+0.1
=20.0(mm)
xA
=
xB
=20.0 mm,
这时就需考察数据的离散程度了.
它们的中位数也都是20.0mm,
很难区分两台机床生产的零件的精度的稳定性,
如何用数量来刻画一组数据的离散程度呢?
可见机床A生产出的零件的直径中
把每组零件的直径分别用点来表示,如下图.
图中过20.0与横轴平行的直线上的点表示平均数.
0.2mm的
偏离这个平均数
的
0.1mm
机床B生产出的零件的直径中
偏离这个平均数
有6个、
0.2mm
的
有2个、
0.1mm的
有2个;
有4个,
生产的零件的精确度更稳定.
直观上容易看出
机床B
比机床A
直径波动较大
直径波动较小
概念学习
统计学中常用下面的方法:
在一组数据中, 各数据与它们平均数的差的平方的平均数 (即“先平均, 再求差, 然后平方, 最后再平均”) 叫方差.
即 设一组数据是
x1,x2,···,xn,
s2
它们的平均数是 ,
1
n
[ ]
=
x
我们用
( x1 - )2
+( x2 - )2
+( xn - )2
x
x
+···
x
来衡量这组数据的离散程度,
并把它叫做这组数据的
方差.
知识拓展:
反映的是数据在平均数附近波动的情况.
方差越小,
方差是用来衡量一组数据波动大小的重要量,
一般地,
方差越大,
该组数据的波动就越大
(离散程度大),
该组数据的波动就越小
(离散程度小).
① 方差的作用:
才利用方差来判断它们的波动情况.
② 方差的适用条件:
当两组数据的平均数相等或相近时,
比机床B生产的10个零件直径
下面通过计算方差,
的精确度更稳定.
来评判问题中
机床A和机床B
哪台生产的
零件
前面已经算得A,B两组数的平均数,于是
1
10
[ ]
=
(20 -20)2
+ ···
+(19.8-20)2
+(19.8-20)2
=
1
10
[ ]
02
+ ···
+(-0.20)2
+(-0.20)2
=
1
10
×0.26
=0.026
(mm2)
1
10
[ ]
=
(20 -20)2
+ ···
+(20-20)2
+(19.8-20)2
=
1
10
[ ]
02
+ ···
+02
+(-0.20)2
=
1
10
×0.12
=0.012
(mm2)
由于0.026>0.012,
波动要大.
可知机床A生产的10个零件直径
知识拓展:
方差的单位是所给数据单位的平方.
例题解读
例1 甲、乙两台编织机纺织一种毛衣,在5天中
两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;
乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
解:
所以乙台编织机出的产品的波动性较小.
例2 用计算器求下列数据的方差 (结果保留2位小数):
138 , 156 , 131 , 141 , 128 , 139 , 135 , 130.
解: 按键方法:
(1)设定计算模式. 在打开计算器后, 先按“2ndf ”, 然后按“MODE”1将其设定至“Stat”状态;
(2)按键“2ndf”“DEL”, 清除计算器原先在“Stat”模式下所储存的数据;
(3)数据输入, 依次按以下各键:
输入138, 然后按一下“DATA”; 输入156, 然后按一下“DATA”;
输入131, 然后按一下“DATA”; 输入141, 然后按一下“DATA”;
输入128, 然后按一下“DATA”; 输入139, 然后按一下“DATA”; 输入135, 然后按一下“DATA”; 输入130, 然后按一下“DATA”;
(4)求方差, 在计算器的键盘上, 用“σX”表示一组数据的方差的算术平方根.
按键“RCL”“σX”显示方差的算术平方根: σx=8.302860953
按键“X ”“=”显示方差: ANS2=68.9375
由上可得方差: s2=68.94
随堂演练
1.据统计,某班7个学习小组上周参加“青年大学习”的人数分别为
5,5,6,6,6,7,7.下列说法错误的是 ( )
A.该组数据的中位数是6
B.该组数据的众数是6
C.该组数据的平均数是6
D.该组数据的方差是6
D
2. 在一次定点投篮训练中,五位同学投中的个数分别为3,4,4,6,8,则关于这组数据的说法不正确的是( )
A.平均数是5 B.中位数是6
C.众数是4 D.方差是3.2
B
3.甲、乙、丙、丁四位同学在三次数学测试中,他们成绩的平均分是 =85, =85, =85, =85,方差是s甲2=3.8,s乙2=2.3,s丙2=6.2,s丁2=5.2,则成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
B
4.(1)观察下列各组数据并填空:
A:1 2 3 4 5 =________,sA2=________;
B:11 12 13 14 15 =_______,sB2=_______;
C:10 20 30 40 50 =_______,sC2=_______;
D:3 5 7 9 11 =________,sD2=________;
(2)比较A与B,C,D的计算结果,你能发现什么规律?
A与B比较,B组中各数据比A组中对应各数据多10 , ,方差不变
A与C比较,C组各数据为A组中对应各数据的10倍,
A与D比较,D组各数据为A组中对应各数据的2倍多1, =2 +1 , sD2=22×sA2
3
2
13
2
30
200
7
8
,sC2=102×sA2
(3)若已知一组数据x1,x2,…,xn的平均数为 ,方差为s2,
那么另一组数据3x1-2,3x2-2,…,3xn-2的平均数是
________,方差是________.
课堂小结
方差
定义
计算公式
简单应用
衡量一组数据的离散程度
