4.6利用相似三角形测高导学案(无答案)
文档属性
| 名称 | 4.6利用相似三角形测高导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 41.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-17 22:36:32 | ||
图片预览

文档简介
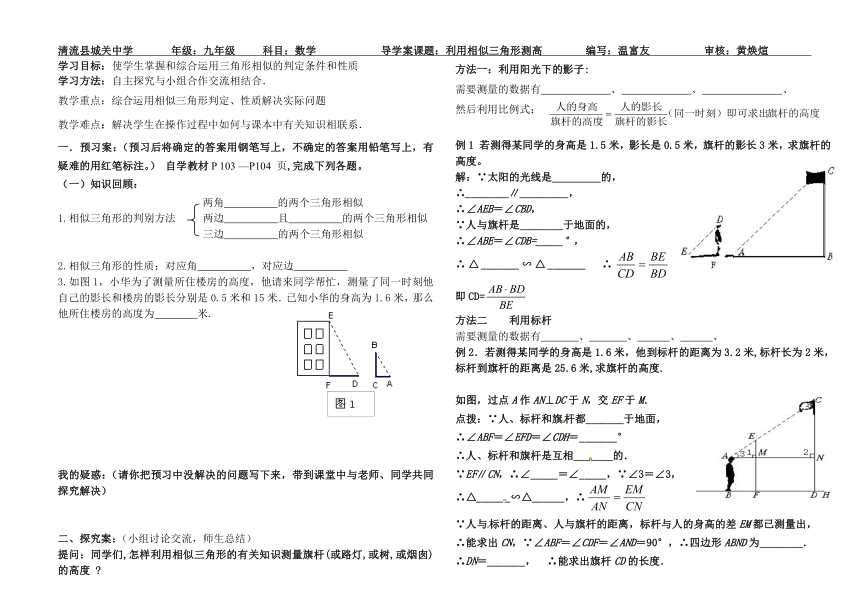
清流县城关中学 年级:九年级 科目:数学 导学案课题:利用相似三角形测高 编写:温富友 审核:黄焕煊
学习目标:使学生掌握和综合运用三角形相似的判定条件和性质
学习方法:自主探究与小组合作交流相结合.
教学重点:综合运用相似三角形判定、性质解决实际问题
教学难点:解决学生在操作过程中如何与课本中有关知识相联系.
一.预习案:(预习后将确定的答案用钢笔写上,不确定的答案用铅笔写上,有疑难的用红笔标注。) 自学教材P 103 —P104 页,完成下列各题。
(一)知识回顾:
两角 的两个三角形相似
1.相似三角形的判别方法 两边 且 的两个三角形相似
三边 的两个三角形相似
2.相似三角形的性质:对应角 ,对应边
3.如图1,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为 米.
我的疑惑:(请你把预习中没解决的问题写下来,带到课堂中与老师、同学共同探究解决)
二、探究案:(小组讨论交流,师生总结)
提问:同学们,怎样利用相似三角形的有关知识测量旗杆(或路灯,或树,或烟囱)的高度
方法一:利用阳光下的影子:
需要测量的数据有 、 、 、
然后利用比例式:
例1 若测得某同学的身高是1.5米,影长是0.5米,旗杆的影长3米,求旗杆的高度。
解:∵太阳的光线是_________的,
∴________∥_________,
∴∠AEB=∠CBD,
∵人与旗杆是________于地面的,
∴∠ABE=∠CDB=_____°,
∴△_______∽△_______ ∴ 即CD=
方法二 利用标杆
需要测量的数据有 、 、 、 、
例2.若测得某同学的身高是1.6米,他到标杆的距离为3.2米,标杆长为2米,
标杆到旗杆的距离是25.6米,求旗杆的高度.
如图,过点A作AN⊥DC于N,交EF于M.
点拨:∵人、标杆和旗杆都_______于地面,
∴∠ABF=∠EFD=∠CDH=_______°
∴人、标杆和旗杆是互相_______的.
∵EF∥CN,∴∠_____=∠_____,∵∠3=∠3,
∴△______∽△______,∴
∵人与标杆的距离、人与旗杆的距离,标杆与人的身高的差EM都已测量出,
∴能求出CN,∵∠ABF=∠CDF=∠AND=90°,∴四边形ABND为________.
∴DN=_______, ∴能求出旗杆CD的长度.
方法三:利用镜子的反射
需要测量的数据有 、 、 、
例3:上述中若同学身高为1.5米,到镜子的距离3米,镜子到旗杆的距离为20米,求旗杆的高度.
三、反馈练习
已知高为4米的旗杆在水平地面的影长是6米,此时测得附近一个建筑物的影子长为18米,则该建筑物的高度是 米。
2、如图,A、B两点分别位于一个池塘的两端,小芳想用绳子测量A、B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A、B点的点C,找到AC、BC的中点D、E,并且DE的长为5m,则A、B两点的距离是多少?
3、某同学想测旗杆的高度,他在某一时刻测得1m长的竹竿竖直时的影长为1.5m,同一时刻测量旗杆影长时,因旗杆靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9m,留在墙上的影长为2m,求旗杆的高度。
四、反思小结(小组讨论交流,师生总结)
综合运用三角形相似的判定条件和性质解决问题时,其方法是:
(1)将实际问题转化为相似三角形问题;
(2)想方设法找出一对相似三角形
(3)根据相似三角形性质,建立比例式,求出相应的量。
五、检测案:
1. 教材P105问题解决:1-4
六、教学反思:
学习目标:使学生掌握和综合运用三角形相似的判定条件和性质
学习方法:自主探究与小组合作交流相结合.
教学重点:综合运用相似三角形判定、性质解决实际问题
教学难点:解决学生在操作过程中如何与课本中有关知识相联系.
一.预习案:(预习后将确定的答案用钢笔写上,不确定的答案用铅笔写上,有疑难的用红笔标注。) 自学教材P 103 —P104 页,完成下列各题。
(一)知识回顾:
两角 的两个三角形相似
1.相似三角形的判别方法 两边 且 的两个三角形相似
三边 的两个三角形相似
2.相似三角形的性质:对应角 ,对应边
3.如图1,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为 米.
我的疑惑:(请你把预习中没解决的问题写下来,带到课堂中与老师、同学共同探究解决)
二、探究案:(小组讨论交流,师生总结)
提问:同学们,怎样利用相似三角形的有关知识测量旗杆(或路灯,或树,或烟囱)的高度
方法一:利用阳光下的影子:
需要测量的数据有 、 、 、
然后利用比例式:
例1 若测得某同学的身高是1.5米,影长是0.5米,旗杆的影长3米,求旗杆的高度。
解:∵太阳的光线是_________的,
∴________∥_________,
∴∠AEB=∠CBD,
∵人与旗杆是________于地面的,
∴∠ABE=∠CDB=_____°,
∴△_______∽△_______ ∴ 即CD=
方法二 利用标杆
需要测量的数据有 、 、 、 、
例2.若测得某同学的身高是1.6米,他到标杆的距离为3.2米,标杆长为2米,
标杆到旗杆的距离是25.6米,求旗杆的高度.
如图,过点A作AN⊥DC于N,交EF于M.
点拨:∵人、标杆和旗杆都_______于地面,
∴∠ABF=∠EFD=∠CDH=_______°
∴人、标杆和旗杆是互相_______的.
∵EF∥CN,∴∠_____=∠_____,∵∠3=∠3,
∴△______∽△______,∴
∵人与标杆的距离、人与旗杆的距离,标杆与人的身高的差EM都已测量出,
∴能求出CN,∵∠ABF=∠CDF=∠AND=90°,∴四边形ABND为________.
∴DN=_______, ∴能求出旗杆CD的长度.
方法三:利用镜子的反射
需要测量的数据有 、 、 、
例3:上述中若同学身高为1.5米,到镜子的距离3米,镜子到旗杆的距离为20米,求旗杆的高度.
三、反馈练习
已知高为4米的旗杆在水平地面的影长是6米,此时测得附近一个建筑物的影子长为18米,则该建筑物的高度是 米。
2、如图,A、B两点分别位于一个池塘的两端,小芳想用绳子测量A、B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A、B点的点C,找到AC、BC的中点D、E,并且DE的长为5m,则A、B两点的距离是多少?
3、某同学想测旗杆的高度,他在某一时刻测得1m长的竹竿竖直时的影长为1.5m,同一时刻测量旗杆影长时,因旗杆靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9m,留在墙上的影长为2m,求旗杆的高度。
四、反思小结(小组讨论交流,师生总结)
综合运用三角形相似的判定条件和性质解决问题时,其方法是:
(1)将实际问题转化为相似三角形问题;
(2)想方设法找出一对相似三角形
(3)根据相似三角形性质,建立比例式,求出相应的量。
五、检测案:
1. 教材P105问题解决:1-4
六、教学反思:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
