7.4.6一元一次方程的应用 课件(共13张PPT) 青岛版数学七年级上册
文档属性
| 名称 | 7.4.6一元一次方程的应用 课件(共13张PPT) 青岛版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 668.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
7.4.6 一元一次方程的应用
(等积变形问题)
学习目标:
重点:找出等量关系,解决实际问题。
难点:运用方程解决与体积变形有关的题.
1、经历运用方程解决实际问题的过程,发展应用数学的意识;
2、熟练运用列方程解应用题的一般步骤列方程;
3、学会列一元一次方程解决与体积变形的应用题。
回顾旧知
常用几何图形的计算公式:
长方形的周长 =
长方形的面积 =
三角形的面积 =
圆的周长=
圆的面积=
长方体的体积 =
圆柱体的体积 =
2πr
πr2
长×宽×高
(长+宽)×2
长 ×宽
底面积×高=π r2h
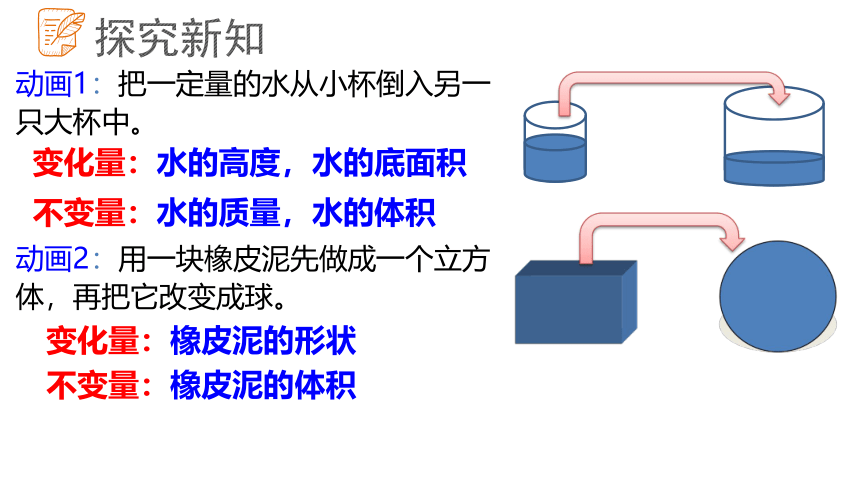
动画1:把一定量的水从小杯倒入另一只大杯中。
动画2:用一块橡皮泥先做成一个立方体,再把它改变成球。
变化量:水的高度,水的底面积
不变量:水的质量,水的体积
变化量:橡皮泥的形状
不变量:橡皮泥的体积
探究新知
探究新知
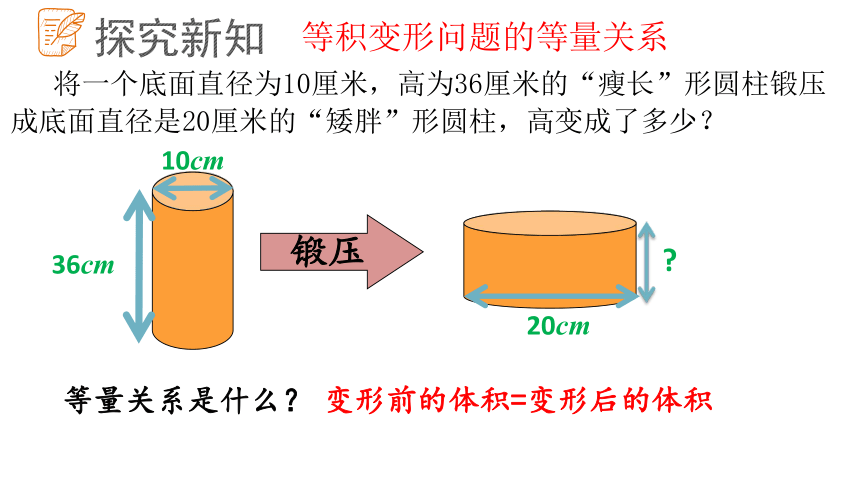
将一个底面直径为10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖”形圆柱,高变成了多少?
锻压
等量关系是什么?
变形前的体积=变形后的体积
10cm
36cm
20cm
等积变形问题的等量关系
探究新知
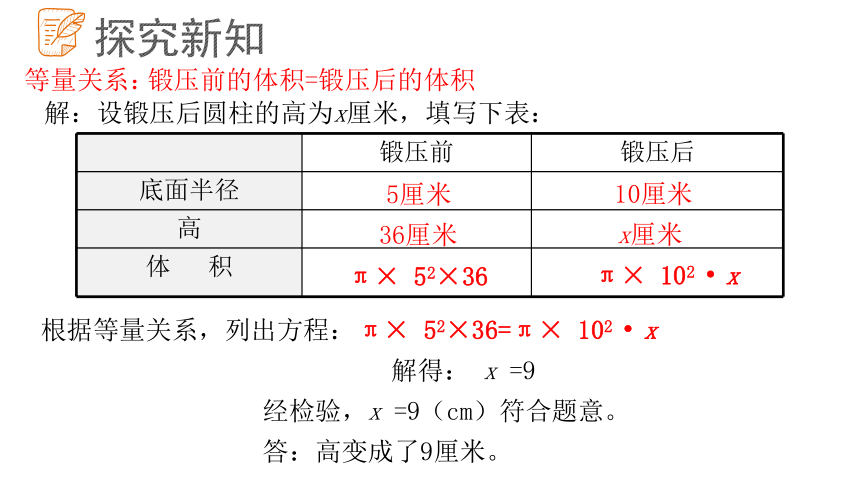
解:设锻压后圆柱的高为x厘米,填写下表:
锻压前 锻压后
底面半径
高
体 积
5厘米
10厘米
36厘米
x厘米
等量关系:
锻压前的体积=锻压后的体积
π× 52×36
π× 102 x
根据等量关系,列出方程:
解得: x =9
π× 52×36=π× 102 x
答:高变成了9厘米。
经检验,x =9(cm)符合题意。
例7:一个圆柱形容器底面半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水,现将一底面半径为2厘米、高18厘米的金属柱竖直放入容器内,容器内的水面将升高多少厘米
分析:1、哪些是已知量,哪些是未知量?
2、等量关系是什么
3、一共几种情况?
典型例题
1、已知量:
圆柱形容器的底面半径和内壁高;
水的高度;
金属柱的底面半径和高
未知量:
水面升高的高度
2、等量关系:加金属柱前容器内水的体积=加金属柱后容器内水的体积
3、两种情况:①水没过金属柱;②水未没过金属柱
例7:一个圆柱形容器底面半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水,现将一底面半径为2厘米、高18厘米的金属柱竖直放入容器内,容器内的水面将升高多少厘米
30cm
3cm
2cm
第一种情况:水没过金属柱,设容器内的水面将升高x厘米
xcm
(x+15)cm
15cm
18cm
典型例题
第一种情况:水没过金属柱,设容器内的水面将升高x厘米
32 15
加金属柱后容器内水的体积:
32 (x+15)- 22 18
典型例题
加金属柱前容器内水的体积:
解:如果容器内放入金属圆柱后,容器内的水面将升高x厘米, 则水面高度为(x+15)厘米.根据题意,得方程为:
32 15= 32 (x+15)- 22 18
解这个方程,得:
x =8
经检验,x=8 (厘米)符合题意。
答:容器内水面将升高8cm。
第二种情况:水尚未没过金属柱,设容器内的水面将升高x厘米
30cm
3cm
2cm
xcm
(x+15)cm
15cm
18cm
例7:一个圆柱形容器底面半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水,现将一底面半径为2厘米、高18厘米的金属柱竖直放入容器内,容器内的水面将升高多少厘米
典型例题
第二种情况:水未没过金属柱,设容器内的水面将升高x厘米
32 15
加金属柱后容器内水的体积:
32 (x+15)- 22 (x+15)
典型例题
加金属柱前容器内水的体积:
解:如果容器内放入金属圆柱后,容器内的水面将升高x厘米, 则水面高度为(x+15)厘米.根据题意,得方程为:
32 15= 32 (x+15)- 22 (x+15)
解这个方程,得:
x = 12
不符合假定,舍弃。
12+15=27
∵27cm>18cm
这表明此时容器内的水面已淹没金属圆柱
列一元一次方程解应用题的一般步骤:
1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数.
2、用代数式表示有关的量.
3、根据等量关系列出方程.
4、解方程,求出未知数的值.
5、检验求得的值是否正确和符合实际情形,并写出答案.
课堂小结
课后作业
作业:
P173 练习、习题7.4
同步练习册
7.4.6 一元一次方程的应用
(等积变形问题)
学习目标:
重点:找出等量关系,解决实际问题。
难点:运用方程解决与体积变形有关的题.
1、经历运用方程解决实际问题的过程,发展应用数学的意识;
2、熟练运用列方程解应用题的一般步骤列方程;
3、学会列一元一次方程解决与体积变形的应用题。
回顾旧知
常用几何图形的计算公式:
长方形的周长 =
长方形的面积 =
三角形的面积 =
圆的周长=
圆的面积=
长方体的体积 =
圆柱体的体积 =
2πr
πr2
长×宽×高
(长+宽)×2
长 ×宽
底面积×高=π r2h
动画1:把一定量的水从小杯倒入另一只大杯中。
动画2:用一块橡皮泥先做成一个立方体,再把它改变成球。
变化量:水的高度,水的底面积
不变量:水的质量,水的体积
变化量:橡皮泥的形状
不变量:橡皮泥的体积
探究新知
探究新知
将一个底面直径为10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖”形圆柱,高变成了多少?
锻压
等量关系是什么?
变形前的体积=变形后的体积
10cm
36cm
20cm
等积变形问题的等量关系
探究新知
解:设锻压后圆柱的高为x厘米,填写下表:
锻压前 锻压后
底面半径
高
体 积
5厘米
10厘米
36厘米
x厘米
等量关系:
锻压前的体积=锻压后的体积
π× 52×36
π× 102 x
根据等量关系,列出方程:
解得: x =9
π× 52×36=π× 102 x
答:高变成了9厘米。
经检验,x =9(cm)符合题意。
例7:一个圆柱形容器底面半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水,现将一底面半径为2厘米、高18厘米的金属柱竖直放入容器内,容器内的水面将升高多少厘米
分析:1、哪些是已知量,哪些是未知量?
2、等量关系是什么
3、一共几种情况?
典型例题
1、已知量:
圆柱形容器的底面半径和内壁高;
水的高度;
金属柱的底面半径和高
未知量:
水面升高的高度
2、等量关系:加金属柱前容器内水的体积=加金属柱后容器内水的体积
3、两种情况:①水没过金属柱;②水未没过金属柱
例7:一个圆柱形容器底面半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水,现将一底面半径为2厘米、高18厘米的金属柱竖直放入容器内,容器内的水面将升高多少厘米
30cm
3cm
2cm
第一种情况:水没过金属柱,设容器内的水面将升高x厘米
xcm
(x+15)cm
15cm
18cm
典型例题
第一种情况:水没过金属柱,设容器内的水面将升高x厘米
32 15
加金属柱后容器内水的体积:
32 (x+15)- 22 18
典型例题
加金属柱前容器内水的体积:
解:如果容器内放入金属圆柱后,容器内的水面将升高x厘米, 则水面高度为(x+15)厘米.根据题意,得方程为:
32 15= 32 (x+15)- 22 18
解这个方程,得:
x =8
经检验,x=8 (厘米)符合题意。
答:容器内水面将升高8cm。
第二种情况:水尚未没过金属柱,设容器内的水面将升高x厘米
30cm
3cm
2cm
xcm
(x+15)cm
15cm
18cm
例7:一个圆柱形容器底面半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水,现将一底面半径为2厘米、高18厘米的金属柱竖直放入容器内,容器内的水面将升高多少厘米
典型例题
第二种情况:水未没过金属柱,设容器内的水面将升高x厘米
32 15
加金属柱后容器内水的体积:
32 (x+15)- 22 (x+15)
典型例题
加金属柱前容器内水的体积:
解:如果容器内放入金属圆柱后,容器内的水面将升高x厘米, 则水面高度为(x+15)厘米.根据题意,得方程为:
32 15= 32 (x+15)- 22 (x+15)
解这个方程,得:
x = 12
不符合假定,舍弃。
12+15=27
∵27cm>18cm
这表明此时容器内的水面已淹没金属圆柱
列一元一次方程解应用题的一般步骤:
1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数.
2、用代数式表示有关的量.
3、根据等量关系列出方程.
4、解方程,求出未知数的值.
5、检验求得的值是否正确和符合实际情形,并写出答案.
课堂小结
课后作业
作业:
P173 练习、习题7.4
同步练习册
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
