五年级数学下册苏教版1.1 等式、方程的含义(课件)(共17张PPT)
文档属性
| 名称 | 五年级数学下册苏教版1.1 等式、方程的含义(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 12:33:40 | ||
图片预览






文档简介
(共17张PPT)
1.1 等式、方程的含义
苏教版小学数学五年级下册
1、初步理解“等式”,“不等式”和“方程”的意义,
并进行辨析,会按要求用方程表示出数量关系。
2、在观察、分析、抽象、概括和交流的过程中
构建数学概念,感受方程的思想。
3、体会在知识探索过程中,与人合作的乐趣,
激发兴趣。
学习重点:认识方程的意义,用方程表示交点的
数量关系。
学习难点:理解方程的意义。
学习目标
一、情境引入:
1、认识天平
刻度盘
砝码
衡梁
左托盘
右托盘
标尺
底座
一、情境引入:
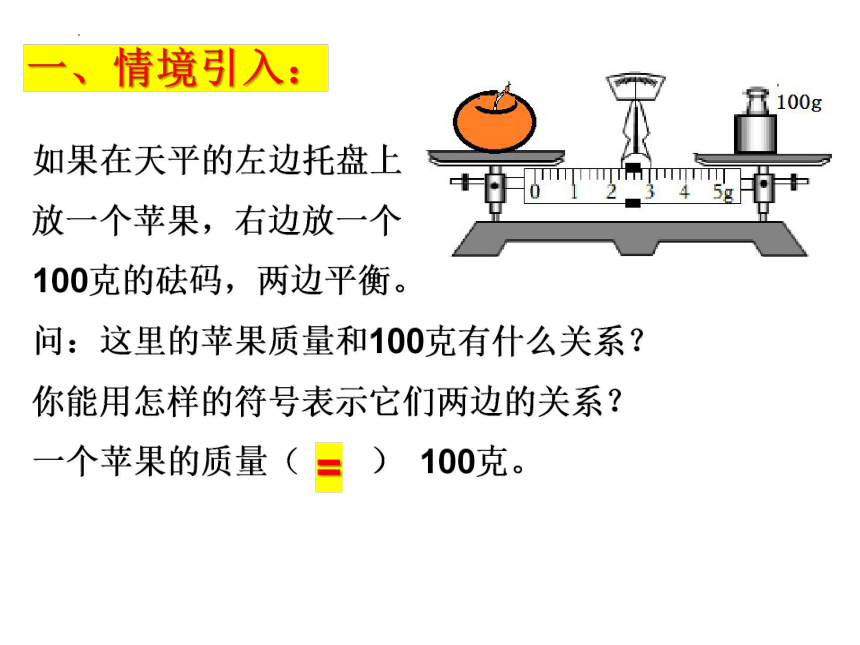
如果在天平的左边托盘上
放一个苹果,右边放一个
100克的砝码,两边平衡。
问:这里的苹果质量和100克有什么关系?
你能用怎样的符号表示它们两边的关系?
一个苹果的质量( ) 100克。
=
一个苹果的质量+一个橘子的质量( ) 100克,
或100克( )一个苹果的质量+一个橘子的质量。
2、如果在天平的左边
加上一个橘子,
天平倾斜,说明什么?
你能用怎样的符号表示
它们两边的关系?
说明:
表示两边相等的式子叫做等式;
表示两边不相等的式子叫做不等式。
>
<
探究新知
1、巩固等式知识:
如图,你能写一个等式吗?
( )+( )=100,
2×( )=100.
50
50
50
2、认识方程:
用式子表示天平两边物体质量的大小关系。
<
x+50
=
天平不平衡(左重右轻)
>
天平不平衡(两边一样重)
x+50
200
天平不平衡(左轻右重)
x+x
=
200
天平不平衡(两边一样重)
这些式子中哪些是等式?
方程一定是等式,而等式不一定是方程。
像x+50=150,2x=200这样
含有未知数的等式是方程。
3、等式与方程的关系:
等式和方程的关系可以用图表示:
试一试:
判断对错。(对的打“√”,错的打“×”)
(1)方程都是等式,但等式不一定是方程。( )
(2)含有未知数的式子叫做方程。 ( )
(3)10=4x-8不是方程。 ( )
(4)等式都是方程,方程都是等式。 ( )
二、例题讲解:例1、下面的式子:(1)9+x=15; (2)30+20=50;
(3)43+13>30; (4)y-9;(5)50÷5=10; (6)x-7<14;
(7)y-23=6; (8)x=2y-1。其中, 是等式, 是方程。(填序号)。
例2、看图形列方程。
3x+25=145
x+240=600
2x+5×2=36
2x+10=100
26x÷2=195
4x+16.5=18.9
三、基础强化:1、下面哪些是方程,在括号里画“√”。(1)x+3=28 ( )(2)32x>64 ( )
(3)56+x-8 ( ) (4)15÷x=1 ( )(5)20-8=12( )(6)24-x=17( )
(7)X=5 ( ) (8)A+4=56 ( )2、 根据“妈妈比小红大26岁”,填写下面的数量关系。( )的年龄+26=( )的年龄;
( )的年龄-26=( )的年龄
3、根据线段图列方程。
4、一个两位数,个位数字为5,十位数字为x,
如果这两位数是54,根据题意,列方程为( )。
四、拓展提高:5、已知a和b都是非零自然数,a+b=100,
那么a、b的积最大是多少?最小是多少?
五、总结反思:
1、等式与方程的含义:
用等于号连接起来的式子叫等式;
含有未知数的等式叫做方程。
2、等式与方程的关系:
方程一定是等式,等式不一定是方程。
六、随堂检测: 看图形,列方程:
1.1 等式、方程的含义
苏教版小学数学五年级下册
1、初步理解“等式”,“不等式”和“方程”的意义,
并进行辨析,会按要求用方程表示出数量关系。
2、在观察、分析、抽象、概括和交流的过程中
构建数学概念,感受方程的思想。
3、体会在知识探索过程中,与人合作的乐趣,
激发兴趣。
学习重点:认识方程的意义,用方程表示交点的
数量关系。
学习难点:理解方程的意义。
学习目标
一、情境引入:
1、认识天平
刻度盘
砝码
衡梁
左托盘
右托盘
标尺
底座
一、情境引入:
如果在天平的左边托盘上
放一个苹果,右边放一个
100克的砝码,两边平衡。
问:这里的苹果质量和100克有什么关系?
你能用怎样的符号表示它们两边的关系?
一个苹果的质量( ) 100克。
=
一个苹果的质量+一个橘子的质量( ) 100克,
或100克( )一个苹果的质量+一个橘子的质量。
2、如果在天平的左边
加上一个橘子,
天平倾斜,说明什么?
你能用怎样的符号表示
它们两边的关系?
说明:
表示两边相等的式子叫做等式;
表示两边不相等的式子叫做不等式。
>
<
探究新知
1、巩固等式知识:
如图,你能写一个等式吗?
( )+( )=100,
2×( )=100.
50
50
50
2、认识方程:
用式子表示天平两边物体质量的大小关系。
<
x+50
=
天平不平衡(左重右轻)
>
天平不平衡(两边一样重)
x+50
200
天平不平衡(左轻右重)
x+x
=
200
天平不平衡(两边一样重)
这些式子中哪些是等式?
方程一定是等式,而等式不一定是方程。
像x+50=150,2x=200这样
含有未知数的等式是方程。
3、等式与方程的关系:
等式和方程的关系可以用图表示:
试一试:
判断对错。(对的打“√”,错的打“×”)
(1)方程都是等式,但等式不一定是方程。( )
(2)含有未知数的式子叫做方程。 ( )
(3)10=4x-8不是方程。 ( )
(4)等式都是方程,方程都是等式。 ( )
二、例题讲解:例1、下面的式子:(1)9+x=15; (2)30+20=50;
(3)43+13>30; (4)y-9;(5)50÷5=10; (6)x-7<14;
(7)y-23=6; (8)x=2y-1。其中, 是等式, 是方程。(填序号)。
例2、看图形列方程。
3x+25=145
x+240=600
2x+5×2=36
2x+10=100
26x÷2=195
4x+16.5=18.9
三、基础强化:1、下面哪些是方程,在括号里画“√”。(1)x+3=28 ( )(2)32x>64 ( )
(3)56+x-8 ( ) (4)15÷x=1 ( )(5)20-8=12( )(6)24-x=17( )
(7)X=5 ( ) (8)A+4=56 ( )2、 根据“妈妈比小红大26岁”,填写下面的数量关系。( )的年龄+26=( )的年龄;
( )的年龄-26=( )的年龄
3、根据线段图列方程。
4、一个两位数,个位数字为5,十位数字为x,
如果这两位数是54,根据题意,列方程为( )。
四、拓展提高:5、已知a和b都是非零自然数,a+b=100,
那么a、b的积最大是多少?最小是多少?
五、总结反思:
1、等式与方程的含义:
用等于号连接起来的式子叫等式;
含有未知数的等式叫做方程。
2、等式与方程的关系:
方程一定是等式,等式不一定是方程。
六、随堂检测: 看图形,列方程:
