数学:2.1.2《平面向量的加法》课件(新人教版a必修4)
文档属性
| 名称 | 数学:2.1.2《平面向量的加法》课件(新人教版a必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 583.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览


文档简介
课件17张PPT。2019/3/13 向量的加法看书 P80~83(限时6分钟)学习目标:
通过实例,掌握向量的加法运算及理解其几何意义。
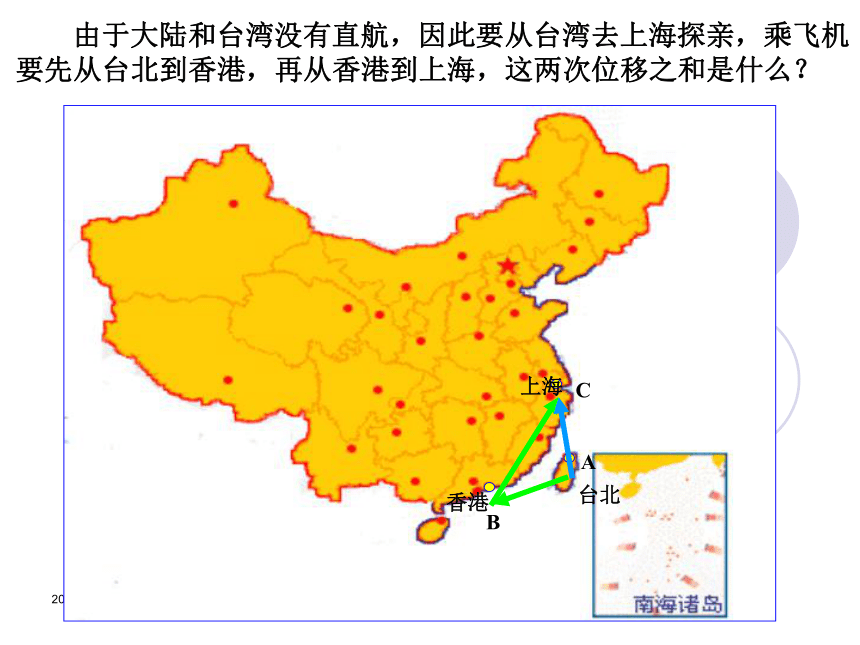
熟练运用加法的“三角形法则”和“平行四边形”法则2019/3/13 由于大陆和台湾没有直航,因此要从台湾去上海探亲,乘飞机
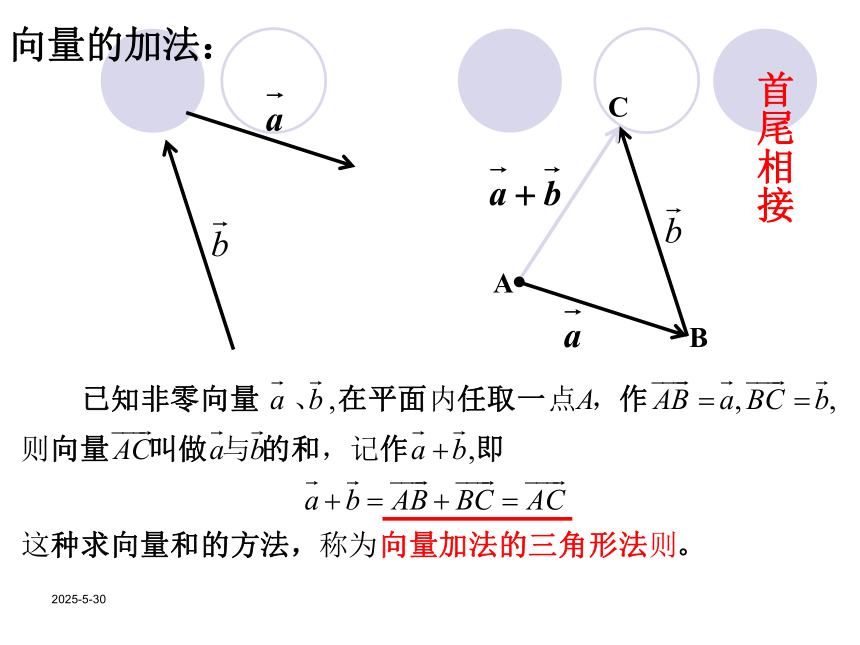
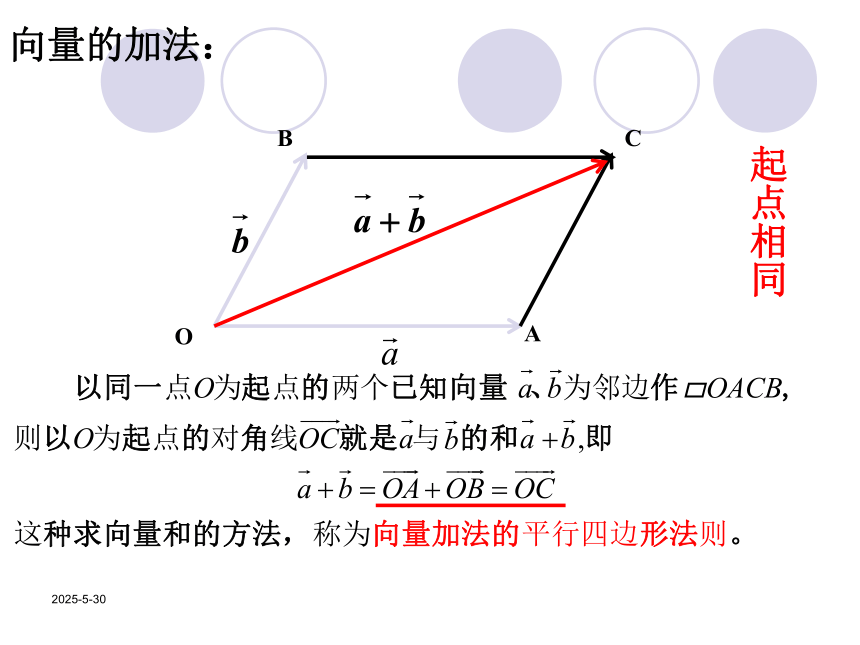
要先从台北到香港,再从香港到上海,这两次位移之和是什么? 台北香港上海ABC2019/3/13向量的加法:CAB首尾相接2019/3/13向量的加法:起点相同2019/3/13对于向量的加法的理解需要注意下面两点:
(1)两个向量的和仍然是向量(简称和向量)
(2)位移的合成是三角形法则的物理模型.
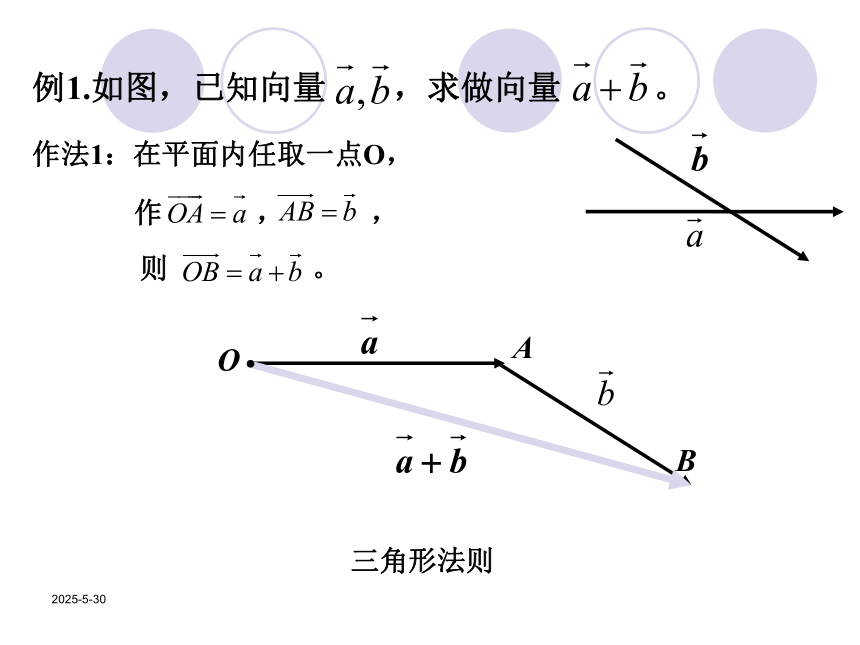
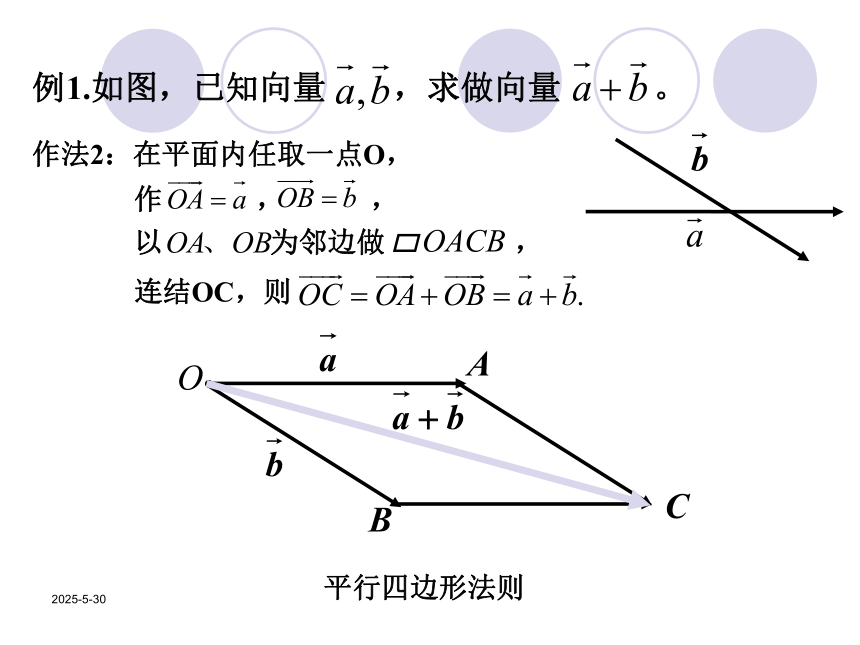
2019/3/13例1.如图,已知向量 ,求做向量 。
则 。 三角形法则作法1:在平面内任取一点O,作 , ,2019/3/13例1.如图,已知向量 ,求做向量 。作法2:在平面内任取一点O,作 , ,以 为邻边做 ,连结OC,则平行四边形法则2019/3/13练习:限时4分钟
P83 1、2探究:
多个向量的运算将如何进行?2019/3/13思考:如果非零向量 、 、 ,满足
则以 为有向线段的三条线段,能构成一个三角形吗?请同学们
总结向量加法的“三角形法则”与“平行四边形”法则的联系与区别。2019/3/132019/3/13思考:如图,当在数轴上表示两个共线向量时,它们的加法和
数的加法有什么关系?(1)(2)BCBC2019/3/132019/3/13B2019/3/13例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。ADBC2019/3/13例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。答:船实际航行速度为4km/h,方向与水的流速间的夹角为60o。ADBC2019/3/13练习:限时2分钟2019/3/13课后作业:
P84练习B 1、3
通过实例,掌握向量的加法运算及理解其几何意义。
熟练运用加法的“三角形法则”和“平行四边形”法则2019/3/13 由于大陆和台湾没有直航,因此要从台湾去上海探亲,乘飞机
要先从台北到香港,再从香港到上海,这两次位移之和是什么? 台北香港上海ABC2019/3/13向量的加法:CAB首尾相接2019/3/13向量的加法:起点相同2019/3/13对于向量的加法的理解需要注意下面两点:
(1)两个向量的和仍然是向量(简称和向量)
(2)位移的合成是三角形法则的物理模型.
2019/3/13例1.如图,已知向量 ,求做向量 。
则 。 三角形法则作法1:在平面内任取一点O,作 , ,2019/3/13例1.如图,已知向量 ,求做向量 。作法2:在平面内任取一点O,作 , ,以 为邻边做 ,连结OC,则平行四边形法则2019/3/13练习:限时4分钟
P83 1、2探究:
多个向量的运算将如何进行?2019/3/13思考:如果非零向量 、 、 ,满足
则以 为有向线段的三条线段,能构成一个三角形吗?请同学们
总结向量加法的“三角形法则”与“平行四边形”法则的联系与区别。2019/3/132019/3/13思考:如图,当在数轴上表示两个共线向量时,它们的加法和
数的加法有什么关系?(1)(2)BCBC2019/3/132019/3/13B2019/3/13例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。ADBC2019/3/13例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。答:船实际航行速度为4km/h,方向与水的流速间的夹角为60o。ADBC2019/3/13练习:限时2分钟2019/3/13课后作业:
P84练习B 1、3
