数学:2.3.1《向量数量积的物理背景与定义》课件(新人教b版必修4)
文档属性
| 名称 | 数学:2.3.1《向量数量积的物理背景与定义》课件(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 421.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览




文档简介
课件24张PPT。计算下列各式课前小测复习思考:
向量的加法
向量的减法
实数与向量的乘法
两个向量的数量积运算结果向量向量向量向量数量积的物理背景与定义学习目标 1、掌握平面向量数量积的物理
背景; 3、掌握平面向量数量积的定义性质及几何意义。 2、理解一个向量在另一个向量
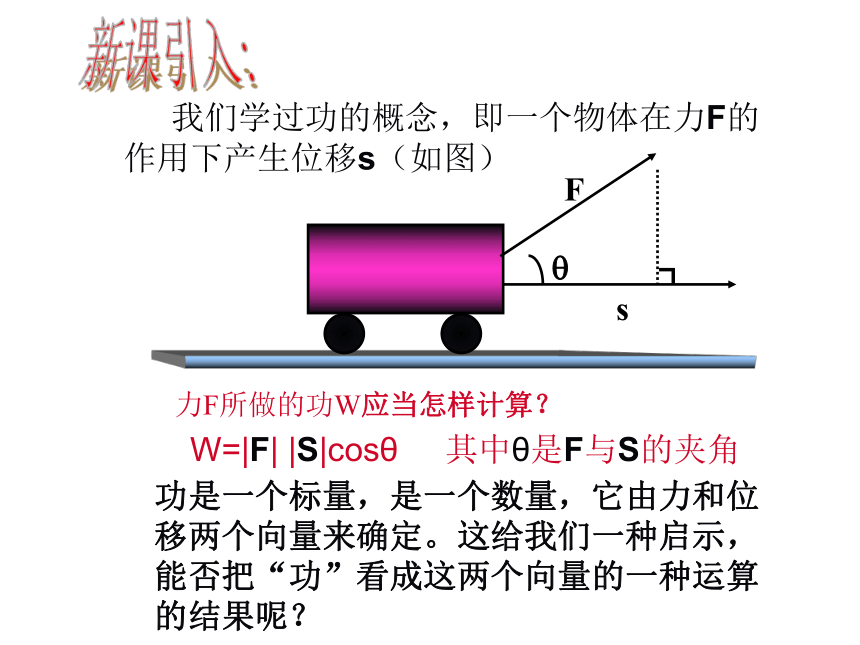
方向上的正投影的概念; 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)
W=|F| |S|cosθ 其中θ是F与S的夹角新课引入:功是一个标量,是一个数量,它由力和位移两个向量来确定。这给我们一种启示,能否把“功”看成这两个向量的一种运算的结果呢?力F所做的功W应当怎样计算?
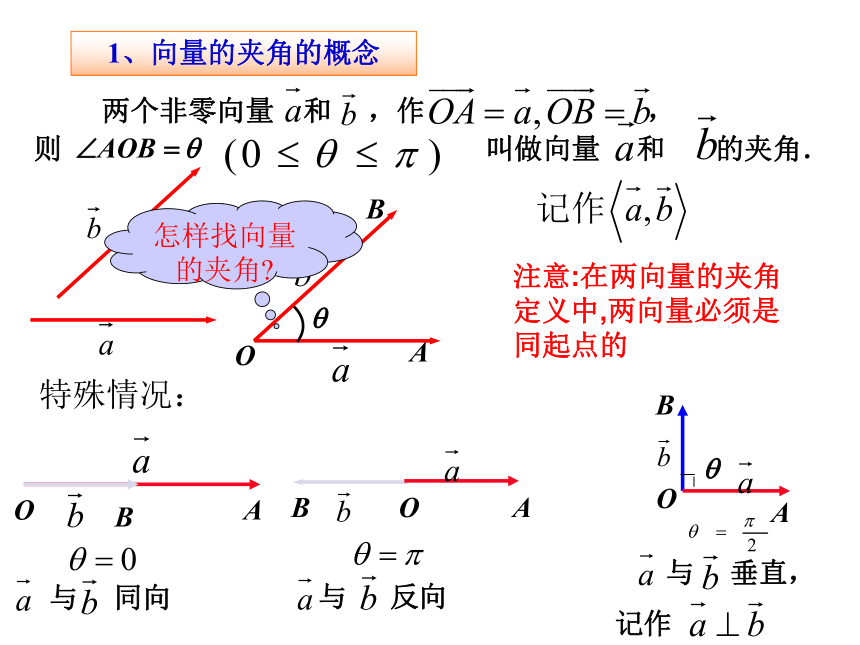
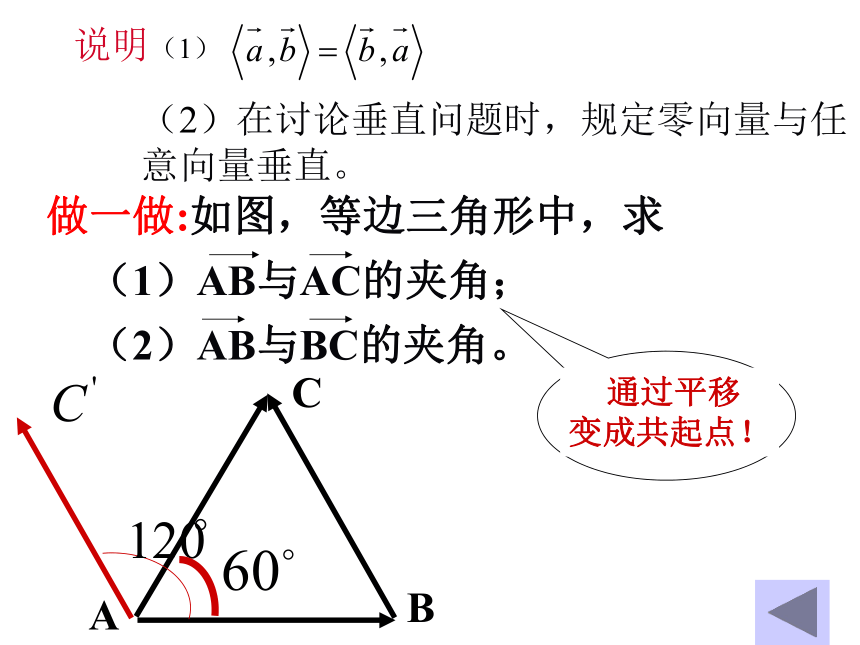
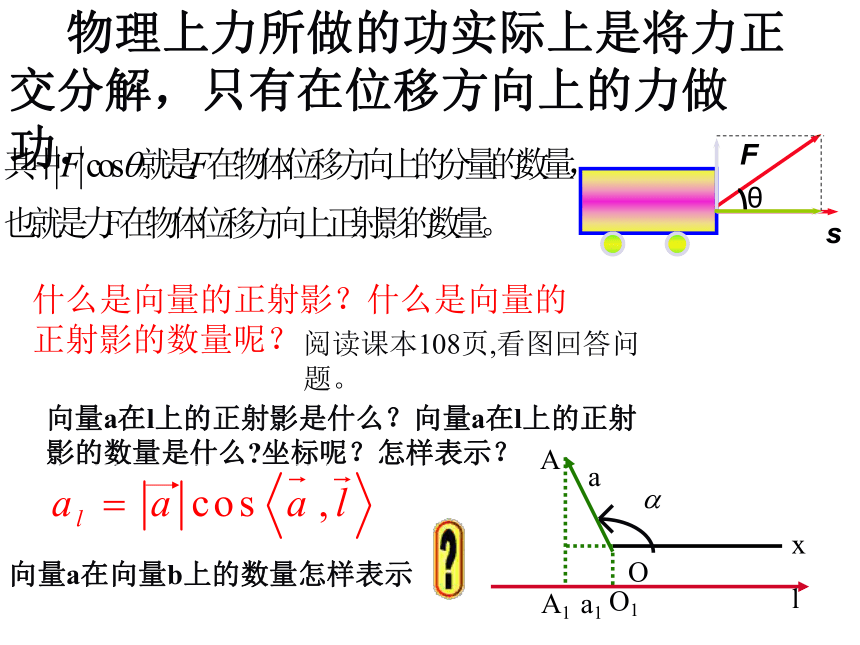
以计算力做功为背景,我们引入向量的数量积的概念。力做功的计算,涉及到两个概念: 两个向量的夹角向量在轴上的射影1、向量的夹角的概念记作注意:在两向量的夹角定义中,两向量必须是同起点的特殊情况:怎样找向量的夹角?说明(1)(2)在讨论垂直问题时,规定零向量与任意向量垂直。 物理上力所做的功实际上是将力正 交分解,只有在位移方向上的力做功.什么是向量的正射影?什么是向量的正射影的数量呢?阅读课本108页,看图回答问题。向量a在l上的正射影是什么?向量a在l上的正射影的数量是什么?坐标呢?怎样表示?练一练3、向量的数量积的定义说明判断下列命题是否正确(×)(×)(×)(×)做一做1.若a=0,则对任意向量b,有a ·b=0.
2.若a≠0,则对任意非零向量b,有a ·b≠0.
3.若a≠0,且a · b=0,则b=0.
4.若a·b=0,则a=0或b=0.
5.对任意的向量a,有a2=│a│2.
6.若a≠0,且a · b=a · c,则b=c.(×) 小组讨论结论θ为锐角时,
| b | cos >0θ为直角时,
| b | cos =0θ为钝角时,
| b | cos <0当夹角为 和180° ,结果是什么呢?平面向量数量积 a · b的几何意义 向量 a 与b 的数量积等于a 的长度 |a| 与b 在a 的方向上的正射影的数量| b | cosθ的积.还有其它说法吗?过A点作OB的垂线,其几何意义怎样表述呢?想一想:由向量数量积的定义,试完成下面问题:0≤(4)练一练:3、向量数量积的性质例题讲解例1.已知|a |=5,|b |=4, ,求a ·b.解:例2 已知a=(1,1),b=(2,0),求a·b。
解: |a| =√2, |b|=2, θ=45 °
∴ a·b=|a| |b|cosθ= √2×2×cos45 °
= 2看谁做的快答案:-28例3看谁做的快:练习A,2求向量夹角的方法求向量模的方法例4看谁做的快我们学到了什么?课堂小结向量的夹角向量在轴上的正射影向量的数量积的定义,几何意义,性质。共起点 向量 a 与b 的数量积等于a 的长度 |a| 与b 在a 的方向上的正射影的数量| b | cosθ的积.
数量积的
性
质
(1)e · a=a · e=| a | cos? (5)| a · b| ≤| a | · | b | 设a ,b都是非零向量, e是与b方向相同的单位向量,
? 是a与e的夹角,则(用于计算向量的夹角)
向量的加法
向量的减法
实数与向量的乘法
两个向量的数量积运算结果向量向量向量向量数量积的物理背景与定义学习目标 1、掌握平面向量数量积的物理
背景; 3、掌握平面向量数量积的定义性质及几何意义。 2、理解一个向量在另一个向量
方向上的正投影的概念; 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)
W=|F| |S|cosθ 其中θ是F与S的夹角新课引入:功是一个标量,是一个数量,它由力和位移两个向量来确定。这给我们一种启示,能否把“功”看成这两个向量的一种运算的结果呢?力F所做的功W应当怎样计算?
以计算力做功为背景,我们引入向量的数量积的概念。力做功的计算,涉及到两个概念: 两个向量的夹角向量在轴上的射影1、向量的夹角的概念记作注意:在两向量的夹角定义中,两向量必须是同起点的特殊情况:怎样找向量的夹角?说明(1)(2)在讨论垂直问题时,规定零向量与任意向量垂直。 物理上力所做的功实际上是将力正 交分解,只有在位移方向上的力做功.什么是向量的正射影?什么是向量的正射影的数量呢?阅读课本108页,看图回答问题。向量a在l上的正射影是什么?向量a在l上的正射影的数量是什么?坐标呢?怎样表示?练一练3、向量的数量积的定义说明判断下列命题是否正确(×)(×)(×)(×)做一做1.若a=0,则对任意向量b,有a ·b=0.
2.若a≠0,则对任意非零向量b,有a ·b≠0.
3.若a≠0,且a · b=0,则b=0.
4.若a·b=0,则a=0或b=0.
5.对任意的向量a,有a2=│a│2.
6.若a≠0,且a · b=a · c,则b=c.(×) 小组讨论结论θ为锐角时,
| b | cos >0θ为直角时,
| b | cos =0θ为钝角时,
| b | cos <0当夹角为 和180° ,结果是什么呢?平面向量数量积 a · b的几何意义 向量 a 与b 的数量积等于a 的长度 |a| 与b 在a 的方向上的正射影的数量| b | cosθ的积.还有其它说法吗?过A点作OB的垂线,其几何意义怎样表述呢?想一想:由向量数量积的定义,试完成下面问题:0≤(4)练一练:3、向量数量积的性质例题讲解例1.已知|a |=5,|b |=4, ,求a ·b.解:例2 已知a=(1,1),b=(2,0),求a·b。
解: |a| =√2, |b|=2, θ=45 °
∴ a·b=|a| |b|cosθ= √2×2×cos45 °
= 2看谁做的快答案:-28例3看谁做的快:练习A,2求向量夹角的方法求向量模的方法例4看谁做的快我们学到了什么?课堂小结向量的夹角向量在轴上的正射影向量的数量积的定义,几何意义,性质。共起点 向量 a 与b 的数量积等于a 的长度 |a| 与b 在a 的方向上的正射影的数量| b | cosθ的积.
数量积的
性
质
(1)e · a=a · e=| a | cos? (5)| a · b| ≤| a | · | b | 设a ,b都是非零向量, e是与b方向相同的单位向量,
? 是a与e的夹角,则(用于计算向量的夹角)
