数学:3.2.1《几类不同增长的函数模型》课件(新人教a版必修1)
文档属性
| 名称 | 数学:3.2.1《几类不同增长的函数模型》课件(新人教a版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览





文档简介
课件22张PPT。几种不同增长的函数模型2019-3-13例1、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前
一天多回报10元;方案三:第一天回报0.4元,以后每天的回
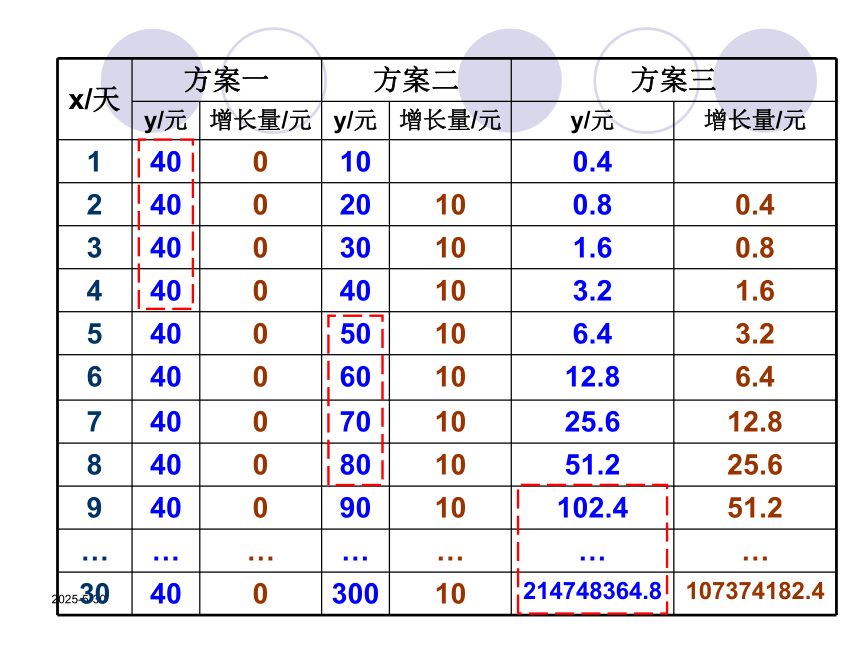
报比前 一天翻一番。请问,你会选择哪种投资方案呢?2019-3-13思考 比较三种方案每天回报量
(2) 比较三种方案一段时间内的总回报量 哪个方案在某段时间内的总回报量最多,我们就在那段时间选择该方案。2019-3-13分析 我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据。解:设第x天所得回报为y元,则
方案一:每天回报40元; y=40 (x∈N*)方案二:第一天回报10元,以后每天比前一天多回 报10元; y=10x (x∈N*)方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
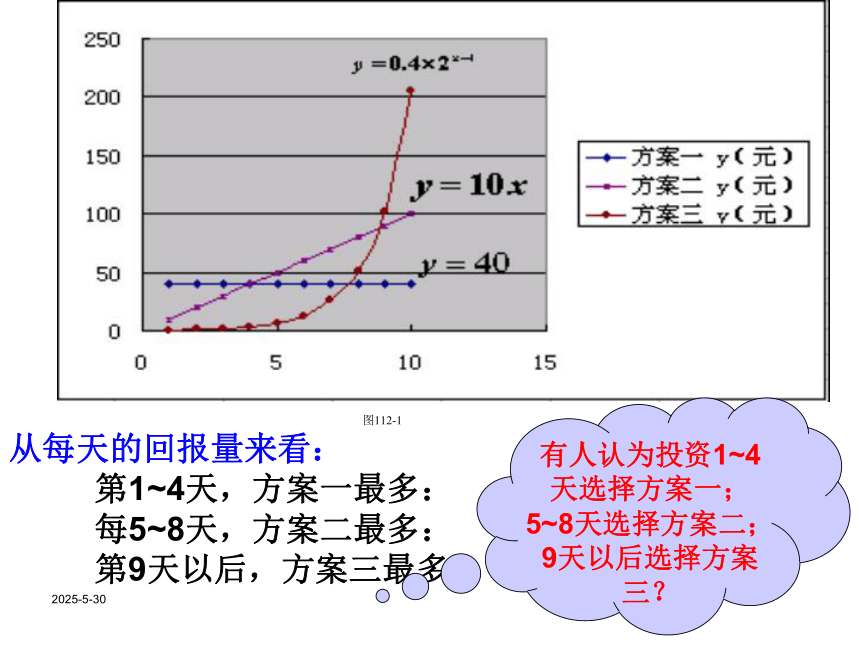
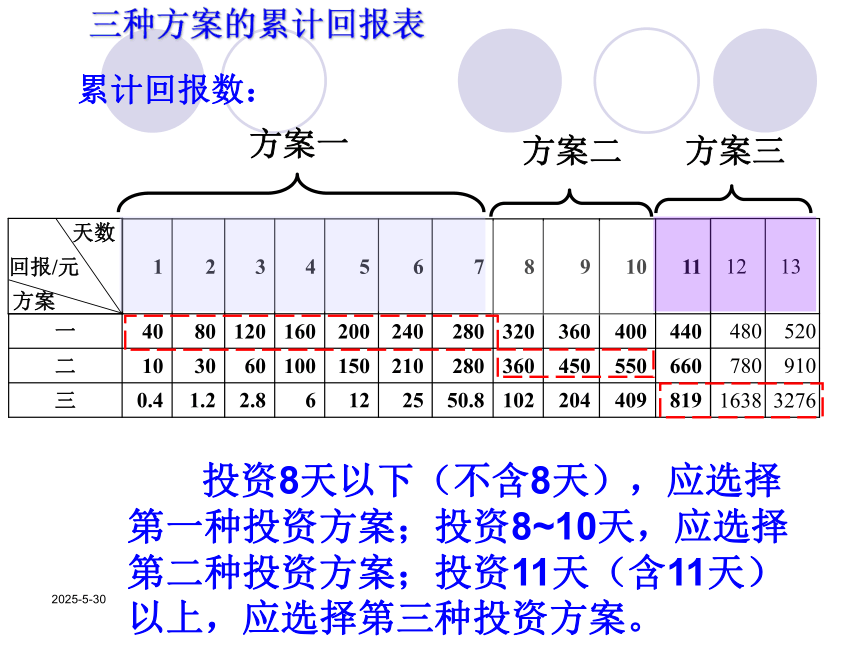
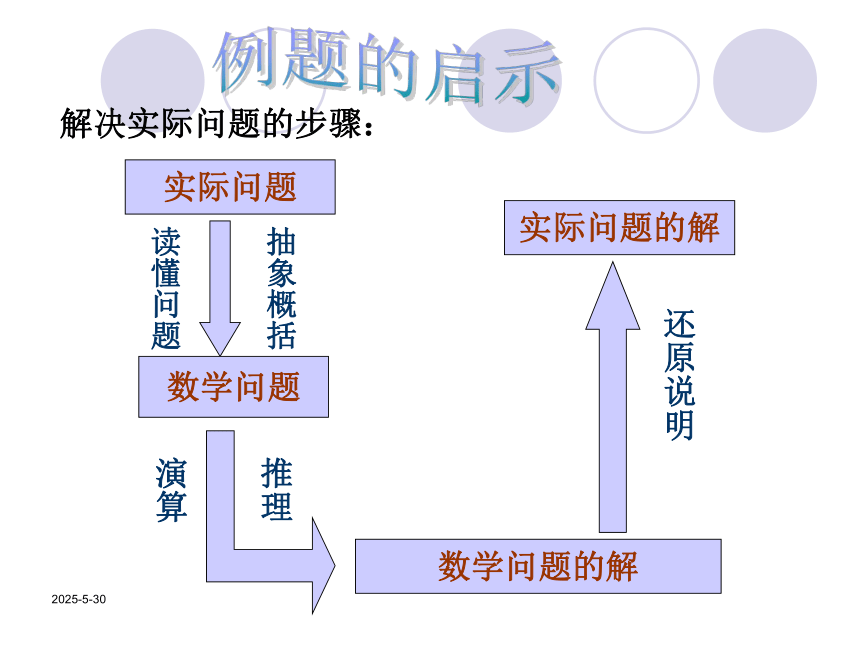
y=0.4×2x-1 (x∈N*)2019-3-132019-3-13从每天的回报量来看: 第1~4天,方案一最多: 每5~8天,方案二最多: 第9天以后,方案三最多;有人认为投资1~4天选择方案一;5~8天选择方案二;9天以后选择方案三?2019-3-13 三种方案的累计回报表 投资8天以下(不含8天),应选择第一种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。2019-3-13例题的启示解决实际问题的步骤:实际问题读懂问题抽象概括数学问题演算推理数学问题的解还原说明实际问题的解2019-3-13例2、某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?2019-3-132019-3-13(1)、由函数图象可以看出,
它在区间[10,1000]上递增,
而且当x=1000时,
y=log71000+1≈4.55<5,所
以它符合资金不超过5万元的要求。模型y=log7x+12019-3-13令f(x)= log7x+1-0.25x, x∈ [10,1000].利用计算机作出函数f(x)的图象,由图象可知它是递减的,因此 f(x)即 log7x+1<0.25x2019-3-13思考从上节课的两个例子中可以看到,这三类
函数的增长是有差异的,那么,这种差异
的具体情况到底怎么样呢?2019-3-132019-3-132019-3-13结论1:一般地,对于指数函数
y=ax (a>1)和幂函数y=xn (n>0),通过探索可以发现:在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.2019-3-13结论2:一般地,对于对数函数y=logax (a>1)和幂函数y=xn (n>0),通过探索可以发现:在区间(0,+∞)上,随着x的增大,logax增大得越来越慢,图象就像是渐渐地与x轴平行一样。尽管在x的一定变化范围内, logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax1),y=logax (a>1)和y=xn (n>0)都是增函数。(2)、随着x的增大, y=ax (a>1)的增长速度越来越快,会远远大于y=xn (n>0)的增长速度。(3)、随着x的增大, y=logax (a>1)的增长速度越来越慢,会远远小于y=xn (n>0)的增长速度。总存在一个x0,当x>x0时,就有
logaxy=x2+7和y=2x的图象
如图.试比较x2+7与2x的
大小.5040302010510y=x2+7y=2xxyO2019-3-13例2 已知函数y=x2和y=log2(x+1)的图象
如图,试比较x2与log2(x+1)的大小.4321-124xyOy=x2y=log2(x+1)2019-3-13 1.复习课本p95-1013.继续完成课本p101练习.
(做在书上或课堂练习本上)课后作业2.完成课本p82复习参考题A组10及B组5,6(做在作业本上)4.预习课本p101-106试做p106练习1,2.)5.三维创新p74-77§3.2第一课时2019-3-132019-3-13
一天多回报10元;方案三:第一天回报0.4元,以后每天的回
报比前 一天翻一番。请问,你会选择哪种投资方案呢?2019-3-13思考 比较三种方案每天回报量
(2) 比较三种方案一段时间内的总回报量 哪个方案在某段时间内的总回报量最多,我们就在那段时间选择该方案。2019-3-13分析 我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据。解:设第x天所得回报为y元,则
方案一:每天回报40元; y=40 (x∈N*)方案二:第一天回报10元,以后每天比前一天多回 报10元; y=10x (x∈N*)方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
y=0.4×2x-1 (x∈N*)2019-3-132019-3-13从每天的回报量来看: 第1~4天,方案一最多: 每5~8天,方案二最多: 第9天以后,方案三最多;有人认为投资1~4天选择方案一;5~8天选择方案二;9天以后选择方案三?2019-3-13 三种方案的累计回报表 投资8天以下(不含8天),应选择第一种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。2019-3-13例题的启示解决实际问题的步骤:实际问题读懂问题抽象概括数学问题演算推理数学问题的解还原说明实际问题的解2019-3-13例2、某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?2019-3-132019-3-13(1)、由函数图象可以看出,
它在区间[10,1000]上递增,
而且当x=1000时,
y=log71000+1≈4.55<5,所
以它符合资金不超过5万元的要求。模型y=log7x+12019-3-13令f(x)= log7x+1-0.25x, x∈ [10,1000].利用计算机作出函数f(x)的图象,由图象可知它是递减的,因此 f(x)
函数的增长是有差异的,那么,这种差异
的具体情况到底怎么样呢?2019-3-132019-3-132019-3-13结论1:一般地,对于指数函数
y=ax (a>1)和幂函数y=xn (n>0),通过探索可以发现:在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.2019-3-13结论2:一般地,对于对数函数y=logax (a>1)和幂函数y=xn (n>0),通过探索可以发现:在区间(0,+∞)上,随着x的增大,logax增大得越来越慢,图象就像是渐渐地与x轴平行一样。尽管在x的一定变化范围内, logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax
logax
如图.试比较x2+7与2x的
大小.5040302010510y=x2+7y=2xxyO2019-3-13例2 已知函数y=x2和y=log2(x+1)的图象
如图,试比较x2与log2(x+1)的大小.4321-124xyOy=x2y=log2(x+1)2019-3-13 1.复习课本p95-1013.继续完成课本p101练习.
(做在书上或课堂练习本上)课后作业2.完成课本p82复习参考题A组10及B组5,6(做在作业本上)4.预习课本p101-106试做p106练习1,2.)5.三维创新p74-77§3.2第一课时2019-3-132019-3-13
