浙江省中考数学考前冲刺每日一练41(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练41(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 403.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 16:03:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练41(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.为了解某地某天的天气情况,在某气象网站查询到该地这天的最低气温为﹣2℃,最高气温为7℃.则该地这天的温差(最高气温与最低气温的差)为( )
A.﹣9℃ B.﹣5℃ C.5℃ D.9℃
2.请写出一个小于3的无理数 .
3.如图,一次函数y=x+1的图象与反比例函数y=(k≠0)的图象交于点A(a,3),与y轴交于点B.
(1)求点A的坐标和反比例函数的表达式;
(2)若点P在y轴上,△ABP的面积为6,求点P的坐标.
4.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
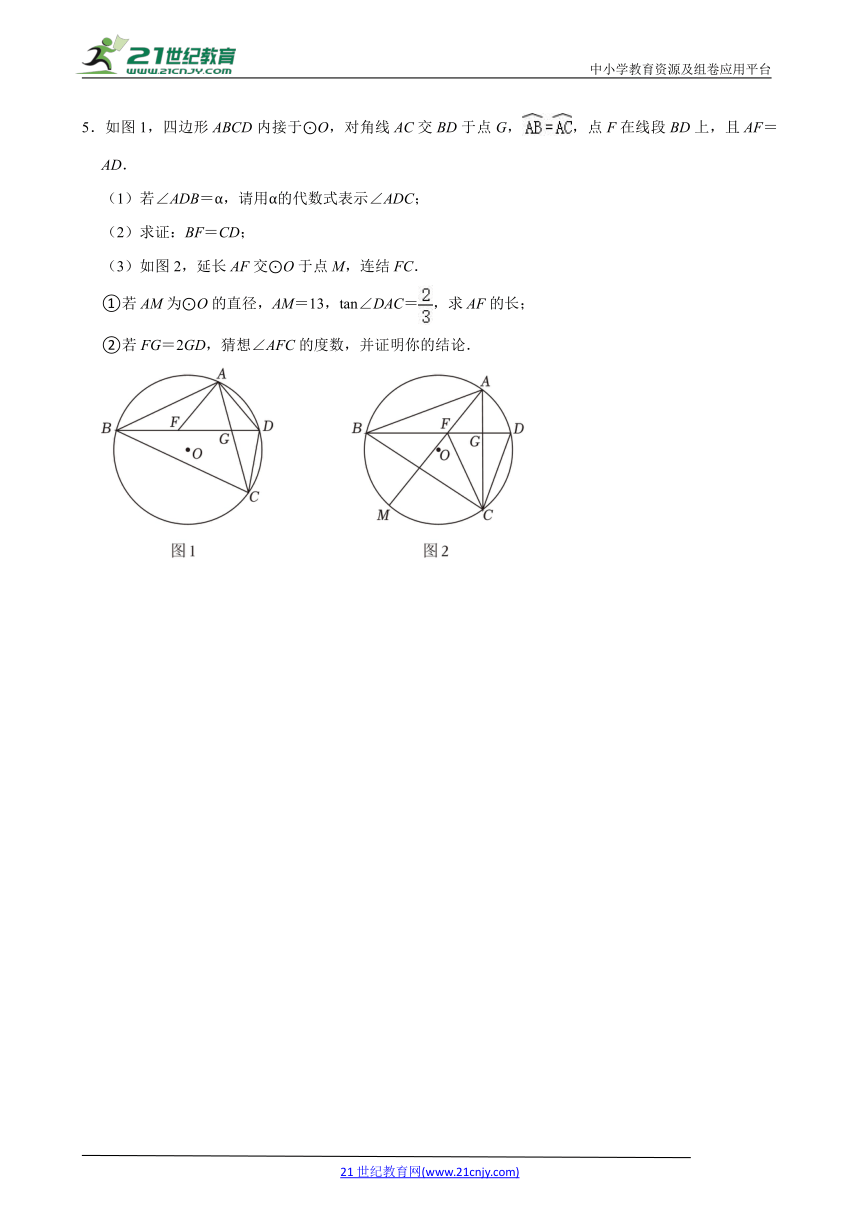
5.如图1,四边形ABCD内接于⊙O,对角线AC交BD于点G,,点F在线段BD上,且AF=AD.
(1)若∠ADB=α,请用α的代数式表示∠ADC;
(2)求证:BF=CD;
(3)如图2,延长AF交⊙O于点M,连结FC.
①若AM为⊙O的直径,AM=13,tan∠DAC=,求AF的长;
②若FG=2GD,猜想∠AFC的度数,并证明你的结论.
浙江省中考数学考前冲刺每日一练41(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
参考答案与试题解析
一.选择题(共1小题)
1.为了解某地某天的天气情况,在某气象网站查询到该地这天的最低气温为﹣2℃,最高气温为7℃.则该地这天的温差(最高气温与最低气温的差)为( )
A.﹣9℃ B.﹣5℃ C.5℃ D.9℃
【分析】根据题意列出式子再进行计算即可.
【解答】解:7﹣(﹣2)=9(℃).
故选:D.
【点评】本题考查有理数的减法,熟练掌握相关的知识点是解题的关键.
二.填空题(共1小题)
2.请写出一个小于3的无理数 .
【分析】符合题意的无理数既可以.
【解答】解:小于3的无理数无限多个.例如:、、、、2.1010010001...(两个1之间依次多一个0)等.
故答案为:.
【点评】本题考查了无理数,掌握无理数的定义,会比较无理数的大小是解决本题的关键.
三.解答题(共3小题)
3.如图1,四边形ABCD内接于⊙O,对角线AC交BD于点G,,点F在线段BD上,且AF=AD.
(1)若∠ADB=α,请用α的代数式表示∠ADC;
(2)求证:BF=CD;
(3)如图2,延长AF交⊙O于点M,连结FC.
①若AM为⊙O的直径,AM=13,tan∠DAC=,求AF的长;
②若FG=2GD,猜想∠AFC的度数,并证明你的结论.
【分析】(1)根据等弧所对的圆周角相等得∠ABC=∠ADB=α,再由圆内接四边形的性质可得结论.
(2)分别证明∠AFB=∠ADC,∠ABD=∠ACD,再证明△ABF≌△ACD(AAS)即可得到结论.
(3)①连接BM,MC,Rt△ABM≌Rt△ACM(HL),得∠DAC=∠BAM=∠CAM=∠CBM,tan∠DAC=,得,,求得BP=6,MP=4,AP=9,即可求得AF的长.②连接BM,CM,过点F作FQ∥BM交MC于点Q,证明△ADG∽△BFP,△AFG∽△BMP,得,,求得MP=2PF,证明△BFP∽△CMP,四边形BMQF是平行四边形,可得四边形BMQF是菱形,进一步可求得结论.
【解答】(1)解:∵.
∴∠ABC=∠ADB=α.
∵四边形ABCD内接于⊙O.
∴∠ABC+∠ADC=180°.
∴∠ADC=180°﹣∠ABC=180°﹣α.
(2)证明:∵AF=AD.
∴∠AFD=∠ADB=α.
∴∠AFB=180°﹣∠AFD=180°﹣α.
∴∠AFB=∠ADC.
∵∠ABD,∠ACD是所对的圆周角.
∴∠ABD=∠ACD.
又AF=AD.
∴△ABF≌△ACD(AAS).
∴BF=CD.
(3)①解:如图2,连接BM,MC.
.
∵AM是直径.
∴∠ABM=∠ACM=90°.
∵△ABF≌△ACD(AAS).
∴∠BAM=∠CAD,AB=AC.
又AM=AM.
∴Rt△ABM≌Rt△ACM(HL).
∴BM=CM,∠BAM=∠CAM.
∴∠DAC=∠BAM=∠CAM=∠CBM.
∵AB=AC.
∴AM⊥BC且AM平分BC.
∵tan∠DAC=,AM=13.
∴,.
∴BP=6,MP=4,AP=9.
∴PF=MP=4.
∴AF=AP﹣PF=9﹣4=5.
②猜想:∠AFC=90°.
如图,连接BM,CM,过点F作FQ∥BM交MC于点Q.
.
∵AB=AC,AF=AD.
∴∠1=∠2=∠4=∠5=∠7.
∵∠3,∠6是所对的圆周角.
∴∠3=∠6.
∴△ADG∽△BFP,△AFG∽△BMP.
∴,.
∵FG=2GD.
∴MP=2PF.
∵∠2=∠7.
∴BD∥MC.
∴△BFP∽△CMP,四边形BMQF是平行四边形.
∴.
∵∠4=∠5.
∴BM=BF.
∴四边形BMQF是菱形.
∴BF=MQ=FQ.
∴MQ=FQ=QC.
∴∠7=∠MFQ,∠MCF=∠QFC.
∵∠7+∠MFQ+∠MCF+∠QFC=180°.
∴∠MFC=90°.
∴∠AFC=90°.
【点评】本题主要考查了圆内接四边形,圆周角定理,全等三角形的判定与性质,平行四边形的判定与性质,菱形的判定与性质,相似三角形的判定与性质,锐角三角函数的意义等知识,正确作出辅助线是解答本题的关键.
4.如图,一次函数y=x+1的图象与反比例函数y=(k≠0)的图象交于点A(a,3),与y轴交于点B.
(1)求点A的坐标和反比例函数的表达式;
(2)若点P在y轴上,△ABP的面积为6,求点P的坐标.
【分析】(1)将点A的坐标代入一次函数表达式,求出a=4,即可求得A的坐标,将点A的坐标代入反比例函数表达式,求出k即可;
(2)利用右侧函数的不等式求得点B的坐标,然后根据三角形面积公式求得BP,即可求得P点的坐标.
【解答】解:(1)将点A(a,3)代入y=x+1,
得:3=a+1,
解得:a=4,
则点A(4,3),
将点A的坐标代入反比例函数表达式得:3=,
解得:k=12,
∴反比例函数的表达式为y=;
(2)∵一次函数y=x+1的图象与y轴交于点B,
∴B(0,1),
∵点P在y轴上,△ABP的面积为6,
∴=6,即,
∴BP=3,
∴点P的坐标为(0,4)或(0,﹣2).
【点评】本题考查了利用待定系数法求反比例函数,函数图象上点的坐标特征,三角形的面积,属于基础知识,需熟练掌握.
5.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
【分析】(1)依据题意,求出Δ=b2﹣4a(﹣4a)=b2+16a2,进而结合a≠0可以判断Δ>0,即可求解;
(2)依据题意,也有对称轴为直线x=2,可得b=﹣4a,从而y=ax2+bx﹣4a=ax2﹣4ax﹣4a,当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,然后计算即可求解;
(3)依据题意,由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,则抛物线开口向下,即a<0,进而求解.
【解答】解:(1)由题意得,Δ=b2﹣4a(﹣4a)=b2+16a2,
又a≠0,
∴a2>0.
∴16a2>0.
又对于任意的b都有b2≥0,
∴Δ=b2+16a2>0.
∴函数图象与x轴的交点个数为2.
(2)∵x=2=﹣,
∴b=﹣4a.
∴抛物线表达式为y=ax2+bx﹣4a=ax2﹣4ax﹣4a,
当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,
解得x=6或﹣2,
则x1=﹣2,x2=6.
(3)将(1,2)代入抛物线表达式得:2=a+b﹣4a,则b=3a+2,
∵a<b,故a<3a+2,
∴解得a>﹣1.
∴抛物线的表达式为y=ax2+(3a+2)x﹣4a,
由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,
∴抛物线开口向下,即a<0.
∴函数的对称轴x=﹣=﹣﹣<0,
解得a<﹣,
∴﹣1<a<﹣.
∴﹣3<3a<﹣2.
故﹣1<3a+2<0,即﹣1<b<0.
∴﹣4<3a+b<﹣2.
∴3a+b的取值范围:﹣4<3a+b<﹣2.
【点评】本题主要考查的是抛物线与x轴的交点、函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练41(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.为了解某地某天的天气情况,在某气象网站查询到该地这天的最低气温为﹣2℃,最高气温为7℃.则该地这天的温差(最高气温与最低气温的差)为( )
A.﹣9℃ B.﹣5℃ C.5℃ D.9℃
2.请写出一个小于3的无理数 .
3.如图,一次函数y=x+1的图象与反比例函数y=(k≠0)的图象交于点A(a,3),与y轴交于点B.
(1)求点A的坐标和反比例函数的表达式;
(2)若点P在y轴上,△ABP的面积为6,求点P的坐标.
4.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
5.如图1,四边形ABCD内接于⊙O,对角线AC交BD于点G,,点F在线段BD上,且AF=AD.
(1)若∠ADB=α,请用α的代数式表示∠ADC;
(2)求证:BF=CD;
(3)如图2,延长AF交⊙O于点M,连结FC.
①若AM为⊙O的直径,AM=13,tan∠DAC=,求AF的长;
②若FG=2GD,猜想∠AFC的度数,并证明你的结论.
浙江省中考数学考前冲刺每日一练41(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
参考答案与试题解析
一.选择题(共1小题)
1.为了解某地某天的天气情况,在某气象网站查询到该地这天的最低气温为﹣2℃,最高气温为7℃.则该地这天的温差(最高气温与最低气温的差)为( )
A.﹣9℃ B.﹣5℃ C.5℃ D.9℃
【分析】根据题意列出式子再进行计算即可.
【解答】解:7﹣(﹣2)=9(℃).
故选:D.
【点评】本题考查有理数的减法,熟练掌握相关的知识点是解题的关键.
二.填空题(共1小题)
2.请写出一个小于3的无理数 .
【分析】符合题意的无理数既可以.
【解答】解:小于3的无理数无限多个.例如:、、、、2.1010010001...(两个1之间依次多一个0)等.
故答案为:.
【点评】本题考查了无理数,掌握无理数的定义,会比较无理数的大小是解决本题的关键.
三.解答题(共3小题)
3.如图1,四边形ABCD内接于⊙O,对角线AC交BD于点G,,点F在线段BD上,且AF=AD.
(1)若∠ADB=α,请用α的代数式表示∠ADC;
(2)求证:BF=CD;
(3)如图2,延长AF交⊙O于点M,连结FC.
①若AM为⊙O的直径,AM=13,tan∠DAC=,求AF的长;
②若FG=2GD,猜想∠AFC的度数,并证明你的结论.
【分析】(1)根据等弧所对的圆周角相等得∠ABC=∠ADB=α,再由圆内接四边形的性质可得结论.
(2)分别证明∠AFB=∠ADC,∠ABD=∠ACD,再证明△ABF≌△ACD(AAS)即可得到结论.
(3)①连接BM,MC,Rt△ABM≌Rt△ACM(HL),得∠DAC=∠BAM=∠CAM=∠CBM,tan∠DAC=,得,,求得BP=6,MP=4,AP=9,即可求得AF的长.②连接BM,CM,过点F作FQ∥BM交MC于点Q,证明△ADG∽△BFP,△AFG∽△BMP,得,,求得MP=2PF,证明△BFP∽△CMP,四边形BMQF是平行四边形,可得四边形BMQF是菱形,进一步可求得结论.
【解答】(1)解:∵.
∴∠ABC=∠ADB=α.
∵四边形ABCD内接于⊙O.
∴∠ABC+∠ADC=180°.
∴∠ADC=180°﹣∠ABC=180°﹣α.
(2)证明:∵AF=AD.
∴∠AFD=∠ADB=α.
∴∠AFB=180°﹣∠AFD=180°﹣α.
∴∠AFB=∠ADC.
∵∠ABD,∠ACD是所对的圆周角.
∴∠ABD=∠ACD.
又AF=AD.
∴△ABF≌△ACD(AAS).
∴BF=CD.
(3)①解:如图2,连接BM,MC.
.
∵AM是直径.
∴∠ABM=∠ACM=90°.
∵△ABF≌△ACD(AAS).
∴∠BAM=∠CAD,AB=AC.
又AM=AM.
∴Rt△ABM≌Rt△ACM(HL).
∴BM=CM,∠BAM=∠CAM.
∴∠DAC=∠BAM=∠CAM=∠CBM.
∵AB=AC.
∴AM⊥BC且AM平分BC.
∵tan∠DAC=,AM=13.
∴,.
∴BP=6,MP=4,AP=9.
∴PF=MP=4.
∴AF=AP﹣PF=9﹣4=5.
②猜想:∠AFC=90°.
如图,连接BM,CM,过点F作FQ∥BM交MC于点Q.
.
∵AB=AC,AF=AD.
∴∠1=∠2=∠4=∠5=∠7.
∵∠3,∠6是所对的圆周角.
∴∠3=∠6.
∴△ADG∽△BFP,△AFG∽△BMP.
∴,.
∵FG=2GD.
∴MP=2PF.
∵∠2=∠7.
∴BD∥MC.
∴△BFP∽△CMP,四边形BMQF是平行四边形.
∴.
∵∠4=∠5.
∴BM=BF.
∴四边形BMQF是菱形.
∴BF=MQ=FQ.
∴MQ=FQ=QC.
∴∠7=∠MFQ,∠MCF=∠QFC.
∵∠7+∠MFQ+∠MCF+∠QFC=180°.
∴∠MFC=90°.
∴∠AFC=90°.
【点评】本题主要考查了圆内接四边形,圆周角定理,全等三角形的判定与性质,平行四边形的判定与性质,菱形的判定与性质,相似三角形的判定与性质,锐角三角函数的意义等知识,正确作出辅助线是解答本题的关键.
4.如图,一次函数y=x+1的图象与反比例函数y=(k≠0)的图象交于点A(a,3),与y轴交于点B.
(1)求点A的坐标和反比例函数的表达式;
(2)若点P在y轴上,△ABP的面积为6,求点P的坐标.
【分析】(1)将点A的坐标代入一次函数表达式,求出a=4,即可求得A的坐标,将点A的坐标代入反比例函数表达式,求出k即可;
(2)利用右侧函数的不等式求得点B的坐标,然后根据三角形面积公式求得BP,即可求得P点的坐标.
【解答】解:(1)将点A(a,3)代入y=x+1,
得:3=a+1,
解得:a=4,
则点A(4,3),
将点A的坐标代入反比例函数表达式得:3=,
解得:k=12,
∴反比例函数的表达式为y=;
(2)∵一次函数y=x+1的图象与y轴交于点B,
∴B(0,1),
∵点P在y轴上,△ABP的面积为6,
∴=6,即,
∴BP=3,
∴点P的坐标为(0,4)或(0,﹣2).
【点评】本题考查了利用待定系数法求反比例函数,函数图象上点的坐标特征,三角形的面积,属于基础知识,需熟练掌握.
5.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
【分析】(1)依据题意,求出Δ=b2﹣4a(﹣4a)=b2+16a2,进而结合a≠0可以判断Δ>0,即可求解;
(2)依据题意,也有对称轴为直线x=2,可得b=﹣4a,从而y=ax2+bx﹣4a=ax2﹣4ax﹣4a,当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,然后计算即可求解;
(3)依据题意,由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,则抛物线开口向下,即a<0,进而求解.
【解答】解:(1)由题意得,Δ=b2﹣4a(﹣4a)=b2+16a2,
又a≠0,
∴a2>0.
∴16a2>0.
又对于任意的b都有b2≥0,
∴Δ=b2+16a2>0.
∴函数图象与x轴的交点个数为2.
(2)∵x=2=﹣,
∴b=﹣4a.
∴抛物线表达式为y=ax2+bx﹣4a=ax2﹣4ax﹣4a,
当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,
解得x=6或﹣2,
则x1=﹣2,x2=6.
(3)将(1,2)代入抛物线表达式得:2=a+b﹣4a,则b=3a+2,
∵a<b,故a<3a+2,
∴解得a>﹣1.
∴抛物线的表达式为y=ax2+(3a+2)x﹣4a,
由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,
∴抛物线开口向下,即a<0.
∴函数的对称轴x=﹣=﹣﹣<0,
解得a<﹣,
∴﹣1<a<﹣.
∴﹣3<3a<﹣2.
故﹣1<3a+2<0,即﹣1<b<0.
∴﹣4<3a+b<﹣2.
∴3a+b的取值范围:﹣4<3a+b<﹣2.
【点评】本题主要考查的是抛物线与x轴的交点、函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
