浙江省中考数学考前冲刺每日一练43(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练43(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |

|
|
| 格式 | doc | ||
| 文件大小 | 253.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练43(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
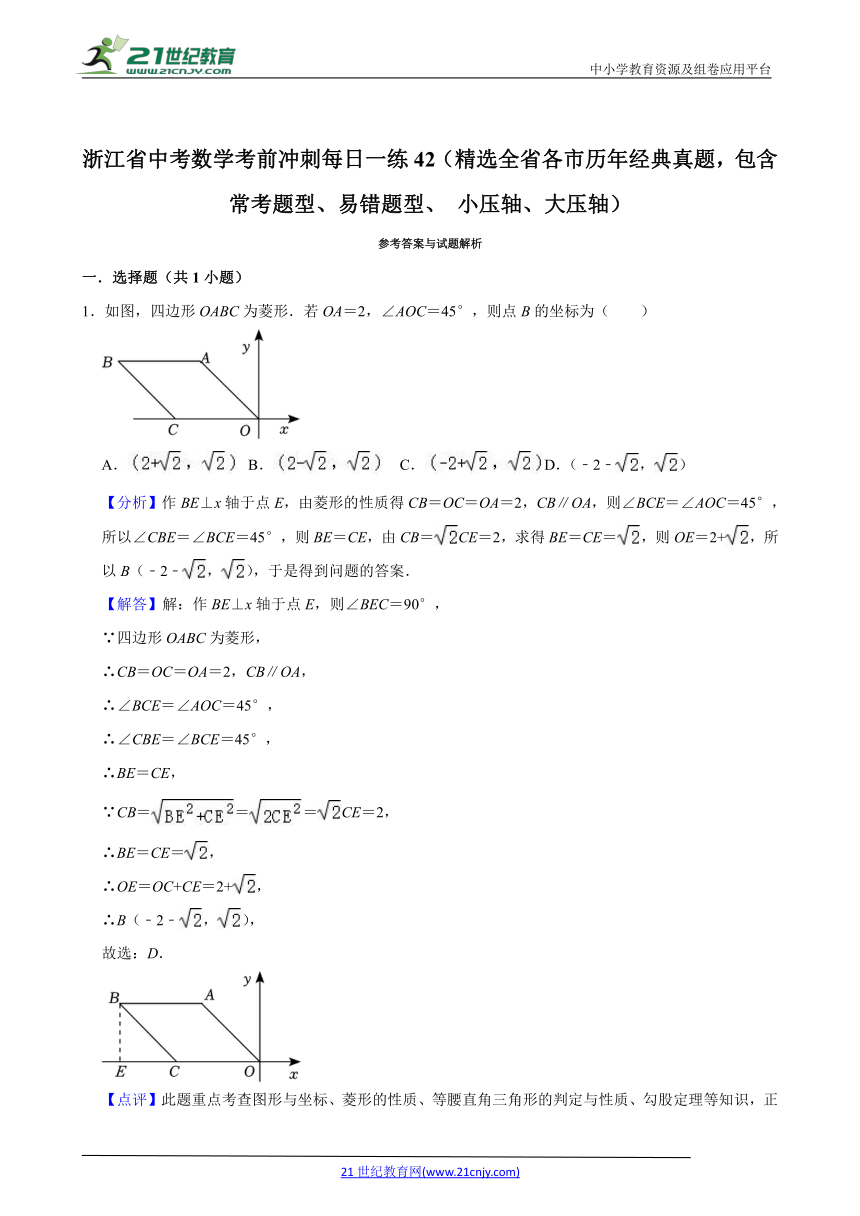
1.如图,四边形OABC为菱形.若OA=2,∠AOC=45°,则点B的坐标为( )
A. B. C. D.(﹣2﹣,)
2.在一个不透明的布袋中装有黄、白两种颜色的球,除颜色外其他都相同.从袋中随机取出一个球是黄球的概率为0.4,若袋中有12个白球,则布袋中黄球可能有 个.
3.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 .
4.综合与实践:如何称量一个空矿泉水瓶的重量?
素材1:如图是一架自制天平,支点O固定不变,左侧托盘固定在点A处,右侧托盘的点P可以在横梁BC段滑动.已知OA=OC=12cm,BC=28cm,一个100g的砝码.
素材2:由于一个空的矿泉水瓶太轻无法称量,小组进行如下操作:左侧托盘放置砝码,右侧托盘滑动点P至点B,空瓶中加入适量的水使天平平衡,再向瓶中加入等量的水,发现点P移动到PC长12cm时,天平平衡.
链接:根据杠杆原理,平衡时:左盘砝码重量×OA=右盘物体重量×OP.(不计托盘与横梁重量)
任务1:设右侧托盘放置y(g)物体,OP长x(cm),求y关于x的函数表达式,并求出y的取值范围.
任务2:求这个空矿泉水瓶的重量.
5.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
参考答案与试题解析
一.选择题(共1小题)
1.如图,四边形OABC为菱形.若OA=2,∠AOC=45°,则点B的坐标为( )
A. B. C. D.(﹣2﹣,)
【分析】作BE⊥x轴于点E,由菱形的性质得CB=OC=OA=2,CB∥OA,则∠BCE=∠AOC=45°,所以∠CBE=∠BCE=45°,则BE=CE,由CB=CE=2,求得BE=CE=,则OE=2+,所以B(﹣2﹣,),于是得到问题的答案.
【解答】解:作BE⊥x轴于点E,则∠BEC=90°,
∵四边形OABC为菱形,
∴CB=OC=OA=2,CB∥OA,
∴∠BCE=∠AOC=45°,
∴∠CBE=∠BCE=45°,
∴BE=CE,
∵CB===CE=2,
∴BE=CE=,
∴OE=OC+CE=2+,
∴B(﹣2﹣,),
故选:D.
【点评】此题重点考查图形与坐标、菱形的性质、等腰直角三角形的判定与性质、勾股定理等知识,正确地作出辅助线是解题的关键.
二.填空题(共2小题)
2.在一个不透明的布袋中装有黄、白两种颜色的球,除颜色外其他都相同.从袋中随机取出一个球是黄球的概率为0.4,若袋中有12个白球,则布袋中黄球可能有 8 个.
【分析】布袋中黄球可能有x个,根据概率公式列出算式,再进行求解,即可得出答案.
【解答】解:布袋中黄球可能有x个,根据题意得:
=0.4,
解得:x=8,
经检验x=8是原方程的解,
答:布袋中黄球可能有8个.
故答案为:8.
【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率P(A)=.
3.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 ﹣6 .
【分析】依据题意,现将y=x2﹣2x+k变形为y=(x﹣1)2+k﹣1,然后结合﹣3≤x≤2判断当x=﹣3时取最大值,从而列方程计算可以得解.
【解答】解:由题意,∵y=x2﹣2x+k=x2﹣2x+1+k﹣1=(x﹣1)2+k﹣1,
∴抛物线的对称轴是直线x=1.
又∵﹣3≤x≤2,抛物线开口向上,
∴当x=﹣3时,y取最大值,最大值y=16+k﹣1=15+k.
又此时y的最大值为9,
∴15+k=9.
∴k=﹣6.
故答案为:﹣6.
【点评】本题主要考查了二次函数的性质,解题时要熟练掌握并能灵活运用顶点式是关键.
三.解答题(共2小题)
4.综合与实践:如何称量一个空矿泉水瓶的重量?
素材1:如图是一架自制天平,支点O固定不变,左侧托盘固定在点A处,右侧托盘的点P可以在横梁BC段滑动.已知OA=OC=12cm,BC=28cm,一个100g的砝码.
素材2:由于一个空的矿泉水瓶太轻无法称量,小组进行如下操作:左侧托盘放置砝码,右侧托盘滑动点P至点B,空瓶中加入适量的水使天平平衡,再向瓶中加入等量的水,发现点P移动到PC长12cm时,天平平衡.
链接:根据杠杆原理,平衡时:左盘砝码重量×OA=右盘物体重量×OP.(不计托盘与横梁重量)
任务1:设右侧托盘放置y(g)物体,OP长x(cm),求y关于x的函数表达式,并求出y的取值范围.
任务2:求这个空矿泉水瓶的重量.
【分析】任务1:根据左盘砝码重量×OA=右盘物体重量×OP,把相关数值代入后整理可得y与x的关系式,根据OP也就是x的取值范围可得y的取值范围;
任务2:设空瓶的质量为a g,两次加水的质量均为b g,根据左盘砝码重量×OA=右盘物体重量×OP列出二元一次方程组求解即可得到空瓶的质量.
【解答】解:任务1:∵左盘砝码重量×OA=右盘物体重量×OP,右侧托盘放置y(g)物体,OP长x(cm),砝码的质量是100g,OA=12cm,
∴100×12=xy.
∴y=.
∵OC=12cm,BC=28cm,
∴OB=40cm.
∵点P可以在横梁BC段滑动,
∴12≤OP≤40.
即12≤x≤40.
∴30≤y≤100.
答:y关于x的函数表达式为:y=(30≤y≤100);
任务2:设空瓶的重量为a g,两次加水的重量均为b g,根据题意,得:
.
解得:.
答:这个空矿泉水瓶的重量为10 g.
【点评】本题考查反比例函数的应用.根据杠杆平衡的条件找到相等关系并合理使用是解决本题的关键.
5.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
【分析】(1)依据题意,求出Δ=b2﹣4a(﹣4a)=b2+16a2,进而结合a≠0可以判断Δ>0,即可求解;
(2)依据题意,也有对称轴为直线x=2,可得b=﹣4a,从而y=ax2+bx﹣4a=ax2﹣4ax﹣4a,当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,然后计算即可求解;
(3)依据题意,由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,则抛物线开口向下,即a<0,进而求解.
【解答】解:(1)由题意得,Δ=b2﹣4a(﹣4a)=b2+16a2,
又a≠0,
∴a2>0.
∴16a2>0.
又对于任意的b都有b2≥0,
∴Δ=b2+16a2>0.
∴函数图象与x轴的交点个数为2.
(2)∵x=2=﹣,
∴b=﹣4a.
∴抛物线表达式为y=ax2+bx﹣4a=ax2﹣4ax﹣4a,
当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,
解得x=6或﹣2,
则x1=﹣2,x2=6.
(3)将(1,2)代入抛物线表达式得:2=a+b﹣4a,则b=3a+2,
∵a<b,故a<3a+2,
∴解得a>﹣1.
∴抛物线的表达式为y=ax2+(3a+2)x﹣4a,
由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,
∴抛物线开口向下,即a<0.
∴函数的对称轴x=﹣=﹣﹣<0,
解得a<﹣,
∴﹣1<a<﹣.
∴﹣3<3a<﹣2.
故﹣1<3a+2<0,即﹣1<b<0.
∴﹣4<3a+b<﹣2.
∴3a+b的取值范围:﹣4<3a+b<﹣2.
【点评】本题主要考查的是抛物线与x轴的交点、函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练43(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,四边形OABC为菱形.若OA=2,∠AOC=45°,则点B的坐标为( )
A. B. C. D.(﹣2﹣,)
2.在一个不透明的布袋中装有黄、白两种颜色的球,除颜色外其他都相同.从袋中随机取出一个球是黄球的概率为0.4,若袋中有12个白球,则布袋中黄球可能有 个.
3.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 .
4.综合与实践:如何称量一个空矿泉水瓶的重量?
素材1:如图是一架自制天平,支点O固定不变,左侧托盘固定在点A处,右侧托盘的点P可以在横梁BC段滑动.已知OA=OC=12cm,BC=28cm,一个100g的砝码.
素材2:由于一个空的矿泉水瓶太轻无法称量,小组进行如下操作:左侧托盘放置砝码,右侧托盘滑动点P至点B,空瓶中加入适量的水使天平平衡,再向瓶中加入等量的水,发现点P移动到PC长12cm时,天平平衡.
链接:根据杠杆原理,平衡时:左盘砝码重量×OA=右盘物体重量×OP.(不计托盘与横梁重量)
任务1:设右侧托盘放置y(g)物体,OP长x(cm),求y关于x的函数表达式,并求出y的取值范围.
任务2:求这个空矿泉水瓶的重量.
5.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
参考答案与试题解析
一.选择题(共1小题)
1.如图,四边形OABC为菱形.若OA=2,∠AOC=45°,则点B的坐标为( )
A. B. C. D.(﹣2﹣,)
【分析】作BE⊥x轴于点E,由菱形的性质得CB=OC=OA=2,CB∥OA,则∠BCE=∠AOC=45°,所以∠CBE=∠BCE=45°,则BE=CE,由CB=CE=2,求得BE=CE=,则OE=2+,所以B(﹣2﹣,),于是得到问题的答案.
【解答】解:作BE⊥x轴于点E,则∠BEC=90°,
∵四边形OABC为菱形,
∴CB=OC=OA=2,CB∥OA,
∴∠BCE=∠AOC=45°,
∴∠CBE=∠BCE=45°,
∴BE=CE,
∵CB===CE=2,
∴BE=CE=,
∴OE=OC+CE=2+,
∴B(﹣2﹣,),
故选:D.
【点评】此题重点考查图形与坐标、菱形的性质、等腰直角三角形的判定与性质、勾股定理等知识,正确地作出辅助线是解题的关键.
二.填空题(共2小题)
2.在一个不透明的布袋中装有黄、白两种颜色的球,除颜色外其他都相同.从袋中随机取出一个球是黄球的概率为0.4,若袋中有12个白球,则布袋中黄球可能有 8 个.
【分析】布袋中黄球可能有x个,根据概率公式列出算式,再进行求解,即可得出答案.
【解答】解:布袋中黄球可能有x个,根据题意得:
=0.4,
解得:x=8,
经检验x=8是原方程的解,
答:布袋中黄球可能有8个.
故答案为:8.
【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率P(A)=.
3.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 ﹣6 .
【分析】依据题意,现将y=x2﹣2x+k变形为y=(x﹣1)2+k﹣1,然后结合﹣3≤x≤2判断当x=﹣3时取最大值,从而列方程计算可以得解.
【解答】解:由题意,∵y=x2﹣2x+k=x2﹣2x+1+k﹣1=(x﹣1)2+k﹣1,
∴抛物线的对称轴是直线x=1.
又∵﹣3≤x≤2,抛物线开口向上,
∴当x=﹣3时,y取最大值,最大值y=16+k﹣1=15+k.
又此时y的最大值为9,
∴15+k=9.
∴k=﹣6.
故答案为:﹣6.
【点评】本题主要考查了二次函数的性质,解题时要熟练掌握并能灵活运用顶点式是关键.
三.解答题(共2小题)
4.综合与实践:如何称量一个空矿泉水瓶的重量?
素材1:如图是一架自制天平,支点O固定不变,左侧托盘固定在点A处,右侧托盘的点P可以在横梁BC段滑动.已知OA=OC=12cm,BC=28cm,一个100g的砝码.
素材2:由于一个空的矿泉水瓶太轻无法称量,小组进行如下操作:左侧托盘放置砝码,右侧托盘滑动点P至点B,空瓶中加入适量的水使天平平衡,再向瓶中加入等量的水,发现点P移动到PC长12cm时,天平平衡.
链接:根据杠杆原理,平衡时:左盘砝码重量×OA=右盘物体重量×OP.(不计托盘与横梁重量)
任务1:设右侧托盘放置y(g)物体,OP长x(cm),求y关于x的函数表达式,并求出y的取值范围.
任务2:求这个空矿泉水瓶的重量.
【分析】任务1:根据左盘砝码重量×OA=右盘物体重量×OP,把相关数值代入后整理可得y与x的关系式,根据OP也就是x的取值范围可得y的取值范围;
任务2:设空瓶的质量为a g,两次加水的质量均为b g,根据左盘砝码重量×OA=右盘物体重量×OP列出二元一次方程组求解即可得到空瓶的质量.
【解答】解:任务1:∵左盘砝码重量×OA=右盘物体重量×OP,右侧托盘放置y(g)物体,OP长x(cm),砝码的质量是100g,OA=12cm,
∴100×12=xy.
∴y=.
∵OC=12cm,BC=28cm,
∴OB=40cm.
∵点P可以在横梁BC段滑动,
∴12≤OP≤40.
即12≤x≤40.
∴30≤y≤100.
答:y关于x的函数表达式为:y=(30≤y≤100);
任务2:设空瓶的重量为a g,两次加水的重量均为b g,根据题意,得:
.
解得:.
答:这个空矿泉水瓶的重量为10 g.
【点评】本题考查反比例函数的应用.根据杠杆平衡的条件找到相等关系并合理使用是解决本题的关键.
5.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
【分析】(1)依据题意,求出Δ=b2﹣4a(﹣4a)=b2+16a2,进而结合a≠0可以判断Δ>0,即可求解;
(2)依据题意,也有对称轴为直线x=2,可得b=﹣4a,从而y=ax2+bx﹣4a=ax2﹣4ax﹣4a,当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,然后计算即可求解;
(3)依据题意,由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,则抛物线开口向下,即a<0,进而求解.
【解答】解:(1)由题意得,Δ=b2﹣4a(﹣4a)=b2+16a2,
又a≠0,
∴a2>0.
∴16a2>0.
又对于任意的b都有b2≥0,
∴Δ=b2+16a2>0.
∴函数图象与x轴的交点个数为2.
(2)∵x=2=﹣,
∴b=﹣4a.
∴抛物线表达式为y=ax2+bx﹣4a=ax2﹣4ax﹣4a,
当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,
解得x=6或﹣2,
则x1=﹣2,x2=6.
(3)将(1,2)代入抛物线表达式得:2=a+b﹣4a,则b=3a+2,
∵a<b,故a<3a+2,
∴解得a>﹣1.
∴抛物线的表达式为y=ax2+(3a+2)x﹣4a,
由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,
∴抛物线开口向下,即a<0.
∴函数的对称轴x=﹣=﹣﹣<0,
解得a<﹣,
∴﹣1<a<﹣.
∴﹣3<3a<﹣2.
故﹣1<3a+2<0,即﹣1<b<0.
∴﹣4<3a+b<﹣2.
∴3a+b的取值范围:﹣4<3a+b<﹣2.
【点评】本题主要考查的是抛物线与x轴的交点、函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
