浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 415.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 16:03:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某无盖的四棱台容器,其示意图如图所示(厚度忽略不计),它的俯视图是( )
A. B. C. D.
2.“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
3.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.连结DF并延长交BC于点I,若I是BC中点,则的值为( )
A. B. C. D.
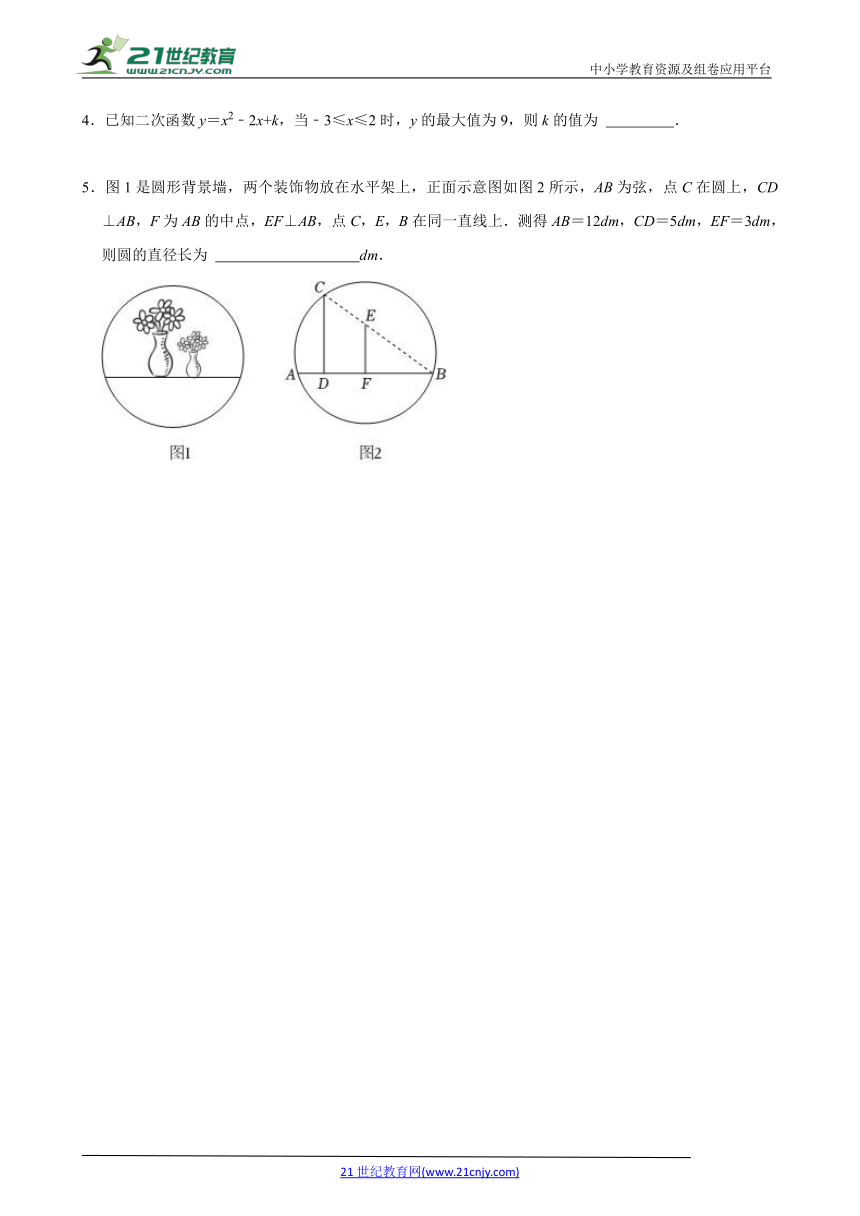
4.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 .
5.图1是圆形背景墙,两个装饰物放在水平架上,正面示意图如图2所示,AB为弦,点C在圆上,CD⊥AB,F为AB的中点,EF⊥AB,点C,E,B在同一直线上.测得AB=12dm,CD=5dm,EF=3dm,则圆的直径长为 dm.
浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
参考答案与试题解析
一.选择题(共3小题)
1.某无盖的四棱台容器,其示意图如图所示(厚度忽略不计),它的俯视图是( )
A. B. C. D.
【分析】根据俯视图是从物体的上面看得到的视图,即可得出答案.
【解答】解:它的俯视图是.
故选:C.
【点评】本题考查简单组合体的三视图,主要考查学生空间想象能力及对立体图形的认知能力.
2.“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
【分析】根据垂直定义可得∠ACB=90°,然后在Rt△ABC中,利用锐角三角函数的定义求出BC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:∵AC⊥BC,
∴∠ACB=90°,
在Rt△ABC中,∠ABC=α,AC=3米,
∴BC==(米),
∵CD=1米,
∴BD=BC﹣CD=(﹣1)米,
∴影长差BD的长为(﹣1)米,
故选:D.
【点评】本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
3.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.连结DF并延长交BC于点I,若I是BC中点,则的值为( )
A. B. C. D.
【分析】设DH=a,AH=b,根据正方形的性质得出AB=BC=CD=AD=,进而利用勾股定理解得即可.
【解答】解:设DH=a,AH=b,根据题意可知:AH=BE=CF=DG=b,DH=CG=BF=AE=a,
∴,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=,
∵I是BC中点,
∴BI=CI=BC=,
在Rt△CDI中,DI2=CD2+CI2,
∴,
整理得:,
∴DI=,
∵四个三角形全等,且四边形EFGH是正方形,
∴DI=DF+FI,
即,
∴,
两边平方得:,
∴,
∴,
令,则,
∴,
解得:x=,
即,
∴,
故选:A.
【点评】此题考查正方形的性质,关键是根据正方形的性质得出AB=BC=CD=AD=解答.
二.填空题(共2小题)
4.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 ﹣6 .
【分析】依据题意,现将y=x2﹣2x+k变形为y=(x﹣1)2+k﹣1,然后结合﹣3≤x≤2判断当x=﹣3时取最大值,从而列方程计算可以得解.
【解答】解:由题意,∵y=x2﹣2x+k=x2﹣2x+1+k﹣1=(x﹣1)2+k﹣1,
∴抛物线的对称轴是直线x=1.
又∵﹣3≤x≤2,抛物线开口向上,
∴当x=﹣3时,y取最大值,最大值y=16+k﹣1=15+k.
又此时y的最大值为9,
∴15+k=9.
∴k=﹣6.
故答案为:﹣6.
【点评】本题主要考查了二次函数的性质,解题时要熟练掌握并能灵活运用顶点式是关键.
5.图1是圆形背景墙,两个装饰物放在水平架上,正面示意图如图2所示,AB为弦,点C在圆上,CD⊥AB,F为AB的中点,EF⊥AB,点C,E,B在同一直线上.测得AB=12dm,CD=5dm,EF=3dm,则圆的直径长为 dm.
【分析】过点C作圆的直径CM,连接AM,证△BEF∽△BCD相似得BD=10dm,则AD=AB﹣BD=2dm,然后由勾股定理求出AC=,BC=,则sin∠ABC==,sinM==,再根据∠ABC=∠M得=,据此可求出该圆的直径.
【解答】解:过点C作圆的直径CM,连接AM,如图所示:
则∠CAM=90°,
∵弦AB=12dm,点F为AB的中点,
∴BF=1/2AB=6dm,
∵CD⊥AB,EF⊥AB,CD=5dm,EF=3dm,
∴EF∥CD,
∴△BEF∽△BCD,
∴BF:BD=EF:CD,
即6:BD=3:5,
∴BD=10dm,
∴AD=AB﹣BD=2dm,
在Rt△ACD中,由勾股定理得:AC==,
在Rt△BCD中,由勾股定理得:BC==,
∴sin∠ABC===,
在Rt△ACM中,sinM==,
∵∠ABC=∠M,
∴=,
∴CM=(dm).
∴该圆的直径为dm.
故答案为:.
【点评】此题主要考查了圆周角定理,勾股定理,相似三角形的判定和性质,熟练掌握圆周角定理,相似三角形的判定和性质,灵活运用勾股定理进行计算是解决问题的关键.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某无盖的四棱台容器,其示意图如图所示(厚度忽略不计),它的俯视图是( )
A. B. C. D.
2.“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
3.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.连结DF并延长交BC于点I,若I是BC中点,则的值为( )
A. B. C. D.
4.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 .
5.图1是圆形背景墙,两个装饰物放在水平架上,正面示意图如图2所示,AB为弦,点C在圆上,CD⊥AB,F为AB的中点,EF⊥AB,点C,E,B在同一直线上.测得AB=12dm,CD=5dm,EF=3dm,则圆的直径长为 dm.
浙江省中考数学考前冲刺每日一练42(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
参考答案与试题解析
一.选择题(共3小题)
1.某无盖的四棱台容器,其示意图如图所示(厚度忽略不计),它的俯视图是( )
A. B. C. D.
【分析】根据俯视图是从物体的上面看得到的视图,即可得出答案.
【解答】解:它的俯视图是.
故选:C.
【点评】本题考查简单组合体的三视图,主要考查学生空间想象能力及对立体图形的认知能力.
2.“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
【分析】根据垂直定义可得∠ACB=90°,然后在Rt△ABC中,利用锐角三角函数的定义求出BC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:∵AC⊥BC,
∴∠ACB=90°,
在Rt△ABC中,∠ABC=α,AC=3米,
∴BC==(米),
∵CD=1米,
∴BD=BC﹣CD=(﹣1)米,
∴影长差BD的长为(﹣1)米,
故选:D.
【点评】本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
3.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.连结DF并延长交BC于点I,若I是BC中点,则的值为( )
A. B. C. D.
【分析】设DH=a,AH=b,根据正方形的性质得出AB=BC=CD=AD=,进而利用勾股定理解得即可.
【解答】解:设DH=a,AH=b,根据题意可知:AH=BE=CF=DG=b,DH=CG=BF=AE=a,
∴,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=,
∵I是BC中点,
∴BI=CI=BC=,
在Rt△CDI中,DI2=CD2+CI2,
∴,
整理得:,
∴DI=,
∵四个三角形全等,且四边形EFGH是正方形,
∴DI=DF+FI,
即,
∴,
两边平方得:,
∴,
∴,
令,则,
∴,
解得:x=,
即,
∴,
故选:A.
【点评】此题考查正方形的性质,关键是根据正方形的性质得出AB=BC=CD=AD=解答.
二.填空题(共2小题)
4.已知二次函数y=x2﹣2x+k,当﹣3≤x≤2时,y的最大值为9,则k的值为 ﹣6 .
【分析】依据题意,现将y=x2﹣2x+k变形为y=(x﹣1)2+k﹣1,然后结合﹣3≤x≤2判断当x=﹣3时取最大值,从而列方程计算可以得解.
【解答】解:由题意,∵y=x2﹣2x+k=x2﹣2x+1+k﹣1=(x﹣1)2+k﹣1,
∴抛物线的对称轴是直线x=1.
又∵﹣3≤x≤2,抛物线开口向上,
∴当x=﹣3时,y取最大值,最大值y=16+k﹣1=15+k.
又此时y的最大值为9,
∴15+k=9.
∴k=﹣6.
故答案为:﹣6.
【点评】本题主要考查了二次函数的性质,解题时要熟练掌握并能灵活运用顶点式是关键.
5.图1是圆形背景墙,两个装饰物放在水平架上,正面示意图如图2所示,AB为弦,点C在圆上,CD⊥AB,F为AB的中点,EF⊥AB,点C,E,B在同一直线上.测得AB=12dm,CD=5dm,EF=3dm,则圆的直径长为 dm.
【分析】过点C作圆的直径CM,连接AM,证△BEF∽△BCD相似得BD=10dm,则AD=AB﹣BD=2dm,然后由勾股定理求出AC=,BC=,则sin∠ABC==,sinM==,再根据∠ABC=∠M得=,据此可求出该圆的直径.
【解答】解:过点C作圆的直径CM,连接AM,如图所示:
则∠CAM=90°,
∵弦AB=12dm,点F为AB的中点,
∴BF=1/2AB=6dm,
∵CD⊥AB,EF⊥AB,CD=5dm,EF=3dm,
∴EF∥CD,
∴△BEF∽△BCD,
∴BF:BD=EF:CD,
即6:BD=3:5,
∴BD=10dm,
∴AD=AB﹣BD=2dm,
在Rt△ACD中,由勾股定理得:AC==,
在Rt△BCD中,由勾股定理得:BC==,
∴sin∠ABC===,
在Rt△ACM中,sinM==,
∵∠ABC=∠M,
∴=,
∴CM=(dm).
∴该圆的直径为dm.
故答案为:.
【点评】此题主要考查了圆周角定理,勾股定理,相似三角形的判定和性质,熟练掌握圆周角定理,相似三角形的判定和性质,灵活运用勾股定理进行计算是解决问题的关键.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
