9.2.1 分式的运算----- 分式的乘除(1) 课件(共21张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 9.2.1 分式的运算----- 分式的乘除(1) 课件(共21张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 945.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:51:20 | ||
图片预览







文档简介
(共21张PPT)
第9章 分 式
9.2 分式的运算
9.2.1 分式的乘除(1)
学习目标
1.理解并掌握分式的乘除运算法则,能运用其进行运算并解决实际问题.(重点)
2.能够进行分子、分母为多项式的分式乘除法运算.(难点)
回顾旧知
1.分式的约分
2.最简分式
根据分式的基本性质,把一个分式的分子和分母的公因式约去叫做分式的约分.
像,,这样,分子与分母只有公因式1的分式,叫做最简分式.约分通常是把分式化成最简分式或者整式.
1.你还记得分数的乘除运算吗?
思 考
(1)×=_________;
(2)×(=_________;
(3)÷(=_________;
(4)÷=_________.
×=
×(=
÷(
÷=
1.你还记得分数的乘除运算吗?
分数乘分数,用分子的积作为积的分子,分母的积作为积的分母;
分数除以分数,把除数的分子、分母颠倒位置后,与被除数相乘.
思 考
(1)×=_________;
(2)×(=_________;
(3)÷(=_________;
(4)÷=_________.
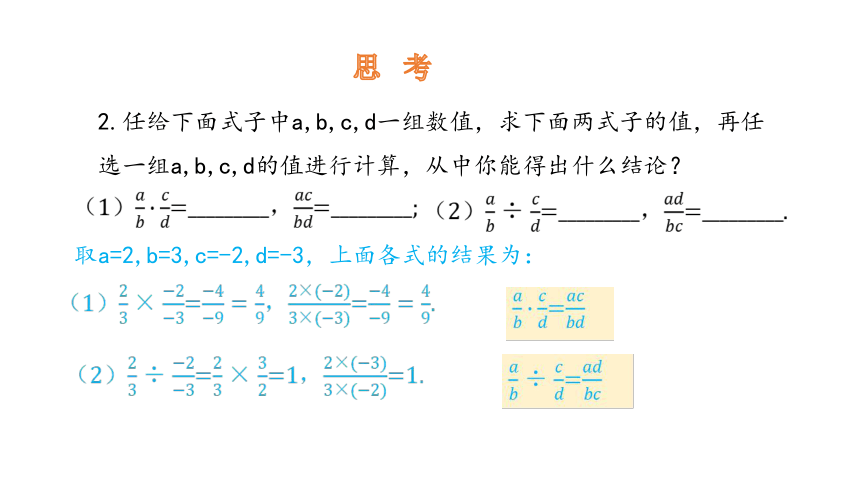
2.任给下面式子中a,b,c,d一组数值,求下面两式子的值,再任选一组a,b,c,d的值进行计算,从中你能得出什么结论?
思 考
(1)=_________,=_________;
(2)=_________,=_________.
取a=2,b=3,c=-2,d=-3,上面各式的结果为:
(1)=,=.
(2)==1,=1.
=
=
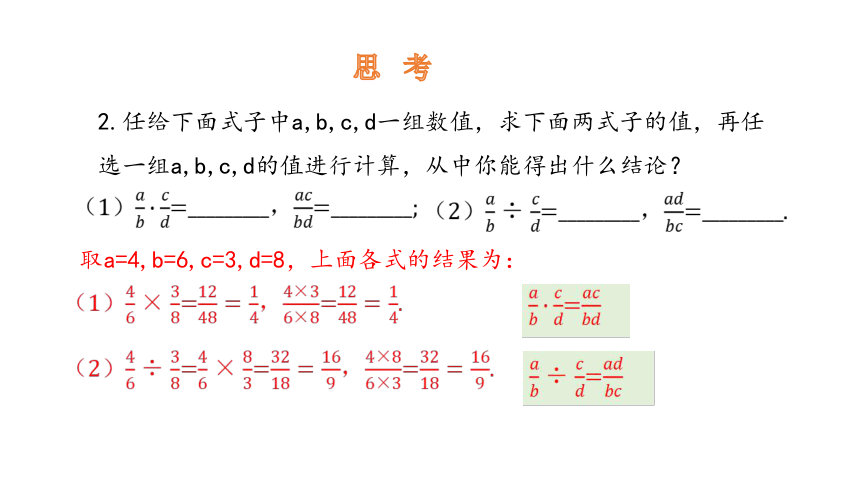
2.任给下面式子中a,b,c,d一组数值,求下面两式子的值,再任选一组a,b,c,d的值进行计算,从中你能得出什么结论?
思 考
(1)=_________,=_________;
(2)=_________,=_________.
取a=4,b=6,c=3,d=8,上面各式的结果为:
(1)=,=.
(2)==,=.
=
=
与分数乘除类似,分式乘除的法则为:
乘法法则:两个分式相乘,用分子的积作积的分子,用分母的积作积的分母.
除法法则:两个分式相除,将除式的分子、分母颠倒位置后,与被除式相乘.
讲授新课
教材例题
例1 计算:
(1); (2).
解:
=
=.
解:
=
=.
教材例题
例2 计算:.
解:
=
=
=
=.
解:原式=
=··
=.
先约分后相乘可使运算简化.
例1 计算:
解:
先把除法转化为乘法.
约分
注意:按照法则进行分式乘除运算,如果运算结果不是最简分式,一定要进行约分,使运算结果化成最简分式.
例题解读
解:(1)原式
(2)原式
(1)
(2)
小试牛刀
例题解读
例2 计算:
解:原式=
分子、分母是多项式时,通常先分解因式,再约分.
约分
例题解读
解:原式=
先把除法转化为乘法.
整式与分式运算时,可以把整式看成分母是1的式.
注意负号.
例2 计算:
例题解读
小试牛刀
(1)
解:原式
例题解读
解:原式
(2)
随堂小测
1. 下列计算对吗?若不对,要怎样改正?
对
2. 计算 等于( )
A. B. C. D.
C
3. 化简 的结果是( )
B
随堂小测
4. 化简: .
解:原式=
先分解因式,再利用分式的乘法法则,结果要化成最简分式或整式.
随堂小测
解:
5. 计算:
原式
随堂小测
分式乘除运算
乘除法运算
注意
(1)分子分母是单项式的,先按法则进行,再约分化成最简分式或整式
除法先转化成乘法,再按照乘法法则进行运算
(2)分子分母是多项式的,通常要先分解因式再按法则进行
(3)运用法则时要注意符号的变化
课时小结
1.分式的分子、分母都是几个因式的积的形式,可先约去分子、分母的公因式,再按照法则进行计算.
2.分子或分母是多项式的按以下方法进行:
①将原分式中含同一字母的各多项式按降幂(或升幂)排列;在乘除过程中遇到整式则视其为分母为1,分子为这个整式的分式;
②把各分式中分子或分母里的多项式分解因式;
③应用分式乘除法法则进行运算.(注意:结果为最简分式或整式.)
分式乘除法的解题步骤
课时小结
第9章 分 式
9.2 分式的运算
9.2.1 分式的乘除(1)
学习目标
1.理解并掌握分式的乘除运算法则,能运用其进行运算并解决实际问题.(重点)
2.能够进行分子、分母为多项式的分式乘除法运算.(难点)
回顾旧知
1.分式的约分
2.最简分式
根据分式的基本性质,把一个分式的分子和分母的公因式约去叫做分式的约分.
像,,这样,分子与分母只有公因式1的分式,叫做最简分式.约分通常是把分式化成最简分式或者整式.
1.你还记得分数的乘除运算吗?
思 考
(1)×=_________;
(2)×(=_________;
(3)÷(=_________;
(4)÷=_________.
×=
×(=
÷(
÷=
1.你还记得分数的乘除运算吗?
分数乘分数,用分子的积作为积的分子,分母的积作为积的分母;
分数除以分数,把除数的分子、分母颠倒位置后,与被除数相乘.
思 考
(1)×=_________;
(2)×(=_________;
(3)÷(=_________;
(4)÷=_________.
2.任给下面式子中a,b,c,d一组数值,求下面两式子的值,再任选一组a,b,c,d的值进行计算,从中你能得出什么结论?
思 考
(1)=_________,=_________;
(2)=_________,=_________.
取a=2,b=3,c=-2,d=-3,上面各式的结果为:
(1)=,=.
(2)==1,=1.
=
=
2.任给下面式子中a,b,c,d一组数值,求下面两式子的值,再任选一组a,b,c,d的值进行计算,从中你能得出什么结论?
思 考
(1)=_________,=_________;
(2)=_________,=_________.
取a=4,b=6,c=3,d=8,上面各式的结果为:
(1)=,=.
(2)==,=.
=
=
与分数乘除类似,分式乘除的法则为:
乘法法则:两个分式相乘,用分子的积作积的分子,用分母的积作积的分母.
除法法则:两个分式相除,将除式的分子、分母颠倒位置后,与被除式相乘.
讲授新课
教材例题
例1 计算:
(1); (2).
解:
=
=.
解:
=
=.
教材例题
例2 计算:.
解:
=
=
=
=.
解:原式=
=··
=.
先约分后相乘可使运算简化.
例1 计算:
解:
先把除法转化为乘法.
约分
注意:按照法则进行分式乘除运算,如果运算结果不是最简分式,一定要进行约分,使运算结果化成最简分式.
例题解读
解:(1)原式
(2)原式
(1)
(2)
小试牛刀
例题解读
例2 计算:
解:原式=
分子、分母是多项式时,通常先分解因式,再约分.
约分
例题解读
解:原式=
先把除法转化为乘法.
整式与分式运算时,可以把整式看成分母是1的式.
注意负号.
例2 计算:
例题解读
小试牛刀
(1)
解:原式
例题解读
解:原式
(2)
随堂小测
1. 下列计算对吗?若不对,要怎样改正?
对
2. 计算 等于( )
A. B. C. D.
C
3. 化简 的结果是( )
B
随堂小测
4. 化简: .
解:原式=
先分解因式,再利用分式的乘法法则,结果要化成最简分式或整式.
随堂小测
解:
5. 计算:
原式
随堂小测
分式乘除运算
乘除法运算
注意
(1)分子分母是单项式的,先按法则进行,再约分化成最简分式或整式
除法先转化成乘法,再按照乘法法则进行运算
(2)分子分母是多项式的,通常要先分解因式再按法则进行
(3)运用法则时要注意符号的变化
课时小结
1.分式的分子、分母都是几个因式的积的形式,可先约去分子、分母的公因式,再按照法则进行计算.
2.分子或分母是多项式的按以下方法进行:
①将原分式中含同一字母的各多项式按降幂(或升幂)排列;在乘除过程中遇到整式则视其为分母为1,分子为这个整式的分式;
②把各分式中分子或分母里的多项式分解因式;
③应用分式乘除法法则进行运算.(注意:结果为最简分式或整式.)
分式乘除法的解题步骤
课时小结
