9.2.2(1) 分式的加减-----(第1课时 通分) 课件 (共14张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 9.2.2(1) 分式的加减-----(第1课时 通分) 课件 (共14张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 790.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第九章 分 式
9.2 分式的运算
9.2.2 分式的加减
学习目标
1.了解并掌握通分、最简公分母的概念.
2. 会找分式的最简公分母.(重点、难点)
情境引入
你还记得异分母的分数如何加减吗?
异分母分数相加减,先通分,化为同分母分数后,再加减.
你认为异分母的分式应该如何加减 比如
应该怎样计算?
讲授新课
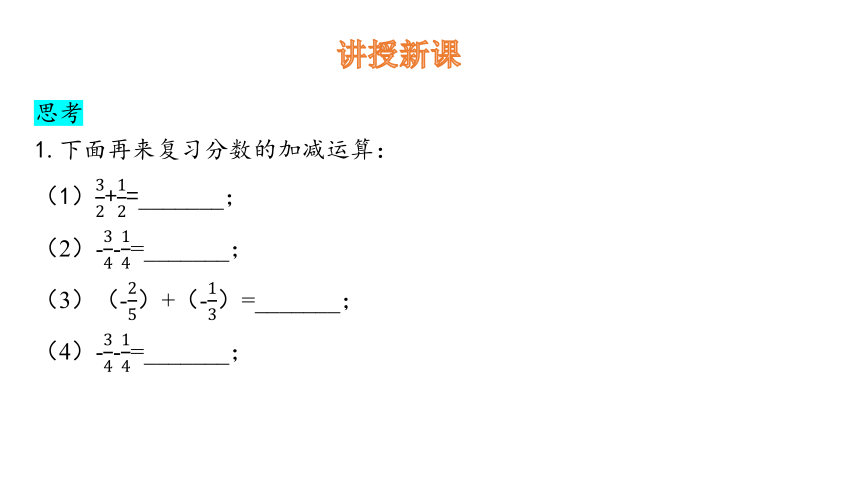
思考
1.下面再来复习分数的加减运算:
(1)+=_______;
(2)--=_______;
(3)(-)+(-)=_______;
(4)--=_______;
讲授新课
思考
2.类比分数的加减运算,下面分式的加减运算如何进行?
(1)+;
(2)-;
(3)
(4)--
讲授新课
与分数类似,在计算异分母分式的加减时,要利用分式的基本性质,先把分母不相同的分式化成分母相同的分式,再进行加减.化异分母的分式为同分母的分式的过程,叫做分式的通分.
教材例题
例 通分:
(1),,;
解:(1)3a b,4ab ,12ab中系数的最小公倍数为12,字母a的最高次幂为a ,字母b的最高次幂为b ,故公分母为12a b ,
通分后分别为:=,
=,
.
教材例题
例 通分:
(2),,.
解:(2)x -y =(x-y)(x+y),
x +2xy+y =(x+y) ,
x +xy+y =x(x+y),
故公分母为x(x+y) (x-y).
通分后分别为:=
=
=.
新课讲授
异分母分式通分时,关键是确定公分母.通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫作最简公分母.
讲授新课
在求最简公分母时应注意:
(1)如果各分母的系数都是整数时,通常取它们系数的最小公倍数作为最简公分母的系数;
(2)当分母是多项式时,一般应先分解因式.
例题解读
(1) 的最简公分母是______________
(2) 的最简公分母是______________________
(3) 的最简公分母是_________________
例1 做一做:找最简公分母
例2 将下列各组分式通分:
解:
解:
解:
随 堂 小 测
解:
最简公分母是
通分:
解:
最简公分母是
(x-5)(x+5)
课堂小结
2.确定最简分式的最简公分母的一般思路:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
1.化异分母分式为同分母分式的过程,叫做分式的通分.
第九章 分 式
9.2 分式的运算
9.2.2 分式的加减
学习目标
1.了解并掌握通分、最简公分母的概念.
2. 会找分式的最简公分母.(重点、难点)
情境引入
你还记得异分母的分数如何加减吗?
异分母分数相加减,先通分,化为同分母分数后,再加减.
你认为异分母的分式应该如何加减 比如
应该怎样计算?
讲授新课
思考
1.下面再来复习分数的加减运算:
(1)+=_______;
(2)--=_______;
(3)(-)+(-)=_______;
(4)--=_______;
讲授新课
思考
2.类比分数的加减运算,下面分式的加减运算如何进行?
(1)+;
(2)-;
(3)
(4)--
讲授新课
与分数类似,在计算异分母分式的加减时,要利用分式的基本性质,先把分母不相同的分式化成分母相同的分式,再进行加减.化异分母的分式为同分母的分式的过程,叫做分式的通分.
教材例题
例 通分:
(1),,;
解:(1)3a b,4ab ,12ab中系数的最小公倍数为12,字母a的最高次幂为a ,字母b的最高次幂为b ,故公分母为12a b ,
通分后分别为:=,
=,
.
教材例题
例 通分:
(2),,.
解:(2)x -y =(x-y)(x+y),
x +2xy+y =(x+y) ,
x +xy+y =x(x+y),
故公分母为x(x+y) (x-y).
通分后分别为:=
=
=.
新课讲授
异分母分式通分时,关键是确定公分母.通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫作最简公分母.
讲授新课
在求最简公分母时应注意:
(1)如果各分母的系数都是整数时,通常取它们系数的最小公倍数作为最简公分母的系数;
(2)当分母是多项式时,一般应先分解因式.
例题解读
(1) 的最简公分母是______________
(2) 的最简公分母是______________________
(3) 的最简公分母是_________________
例1 做一做:找最简公分母
例2 将下列各组分式通分:
解:
解:
解:
随 堂 小 测
解:
最简公分母是
通分:
解:
最简公分母是
(x-5)(x+5)
课堂小结
2.确定最简分式的最简公分母的一般思路:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
1.化异分母分式为同分母分式的过程,叫做分式的通分.
